【xsy1232】Magic 最小割

题目大意：给你一个$n$个点，$m$条有向边的图，每个点有一个点权$a_i$，同时你可以用$b_i$的代价将$a_i$变为$0$

另外你要付出$\sum\limits_{i=1}^n\max\limits_{(i,j)}a_j$这么多代价。请最小化代价。

数据范围：$n≤1000$，$m≤50000$。

貌似是一道套路最小割

把每个点拆成两个点，对每条边新建一个点，将一个点的出边按终点的$a$从大到小排序后建图如下

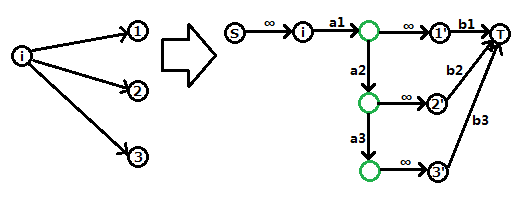
该建图方式，只有让某个前缀$a_i$全部变为$0$，一个点产生的费用才会改变，这个建图保证了如果要割$a_i$就必须要割掉$b_1$至$b_{i-1}$，且不会割掉两个$a$

我们对每个点都这么建一波，然后跑个最大流就没了

orzlyy！！！！！

 #include<bits/stdc++.h>
 #define M 60005
 #define INF (1<<30)
 using namespace std;

 struct edge{int u,v,next;}e[M*]={}; int head[M]={},use=;
 void add(int x,int y,int z){e[use].u=y;e[use].v=z;e[use].next=head[x];head[x]=use++;}
 void Add(int x,int y,int z){add(x,y,z); add(y,x,);}
 int dis[M]={},S,T; queue<int> q;
 bool bfs(){
     memset(dis,,sizeof(dis));
     dis[S]=; q.push(S);
     while(!q.empty()){
         int u=q.front(); q.pop();
         for(int i=head[u];~i;i=e[i].next)
         if(dis[e[i].u]==&&e[i].v){
             dis[e[i].u]=dis[u]+;
             q.push(e[i].u);
         }
     }
     return dis[T];
 }
 int dfs(int x,int flow){
     if(x==T) return flow; int sum=;
     for(int i=head[x];~i;i=e[i].next)
     if(dis[x]+==dis[e[i].u]&&e[i].v){
         int k=dfs(e[i].u,min(flow,e[i].v));
         sum+=k; flow-=k;
         e[i].v-=k; e[i^].v+=k;
         if(flow==) return sum;
     }
     if(sum==) dis[x]=-;
     return sum;
 }
 int dinic(){
     int res=;
     while(bfs())
     res+=dfs(S,INF);
     return res;
 }

 int n,m,a[M]={},b[M]={};
 vector<int> g[M];
 bool cmp(int x,int y){return a[x]>a[y];}
 void ReadData(){
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%d",a+i);
     for(int i=;i<=n;i++) scanf("%d",b+i);
     for(int i=;i<=m;i++){
         int x,y; scanf("%d%d",&x,&y);
         g[x].push_back(y);// g[y].push_back(x);
     }
 }
 void build(){
     S=; T=*n+; int N=*n+;
     for(int i=;i<=n;i++) Add(S,i,INF);
     for(int i=;i<=n;i++) Add(i+n,T,b[i]);
     for(int x=;x<=n;x++){
         sort(g[x].begin(),g[x].end(),cmp);
         for(int i=;i<g[x].size();i++){
             N++;
             Add(i?N-:x,N,a[g[x][i]]);
             Add(N,n+g[x][i],INF);
         }
     }
 }
 int main(){
     ReadData();
     build();
     cout<<dinic()<<endl;
 }