在上一篇文章《数据准备<4>：变量筛选-理论篇》中，我们介绍了变量筛选的三种方法：基于经验的方法、基于统计的方法和基于机器学习的方法，本文将介绍后两种方法在Python（sklearn）环境下的具体实现。

1.环境介绍

版本：python2.7

工具：Spyder

开发人：hbsygfz

2.数据集介绍

数据集：sklearn中自带的cancer数据集，可参考官方介绍

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()

data = cancer.data

feature_names = cancer.feature_names

target = cancer.target

target_names = cancer.target_names

print("数据集大小:{}".format(data.shape))

print("特征:{}".format(feature_names))

print("目标变量:{}".format(target_names))

Out[1]:

数据集大小:(569, 30)

特征:['mean radius' 'mean texture' 'mean perimeter' 'mean area'

 'mean smoothness' 'mean compactness' 'mean concavity'

 'mean concave points' 'mean symmetry' 'mean fractal dimension'

 'radius error' 'texture error' 'perimeter error' 'area error'

 'smoothness error' 'compactness error' 'concavity error'

 'concave points error' 'symmetry error' 'fractal dimension error'

 'worst radius' 'worst texture' 'worst perimeter' 'worst area'

 'worst smoothness' 'worst compactness' 'worst concavity'

 'worst concave points' 'worst symmetry' 'worst fractal dimension']

目标变量:['malignant' 'benign']

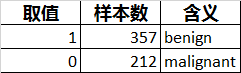
由上可知，cancer数据集是一个(569,30)大小的数据集，共有30个特征，569条样本，目标变量为二分类，取值分别为'malignant'和'benign'。

从数据上看，发现这30个特征均为连续型数据。结合官方介绍，了解到目标变量的分布及含义如下：

3.代码实现

3.1 基于统计的方法

（0）准备工作

## 1.数据集导入

dataDf = pd.DataFrame(data,columns=list(feature_names))

targetSer = pd.Series(target)

targetSer.name = 'is_benign'

dataset = pd.concat([dataDf,targetSer],axis=1) #合并特征数据和目标变量数据

discreteColList = []        #离散型变量

continuousColList = list(feature_names)     #连续型变量

targetCol = 'is_benign'     #目标变量

## 2.数据预处理

# 定义连续变量分箱函数

def binCreate(df,bins):

    colList = df.columns

    resDf = pd.DataFrame(columns=colList)

    m,n = df.shape

    referSer = pd.Series(range(m))

    referSer.name = 'rank'

    lableSer = pd.qcut(referSer, bins, labels=range(bins))

    lableSer.name = 'bin'

    lableDF = pd.concat([referSer,lableSer], axis=1)  #顺序与箱号合并

    for col in colList:

        rankSer = df[col].rank(method='min')

        rankSer.name = 'rank'

        rankDF = pd.concat([df[col],rankSer], axis=1)

        binsDF = pd.merge(rankDF, lableDF, on='rank', how='left')

        resDf[col] = binsDF['bin']

    return resDf

# 定义区间(类别)分布统计函数

def binDistStatistic(df,tag):

    colList = list(df.columns)  #转成列表

    colList.remove(tag)         #删除目标变量

    resDf = pd.DataFrame(columns=['colName','bin','binAllCnt','binPosCnt','binNegCnt','binPosRto','binNegRto'])

    for col in colList:

        allSer = df.groupby(col)[tag].count()         #计算样本数

        allSer = allSer[allSer>0]                     #剔除无效区间

        allSer.name = 'binAllCnt'                     #定义列名

        posSer = df.groupby(col)[tag].sum()           #计算正样本数

        posSer = posSer[allSer.index]                 #剔除无效区间

        posSer.name = 'binPosCnt'                     #定义列名

        tmpDf = pd.concat([allSer,posSer], axis=1)    #合并统计结果

        tmpDf = tmpDf.reset_index()                   #行索引转为一列

        tmpDf = tmpDf.rename(columns={col:'bin'})    #修改区间列列名

        tmpDf['colName'] = col                        #增加字段名称列

        tmpDf['binNegCnt'] = tmpDf['binAllCnt'] - tmpDf['binPosCnt']             #计算负样本数

        tmpDf['binPosRto'] = tmpDf['binPosCnt'] * 1.0000 / tmpDf['binAllCnt']    #计算正样本比例

        tmpDf['binNegRto'] = tmpDf['binNegCnt'] * 1.0000 / tmpDf['binAllCnt']    #计算负样本比例

        tmpDf = tmpDf.reindex(columns=['colName','bin','binAllCnt','binPosCnt','binNegCnt','binPosRto','binNegRto'])  #索引重排

        resDf = pd.concat([resDf,tmpDf])      #结果追加

    rows, cols = df.shape

    posCnt = df[tag].sum()

    resDf['allCnt'] = rows                              #总体样本数

    resDf['posCnt'] = posCnt                            #总体正样本数

    resDf['negCnt'] = rows - posCnt                     #总体负样本数

    resDf['posRto'] = posCnt * 1.0000 / rows            #总体正样本比例

    resDf['negRto'] = (rows - posCnt) * 1.0000 / rows   #总体负样本比例

    resDf['binPosCov'] = resDf['binPosCnt'] / resDf['posCnt']

    resDf['binNegCov'] = resDf['binNegCnt'] / resDf['negCnt']

    return resDf

# 定义区间(类别)属性统计函数

def binAttrStatistic(df,cont,disc,bins):

    m,n = df.shape

    referSer = pd.Series(range(m))

    referSer.name = 'rank'

    lableSer = pd.qcut(referSer, bins, labels=range(bins))

    lableSer.name = 'bin'

    lableDF = pd.concat([referSer,lableSer], axis=1)  #顺序与箱号合并

    resDf = pd.DataFrame(columns=['colName','bin','minVal','maxVal','binInterval'])

    for col in cont:

        rankSer = df[col].rank(method='min')

        rankSer.name = 'rank'

        rankDF = pd.concat([df[col],rankSer], axis=1)

        binsDF = pd.merge(rankDF, lableDF, on='rank', how='left')

        minSer = binsDF.groupby('bin')[col].min()

        minSer.name = 'minVal'

        maxSer = binsDF.groupby('bin')[col].max()

        maxSer.name = 'maxVal'

        tmpDf = pd.concat([minSer,maxSer], axis=1)

        tmpDf = tmpDf.reset_index()

        tmpDf['colName'] = col

        tmpDf['binInterval'] = tmpDf['minVal'].astype('str') + '-' + tmpDf['maxVal'].astype('str')

        tmpDf = tmpDf.reindex(columns=['colName','bin','minVal','maxVal','binInterval'])

        tmpDf = tmpDf[tmpDf['binInterval']!='nan-nan']

        resDf =  pd.concat([resDf,tmpDf])

    for col in disc:

        binSer = pd.Series(df[col].unique())

        tmpDf = pd.concat([binSer,binSer], axis=1)

        tmpDf['colName'] = col

        tmpDf.rename(columns={0:'bin',1:'binInterval'}, inplace = True)

        tmpDf = tmpDf.reindex(columns=['colName','bin','minVal','maxVal','binInterval'])

        resDf = pd.concat([resDf,tmpDf])

    return resDf

# 定义结果合并函数

def binStatistic(df,cont,disc,tag,bins):

    binResDf = binCreate(df[cont], bins)  # 连续变量分箱

    binData = pd.concat([binResDf,df[disc],df[tag]], axis=1)  #合并离散变量与目标变量

    binDistStatResDf = binDistStatistic(binData,tag)  #对分箱后数据集进行分布统计

    binAttrStatResDf = binAttrStatistic(df,cont,disc,bins)  #区间(类别)大小统计

    binStatResDf = pd.merge(binDistStatResDf, binAttrStatResDf, left_on=['colName','bin'], right_on=['colName','bin'], how='left')

    resDf = binStatResDf.reindex(columns=['colName','bin','binInterval','minVal','maxVal','binAllCnt','binPosCnt','binNegCnt','binPosRto','binNegRto','allCnt','posCnt','negCnt','posRto','negRto','binPosCov','binNegCov'])

    return resDf

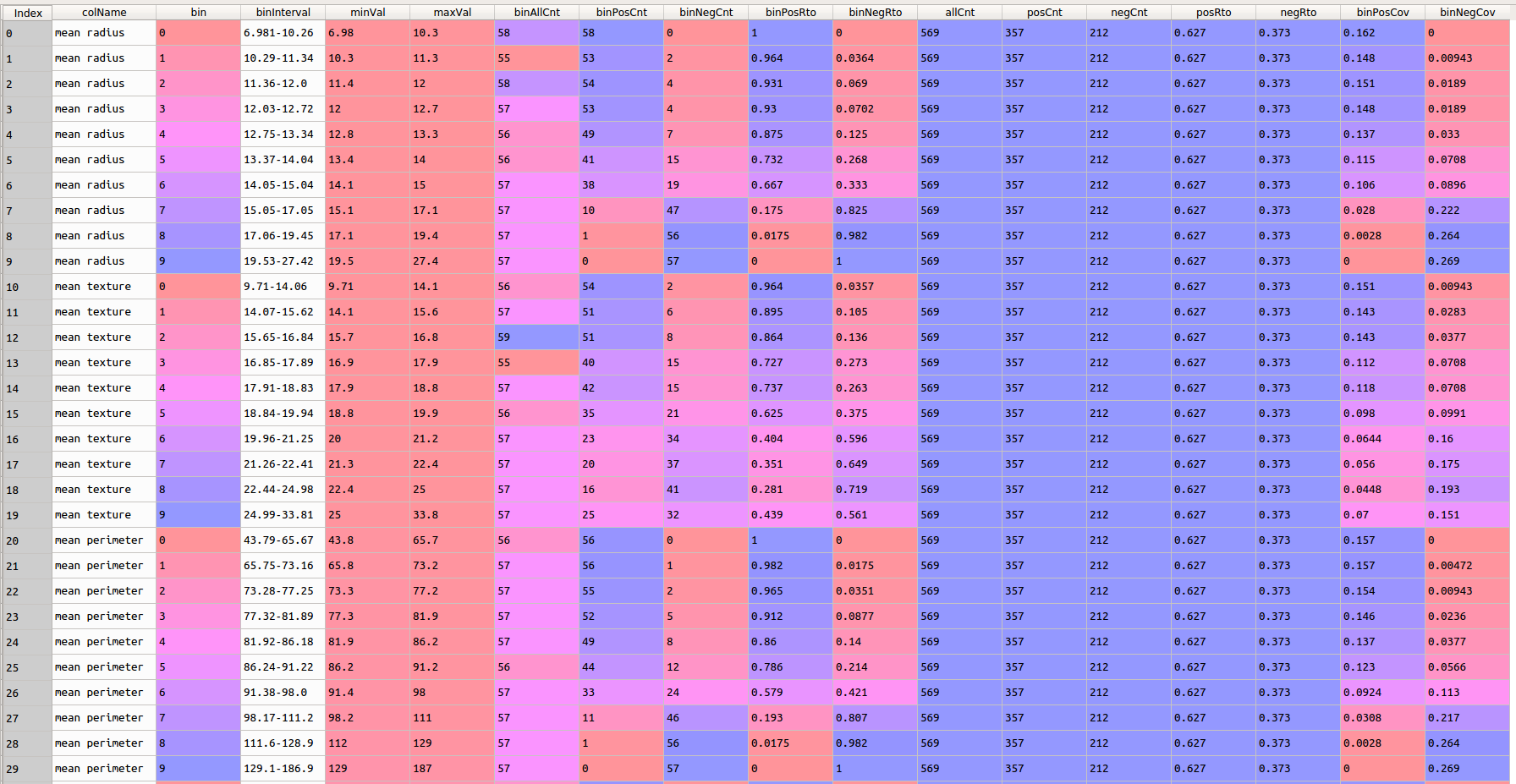
上述代码，首先将数据集中的连续变量进行等频分箱离散化，然后计算各分组中的正、负样本的比例以及占其总体的比例，方便后续预测能力指标的计算。调用：

binStatisticResDf = binStatistic(dataset, continuousColList, discreteColList, targetCol, 10)

结果如下：

（1）信息增益

##信息增益计算

import math

def entropyVal(prob):

    if (prob == 0 or prob == 1):

        entropy = 0

    else:

        entropy = -(prob * math.log(prob,2) + (1-prob) * math.log((1-prob),2))

    return entropy

def gain(df,cont,disc,tag,bins):

    binDf = binStatistic(df,cont,disc,tag,bins)

    binDf['binAllRto'] = binDf['binAllCnt'] / binDf['allCnt']   #计算各区间样本占比

    binDf['binEnty'] = binDf['binAllRto'] * binDf['binPosRto'].apply(entropyVal)    #计算各区间信息熵

    binDf['allEnty'] = binDf['posRto'].apply(entropyVal)        #计算总体信息熵

    tmpSer = binDf['allEnty'].groupby(binDf['colName']).mean() - binDf['binEnty'].groupby(binDf['colName']).sum()   #计算信息增益=总体信息熵-各区间信息熵加权和

    tmpSer.name = 'gain'

    resSer = tmpSer.sort_values(ascending=False)                #按信息增益大小降序重排

    return resSer

gainSer = gain(dataset, continuousColList, discreteColList, targetCol, 10)

结果如下：

gainSer

Out[11]:

colName

worst perimeter            0.684679

worst radius               0.660968

worst area                 0.660008

worst concave points       0.638077

mean concave points        0.624494

mean perimeter             0.560532

mean area                  0.556175

mean radius                0.549344

mean concavity             0.522874

area error                 0.511074

worst concavity            0.463328

radius error               0.365562

perimeter error            0.355755

worst compactness          0.321361

mean compactness           0.312030

concavity error            0.217127

concave points error       0.198744

mean texture               0.187825

worst texture              0.182411

worst smoothness           0.152196

worst symmetry             0.147642

compactness error          0.135060

mean smoothness            0.115767

mean symmetry              0.098459

worst fractal dimension    0.098175

mean fractal dimension     0.042941

fractal dimension error    0.042878

texture error              0.017587

smoothness error           0.016914

symmetry error             0.016343

Name: gain, dtype: float64

（2）基尼指数

##基尼指数计算

def giniVal(prob):

    gini = 1 - pow(prob,2) - pow(1-prob,2)

    return gini

def gini(df,cont,disc,tag,bins):

    binDf = binStatistic(df,cont,disc,tag,bins)

    binDf['binAllRto'] = binDf['binAllCnt'] / binDf['allCnt']   #计算各区间样本占比

    binDf['binGini'] = binDf['binAllRto'] * binDf['binPosRto'].apply(giniVal)    #计算各区间信息熵

    binDf['allGini'] = binDf['posRto'].apply(giniVal)        #计算总体信息熵

    tmpSer = binDf['allGini'].groupby(binDf['colName']).mean() - binDf['binGini'].groupby(binDf['colName']).sum()   #计算信息增益=总体信息熵-各区间信息熵加权和

    tmpSer.name = 'gini'

    resSer = tmpSer.sort_values(ascending=False)                #按信息增益大小降序重排

    return resSer

giniSer = gini(dataset, continuousColList, discreteColList, targetCol, 10)

结果如下：

giniSer

Out[12]:

colName

worst perimeter            0.354895

worst radius               0.342576

worst area                 0.341825

worst concave points       0.335207

mean concave points        0.329700

mean area                  0.301404

mean perimeter             0.300452

mean radius                0.297503

mean concavity             0.289159

area error                 0.276011

worst concavity            0.256282

radius error               0.207248

perimeter error            0.197484

worst compactness          0.184931

mean compactness           0.182082

concavity error            0.118407

concave points error       0.114959

mean texture               0.110607

worst texture              0.106525

worst smoothness           0.092690

worst symmetry             0.091039

compactness error          0.078588

mean smoothness            0.067543

worst fractal dimension    0.061877

mean symmetry              0.059676

mean fractal dimension     0.027288

fractal dimension error    0.026794

texture error              0.010803

smoothness error           0.010417

symmetry error             0.010157

Name: gini, dtype: float64

（3）区分度

##区分度计算

def lift(df,cont,disc,tag,bins):

    binDf = binStatistic(df,cont,disc,tag,bins)

    binDf['binLift'] = binDf['binPosRto'] / binDf['posRto']             #区间提升度=区间正样本比例/总体正样本比例

    tmpSer = binDf['binLift'].groupby(binDf['colName']).max()           #变量区分度=max(区间提升度)

    tmpSer.name = 'lift'

    resSer = tmpSer.sort_values(ascending=False)        #按区分度大小降序重排

    return resSer

liftSer = lift(dataset, continuousColList, discreteColList, targetCol, 10)

结果如下：

liftSer

Out[13]:

colName

area error                 1.593838

mean radius                1.593838

mean concavity             1.593838

perimeter error            1.593838

radius error               1.593838

mean concave points        1.593838

mean area                  1.593838

worst area                 1.593838

concavity error            1.593838

worst concave points       1.593838

worst perimeter            1.593838

worst radius               1.593838

mean perimeter             1.593838

worst concavity            1.565875

mean compactness           1.565376

concave points error       1.536915

compactness error          1.536915

mean texture               1.536915

worst compactness          1.536915

mean smoothness            1.508453

worst texture              1.508453

worst smoothness           1.479992

mean symmetry              1.454027

worst fractal dimension    1.398103

worst symmetry             1.366146

fractal dimension error    1.280762

mean fractal dimension     1.258293

smoothness error           1.230331

texture error              1.223840

symmetry error             1.209118

Name: lift, dtype: float64

（4）信息值(IV)

##信息值(IV)计算

def iv(df,cont,disc,tag,bins):

    binDf = binStatistic(df,cont,disc,tag,bins)

    binDf['binPosCovAdj'] = (binDf['binPosCnt'].replace(0,1)) / binDf['posCnt']     #调整后区间正样本覆盖率(避免值为0无法取对数)

    binDf['binNegCovAdj'] = (binDf['binNegCnt'].replace(0,1)) / binDf['negCnt']     #调整后区间负样本覆盖率(避免值为0无法取对数)

    binDf['woe'] = binDf['binPosCovAdj'].apply(lambda x:math.log(x,math.e)) - binDf['binNegCovAdj'].apply(lambda x:math.log(x,math.e))

    binDf['iv'] = binDf['woe'] * (binDf['binPosCovAdj'] - binDf['binNegCovAdj'])

    tmpSer = binDf.groupby('colName')['iv'].sum()

    tmpSer.name = 'iv'

    resSer = tmpSer.sort_values(ascending=False)

    return resSer

ivSer = iv(dataset, continuousColList, discreteColList, targetCol, 10)

结果如下：

ivSer

Out[14]:

colName

worst perimeter            5.663336

worst area                 5.407202

worst radius               5.391269

worst concave points       5.276160

mean concave points        5.117567

mean perimeter             4.643066

mean area                  4.507951

mean radius                4.460431

area error                 4.170720

mean concavity             3.999623

worst concavity            3.646313

perimeter error            2.777306

radius error               2.694609

worst compactness          2.320652

mean compactness           2.223346

concavity error            1.508040

concave points error       1.368055

mean texture               1.263312

worst texture              1.212502

worst smoothness           0.972226

worst symmetry             0.971215

compactness error          0.916664

mean smoothness            0.772058

mean symmetry              0.617936

worst fractal dimension    0.596305

fractal dimension error    0.253930

mean fractal dimension     0.244841

texture error              0.099411

smoothness error           0.087521

symmetry error             0.083463

Name: iv, dtype: float64

这里，我们对比上述4个指标计算的重要性排序结果。

gainRankSer = gainSer.rank(ascending=False,method='min')    #并列排名取最小排名

giniRankSer = giniSer.rank(ascending=False,method='min')    #并列排名取最小排名

liftRankSer = liftSer.rank(ascending=False,method='min')    #并列排名取最小排名

ivRankSer = ivSer.rank(ascending=False,method='min')        #并列排名取最小排名

resDf = pd.concat([gainRankSer,giniRankSer,liftRankSer,ivRankSer],axis=1)

resDf2 = resDf.sort_values(by='gain',ascending=True)        #使用gain排名进行重排

结果如下：

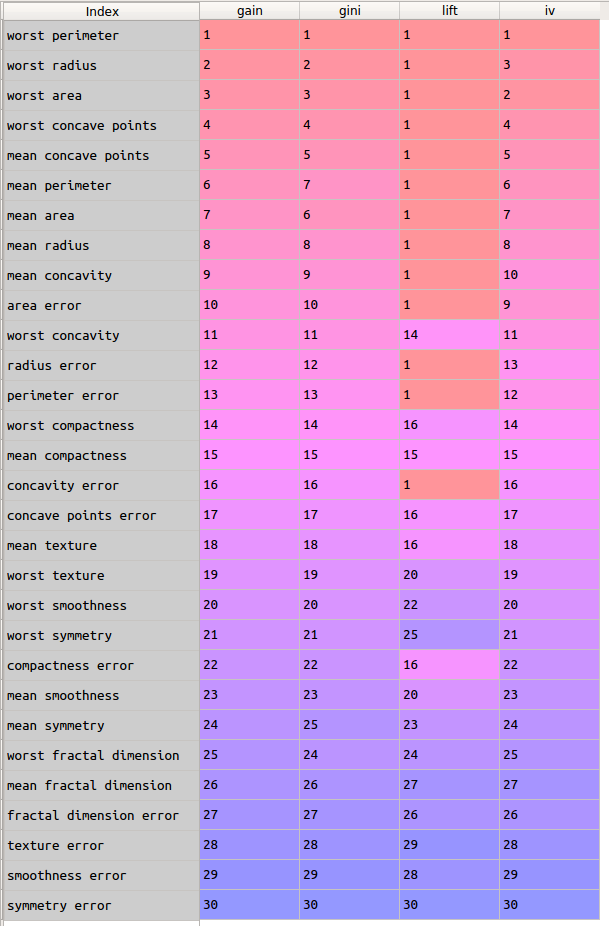
通过颜色深浅，可以很清晰的看到：

1）信息增益、基尼指数降低值的评估结果基本没有差别，二者与信息值(IV)在极个别的特征上有较小的差别；

2）区分度与其他三个指标，整体上差别不大，但是其对部分变量的评估结果相同，不能像其他三个指标那样这些变量的预测能力区分开（如表中预测能力前10名的变量）。

综上所述，在实际工程实践中，可以将多个指标综合起来看，以确定最终的显著变量范围，而不是仅使用一个指标来进行判断和筛选。

3.2 基于机器学习的方法

（0）准备工作

为了更能体现基于机器学习的变量筛选的效果，向cancer数据集中增加噪声特征。

#增加噪声数据

import numpy as np

rng = np.random.RandomState(33)     #设定种子数，保证生成的随机数相同

noise = rng.normal(size=(len(data),50))   #基于这个随机数产生一个50个维度的正态分布数据

noiseDf = pd.DataFrame(noise)

dataNoiseDf = pd.concat([dataDf,noiseDf],axis=1)    #与噪声数据合并

#划分样本集

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(dataNoiseDf, targetSer, random_state=33, test_size=0.40)    #划分训练集和测试集

（1）单一模型

SelectFromModel是sklearn中用于基于模型的特征选择的类，它可以选出重要性程度大于给定阈值的所有特征。

##基于单一算法

from sklearn.feature_selection import SelectFromModel

from sklearn.ensemble import RandomForestClassifier

select1 = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=0), threshold='median')    #使用中位数作为阈值，选出40个显著特征

select1.fit(X_train, y_train)

X_train_l1 = select1.transform(X_train)

print("X_train.shape:{}".format(X_train.shape))

print("X_train_l1.shape:{}".format(X_train_l1.shape))

#可视化判定结果，黑色为显著特征，白色为非显著特征

import matplotlib.pyplot as plt

mask1 = select1.get_support()

print("Effective Features:{}".format(list(mask1)))

plt.matshow(mask1.reshape(1,-1), cmap='gray_r')

plt.xlabel("Feature Index")

结果如下：

Out[20]:

X_train.shape:(341, 80)

X_train_l1.shape:(341, 40)

Effective Features:[True, True, True, True, True, True, True, True, True, True, True, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, False, True, False, True, False, False, False, False, False, False, True, True, False, True, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, False, True, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, True]

从图中可以清晰看到，只有1个原始特征没有被选择，并且大多数噪声特征都被剔除掉。

（2）迭代

RFE（recursive feature elimination，递归特征消除）是sklearn中一种基于迭代的特征选择类，它从所有特征开始构建模型，并根据模型舍弃最不重要的特征，然后使用除了被舍弃的特征之外的全部特征构建一个新模型，如此反复，直到仅剩下预设数量的特征为止。

##基于迭代

from sklearn.feature_selection import RFE

select2 = RFE(RandomForestClassifier(n_estimators=100, random_state=42), n_features_to_select=40)   #直接设定最后要保留的特征个数为40个

select2.fit(X_train, y_train)

X_train_l2 = select2.transform(X_train)

#可视化判定结果，黑色为显著特征，白色为非显著特征

mask2 = select2.get_support()

print("Effective Features:{}".format(list(mask2)))

plt.matshow(mask2.reshape(1,-1), cmap='gray_r')

plt.xlabel("Feature Index")

结果如下：

Out[22]:

Effective Features:[True, True, True, True, True, True, True, True, True, True, True, False, True, True, True, False, True, True, False, False, True, True, True, True, True, True, True, True, True, True, False, False, False, True, True, True, True, False, False, False, False, True, False, True, False, False, False, False, False, False, False, False, False, False, False, True, False, True, False, True, False, False, False, True, False, True, False, False, False, True, True, False, False, False, False, False, False, False, False, True]

从图中可以清晰看到，有4个原始特征没有被选择，并且大多数噪声特征都被剔除掉，相比上一种基于单模型的效果要差一点。

4. 参考与感谢

[1] Python机器学习基础教程

[2] Python数据分析与数据化运营

[3] sklearn.datasets.load_breast_cancer

[4] sklearn.feature_selection.SelectFromModel

[5] sklearn.feature_selection.RFE

数据准备<5>:变量筛选-实战篇的更多相关文章

  1. 数据准备<4>:变量筛选-理论篇

    在上一篇文章<数据准备<3>:数据预处理>中,我们提到降维主要包括两种方式:基于特征选择的降维和基于维度转换的降维,其中基于特征选择的降维通俗的讲就是特征筛选或者变量筛选,是指 ...

  2. Systemd 入门教程：实战篇

    Systemd 入门教程:实战篇 上一篇文章,介绍了 Systemd 的主要命令,这篇文章主要介绍如何使用 Systemd 来管理我们的服务,以及各项的含义: 一.开机启动 对于那些支持 System ...

  3. VB6基本数据库应用（五）：数据的查找与筛选

    同系列的第五篇,上一篇在:http://blog.csdn.net/jiluoxingren/article/details/9633139 数据的查找与筛选 第4篇发布到现在已经过了4天,很抱歉,学 ...

  4. Ceres Solver: 高效的非线性优化库（二）实战篇

    Ceres Solver: 高效的非线性优化库(二)实战篇 接上篇: Ceres Solver: 高效的非线性优化库(一) 如何求导 Ceres Solver提供了一种自动求导的方案,上一篇我们已经看 ...

  5. 《大数据实时计算引擎 Flink 实战与性能优化》新专栏

    基于 Flink 1.9 讲解的专栏,涉及入门.概念.原理.实战.性能调优.系统案例的讲解. 专栏介绍 扫码下面专栏二维码可以订阅该专栏 首发地址:http://www.54tianzhisheng. ...

  6. 如何编写高质量的 JS 函数（4） --函数式编程[实战篇]

    本文首发于 vivo互联网技术 微信公众号 链接:https://mp.weixin.qq.com/s/ZoXYbjuezOWgNyJKmSQmTw作者:杨昆 [编写高质量函数系列],往期精彩内容: ...

  7. 算法---FaceNet在Tf下的实战篇

    FaceNet---Tensorflow下的下的实战篇 @WP20190225 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝目录＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ 一.FaceNet算法简介 二.FaceNet配置与使 ...

  8. SAS数据挖掘实战篇【五】

    SAS数据挖掘实战篇[五] SAS--预测模型 6.1 测模型介绍 预测型(Prediction)是指由历史的和当前的数据产生的并能推测未来数据趋势的知识.这类知识可以被认为是以时 间为关键属性的关联 ...

  9. SAS数据挖掘实战篇【四】

    SAS数据挖掘实战篇[四] 今天主要是介绍一下SAS的聚类案例,希望大家都动手做一遍,很多问题只有在亲自动手的过程中才会有发现有收获有心得. 1 聚类分析介绍 1.1 基本概念 聚类就是一种寻找数据之 ...

随机推荐

  1. Django 安装 —Django学习 （一）

    Django Django 是一个python 框架, 采用MTV的模式,模型,模板,视图 注意事项 Django 版本和 python 的版本是一一对应的,安装时一定要注意相应的版本信息. 如下图: ...

  2. [转]ROS(Robot Operating System)常用环境变量介绍

    本文简单介绍ROS系统中常用的环境变量用途及设置方式.ROS系统环境中除了必须配置的环境变量以外,其他的也是十分有用,通过修改变量路径,可以设置ROS系统中log文件存放路径,单元测试结果存放路径等. ...

  3. 防范xss的正确姿势

    防范xss的正确姿势 xss攻击是web攻击中非常常见的一种攻击手段.如果你还没有听说过xss攻击,可以先了解xss的相关知识和原理,例如: XSS)" target="_blan ...

  4. java所搜引擎slor学习笔记(一)

    java搜索引擎有很多,比较熟悉的就是slor和lucene. luncene: 概念:全文检索是计算机程序通过扫描文章中的每一个词,对每一个词建立一个索引,指明该词在文章中出现的次数和位置.当用户查 ...

  5. Oracle数据库中几种常见的SCN

    控制文件中的SCN 数据文件头的SCN 数据块中的SCN 日志文件头中的SCN 事务SCN 内存中的SCN 一 控制文件中的SCN 1.1 数据库SCN 数据库SCN表示最近一次全量checkpoin ...

  6. Fiddler 4 抓包（APP HTTPS ）

    一.手机连接Fiddler 1.配置fiddler 1.安装fiddler,基本下一步下一步即可: 2.打开fiddler,点击顶部栏Tools——>Options 3.在HTTPS页签勾选“D ...

  7. 10 个优质的 Laravel 扩展推荐

    这里有 10+ 个用来搭建 Laravel 应用的包 为何会创建这个包的列表?因为我是一个「比较懒」的开发者,在脸书上是多个 Laravel 小组的成员.平日遇到最多的问题就是开发是需要用那些包.我很 ...

  8. POJ 2516 Minimum Cost(拆点+KM完备匹配)

    题目链接:http://poj.org/problem?id=2516 题目大意: 第一行是N,M,K 接下来N行:第i行有K个数字表示第i个卖场对K种商品的需求情况 接下来M行:第j行有K个数字表示 ...

  9. css 让背景图片不停旋转

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  10. 在SQL中有时候我们需要查看现在正在SQL Server执行的命令

    在SQL中有时候我们需要查看现在正在SQL Server执行的命令.在分析管理器或者Microsoft SQL Server Management Studio中,我们可以在"管理-SQL  ...