NYOJ 1058 部分和问题

部分和问题

时间限制：1000 ms  |  内存限制：65535 KB

难度：2

 

描述

给定整数a1、a2、.......an，判断是否可以从中选出若干数，使它们的和恰好为K。

 

输入

首先，n和k，n表示数的个数，k表示数的和。
接着一行n个数。
（1<=n<=20,保证不超int范围）

输出

如果和恰好可以为k，输出“YES”，并按输入顺序依次输出是由哪几个数的和组成，否则“NO”

样例输入

4 13
1 2 4 7

样例输出

YES
2 4 7

原题来自：http://acm.nyist.net/JudgeOnline/problem.php?pid=1058

分析如下：

从num[0]开始按顺序决定每个数加或者不加，在全部N个数都决定后在判断他们的和是不是和k相等。

因为状态数是2^{n+1 ，}所以复杂度是O(2ⁿ)。

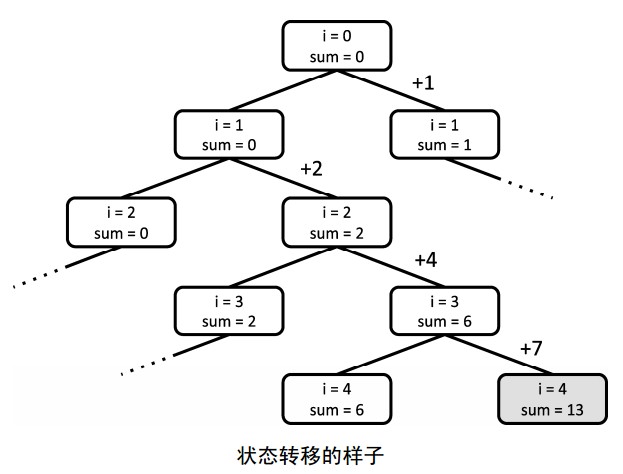
代码如下：

 #include <stdio.h>

 int n,k,pos;
 int num[];   // 输入的数据
 int TTT[];   // 哪几个数构造的数组 

 bool dfs(int i,int sum)
 {
     if(i==n)return sum==k;
     else if(sum>k)return false;
     //不+情况
     if(dfs(i+,sum))return true;
     //+的情况
     if(dfs(i+,num[i]+sum))
     {
         TTT[pos++]=num[i];
         return true;
     }
     return false;
 }

 int main()
 {
     while(~scanf("%d%d",&n,&k))
     {
         pos=;
         for(int i=;i<n;i++)
             scanf("%d",&num[i]);
         if(dfs(,))
         {
             printf("YES\n");
             for(int i=pos-;i>;i--)
                 printf("%d ",TTT[i]);
             printf("%d\n",TTT[]);
         }
         else printf("NO\n");
     }
     return ;
 }