hdu 2044 一只小蜜蜂
斐波那契数列变形,在本题中不是从1-N,而是从M-N
下标 1 2 3 4 5 6 7 8 9
值 1 1 2 3 5 8 13 21 34(每一项都是前两项的和)
小蜜蜂走蜂房
1-2 1种 12
1-3 2种 123 13
1-4 3种 124 134 1234
那么可以看成走楼梯问题
给出两个值,a,b,当前在a阶,到b阶有多少种走法。
那么,可以将a看成是第0阶,b则可以看成(b-a)
下标 0 1 2 3 4 5
值 0 1 2 3 5 8
(可能看出下标2 有点不对,但我们要根据题意,自行定义,这里先自定义好前三项,当然还可以把0下标值为1,因为本题中0<a<b<50,AC代码中就是按后者这样做的)
从第 0 阶到第1阶有1种
从第 0 阶到第2阶有2种
从第 a 阶到第b阶则有f[b-a]中
举例 从5到第7阶,你可以想象一下,在有限定条件下,那么你能有几种方法从5阶走到第7阶呢?是不是和从第 0 阶到第 2阶是一个道理呢?
看到这里,你应该知道怎么做了吧。
#include<stdio.h>
int main(void)
{
int i,n,a,b;
long long narr[55];
narr[0]=1;narr[1]=1;
for(i=2;i<51;i++)
{
narr[i]=narr[i-1]+narr[i-2];
}
scanf("%d",&n);
while(n--)
{
scanf("%d%d",&a,&b);
printf("%lld\n",narr[b-a]);
}
return 0;
}
hdu 2044 一只小蜜蜂的更多相关文章
- hdu 2044:一只小蜜蜂...(水题,斐波那契数列)
一只小蜜蜂... Time Limit: / MS (Java/Others) Memory Limit: / K (Java/Others) Total Submission(s): Accepte ...
- HDU 2044 一只小蜜蜂(递归)
一只小蜜蜂... Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Su ...
- hdu 2044 一只小蜜蜂...(简单dp)
一只小蜜蜂... Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Su ...
- HDU 2044——一只小蜜蜂...(DP)
链接:http://acm.hdu.edu.cn/showproblem.php?pid=2044 题解 //递归思想,超时 #include<iostream> using namesp ...
- HDU 2044 一只小蜜蜂... (斐波那契数列)
原题链接:http://acm.hdu.edu.cn/showproblem.php?pid=2044 题目分析:其实仔细读题就会发现其中的规律, 其中:这是一个典型的斐波那契数列. 代码如下: #i ...
- ACM HDU 2044 一只小蜜蜂
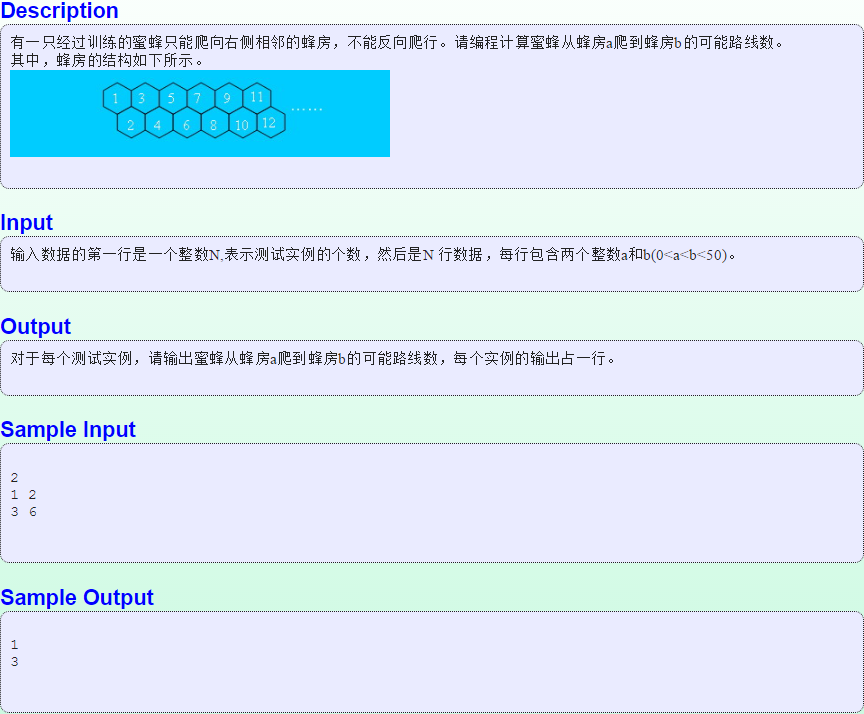
Problem Description 有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行.请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数. 其中,蜂房的结构如下所示. Input 输入数据的第一 ...
- HDU 2044 一只小蜜蜂...(递推,Fibonacci)
题意:中文题. 析:首先要想到达第 n 个蜂房,那么必须经 第 n-1 或第 n-2 个蜂房,那么从第 n-1 或第 n-2 个蜂房到达第 n 个,都各自有一条路线, 所以答案就是第 n-1 + 第 ...
- HDU - 2044 - 一只小蜜蜂...(dp)
题意: 如题 思路: 仔细观察图 1-4和3-6其实是一样的答案,那么所有的方案都可以相减,意思为全部转化为从1开始 剩下的就是观察规律,仔细观察5号,能到5号蜂房的只有3和4,3和4到5号蜂房只有一 ...
- hdoj 2044一只小蜜蜂...【斐波那契变形】
一只小蜜蜂... Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Su ...
随机推荐
- 一份高级Java招聘要求
搜了一些招聘,发现自己还有很长的路要走啊,学无止境...... 摘一个典型的招聘要求,如下: 1.5年基于java的项目开发经验,2.熟悉基于 J2EE的相关开源技术以及Spring,Struts2, ...
- Eclipse里面启用genymotion
E:/Users/zhuxuekui/AppData/Local/Android/sdk as里面的SDK目录 1.打开eclipse并从云仓库里面下载genymotion插件 注意:这里面有一个坑, ...
- Vs2012 中使用itoa
自己在写程序的时候经常用到保存大量的图片,从而对其编号,所以要把整型转换成字符型. 通常自己定义string,而字符使用char[],把整形转换成char类型,然后和string类型相加,但是在VS2 ...
- Java学习笔记(二一)——Java 泛型
[前面的话] 最近脸好干,掉皮,需要买点化妆品了. Java泛型好好学习一下. [定义] 一.泛型的定义主要有以下两种: 在程序编码中一些包含类型参数的类型,也就是说泛型的参数只可以代表类,不能代表个 ...
- 3、面向对象以及winform的简单运用(类的初步认识)
什么是类? “类”是面向对象编程的基本单元,一个类一般包含两种成员:字段和方法——即变量和函数. 例: //字段或变量的定义 public int age; //方法或函数的定义 public int ...
- 最新 Sublime Text3 激活码 (Build 3114 有效)
今天打开Sublime Text 3 有更新,更新了一下然后之前的激活就失效了.无奈只好重新搜索可用的激活码.不过幸运的是我搜索到了很多可用的激活码,不敢独专. // Sublime Text 3 L ...
- 笔记:js的replace函数
replace函数 js的replace函数与c#的有一个不同,js的只替换第一个字符 例如,var a=',1,2' var b=a.replace(',','') 结果b='1,2'(ps:这是一 ...
- 使用Struts2和jQuery EasyUI实现简单CRUD系统(转载汇总)
使用Struts2和jQuery EasyUI实现简单CRUD系统(一)——从零开始,ajax与Servlet的交互 使用Struts2和jQuery EasyUI实现简单CRUD系统(二)——aja ...
- C基础--结构体
C语言,结构体语法: 1.定义结构体类型: struct 结构体名称 { 成员类型 成员名称1; 成员类型 成员名称2; ... }; 例:struct Date { int year ; int m ...
- offsetLeft, offsetTop以及postion().left , postion().top有神马区别
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...
