JavaScript 数据结构与算法之美 - 你可能真的不懂递归

1. 前言

1. 算法为王。
2. 排序算法博大精深，前辈们用了数年甚至一辈子的心血研究出来的算法，更值得我们学习与推敲。

因为之后要讲有内容和算法，其代码的实现都要用到递归，所以，搞懂递归非常重要。

2. 定义

• 方法或函数调用自身的方式称为递归调用，调用称为递，返回称为归。
  
  简单来说就是：自己调用自己。

现实例子：周末你带着女朋友去电影院看电影，女朋友问你，咱们现在坐在第几排啊 ？电影院里面太黑了，看不清，没法数，现在你怎么办 ？

于是你就问前面一排的人他是第几排，你想只要在他的数字上加一，就知道自己在哪一排了。

但是，前面的人也看不清啊，所以他也问他前面的人。

就这样一排一排往前问，直到问到第一排的人，说我在第一排，然后再这样一排一排再把数字传回来。

直到你前面的人告诉你他在哪一排，于是你就知道答案了。

基本上，所有的递归问题都可以用递推公式来表示，比如:

f(n) = f(n-1) + 1;
// 其中，f(1) = 1

f(n) 表示你想知道自己在哪一排，f(n-1) 表示前面一排所在的排数，f(1) = 1 表示第一排的人知道自己在第一排。

有了这个递推公式，我们就可以很轻松地将它改为递归代码，如下：

function f(n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

3. 为什么使用递归 ？递归的优缺点 ？

• 优点：代码的表达力很强，写起来简洁。
• 缺点：空间复杂度高、有堆栈溢出风险、存在重复计算、过多的函数调用会耗时较多等问题。

4. 什么样的问题可以用递归解决呢 ？

一个问题只要同时满足以下 3 个条件，就可以用递归来解决。

• 问题的解可以分解为几个子问题的解。何为子问题 ？就是数据规模更小的问题。
  
  比如，前面讲的电影院的例子，你要知道，自己在哪一排的问题，可以分解为前一排的人在哪一排这样一个子问题。
• 问题与子问题，除了数据规模不同，求解思路完全一样
  
  比如电影院那个例子，你求解自己在哪一排的思路，和前面一排人求解自己在哪一排的思路，是一模一样的。
• 存在递归终止条件
  
  比如电影院的例子，第一排的人不需要再继续询问任何人，就知道自己在哪一排，也就是 f(1) = 1，这就是递归的终止条件。

5. 递归常见问题及解决方案

• 警惕堆栈溢出：可以声明一个全局变量来控制递归的深度，从而避免堆栈溢出。
• 警惕重复计算：通过某种数据结构来保存已经求解过的值，从而避免重复计算。

6. 如何实现递归 ？

1. 递归代码编写

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

2. 递归代码理解

对于递归代码，若试图想清楚整个递和归的过程，实际上是进入了一个思维误区。

那该如何理解递归代码呢 ？

• 如果一个问题 A 可以分解为若干个子问题 B、C、D，你可以假设子问题 B、C、D 已经解决。
• 而且，你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可，不需要一层层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。
• 屏蔽掉递归细节，这样子理解起来就简单多了。

因此，理解递归代码，就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

7. 例子

1. 一个阶乘的例子：

function fact(num) {
  if (num <= 1) {
    return 1;
  } else {
    return num * fact(num - 1);
    }
}
fact(3) // 结果为 6

以下代码可导致出错：

var anotherFact = fact;
fact = null;
alert(antherFact(4)); //出错

由于 fact 已经不是函数了，所以出错。

使用 arguments.callee

arguments.callee 是一个指向正在执行的函数的指针，arguments.callee 返回正在被执行的对现象。

新的函数为：

function fact(num){
    if (num <= 1){
        return 1;
    }else{
        return num * arguments.callee(num - 1); //此处更改了。
    }
}
var anotherFact = fact;
fact = null;
alert(antherFact(4)); // 结果为 24

2. 再看一个多叉树的例子

先看图

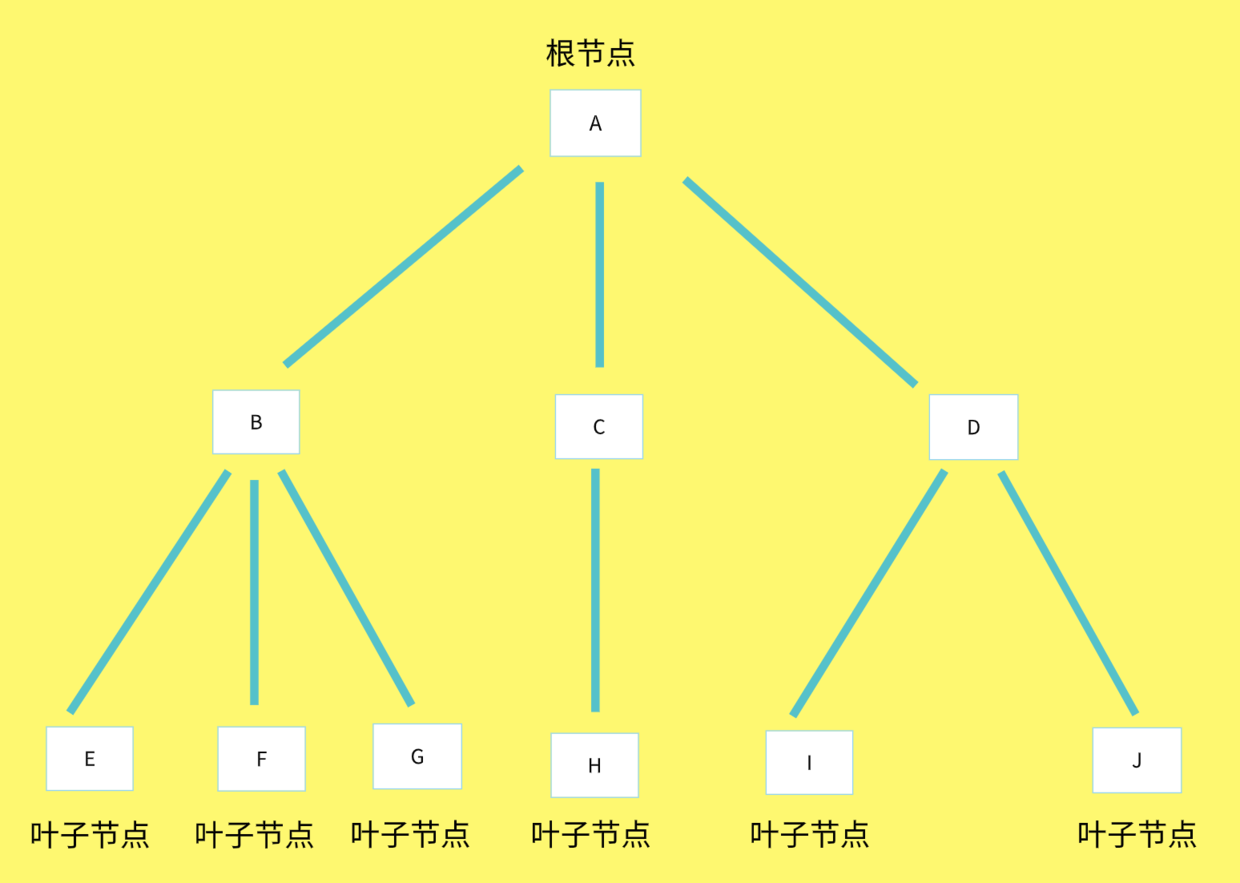
叶子结点：就是深度为 0 的结点，也就是没有孩子结点的结点，简单的说就是一个二叉树任意一个分支上的终端节点。

数据结构格式，参考如下代码：

const json = {
  name: 'A',
  children: [
    {
      name: 'B',
      children: [
        {
          name: 'E',
        },
        {
          name: 'F',
        },
        {
          name: 'G',
        }
      ]
    },
    {
      name: 'C',
      children: [
        {
          name: 'H'
        }
      ]
    },
    {
      name: 'D',
      children: [
        {
          name: 'I',
        },
        {
          name: 'J',
        }
      ]
    }
  ]
}

我们如何获取根节点的所有叶子节点个数呢 ？

递归代码如下：

/**
 * 获取根节点的所有 叶子节点 个数
 * @param {Object} json Object 对象
 */
function getLeafCountTree(json) {
  if(!json.children){
      return 1;
  } else {
      let leafCount = 0;
      for(let i = 0 ; i < json.children.length ; i++){
          // leafCount = leafCount + getLeafCountTree(json.children[i]);
          leafCount = leafCount + arguments.callee(json.children[i]);
      }
      return leafCount;
  }
}

递归遍历是比较常用的方法，比如：省市区遍历成树、多叉树、阶乘等。

8. 最后

如果觉得本文还不错，记得给个 star ， 你的 star 是我持续更新的动力！。

笔者 GitHub。

参考文章：

递归：如何用三行代码找到“最终推荐人”？