数据结构与算法---查找算法(Search Algorithm)

查找算法介绍

在java中，我们常用的查找有四种:

1. 顺序(线性)查找
2. 二分查找/折半查找
3. 插值查找
4. 斐波那契查找

1)线性查找算法

示例：

有一个数列： {1,8, 10, 89, 1000, 1234} ，判断数列中是否包含此名称【顺序查找】 要求: 如果找到了，就提示找到，并给出下标值。

思路：将数列遍历匹配，就是用for循坏遍历，if匹配数据，找到下标值输出。

 public class SeqSearch {

     public static void main(String[] args) {
         int arr[] = { 1, 9, 11, -1, 34, 89 };// 没有顺序的数组
         int index = seqSearch(arr, -11);
         if(index == -1) {
             System.out.println("没有找到到");
         } else {
             System.out.println("找到，下标为=" + index);
         }
     }

     /**
      * 这里我们实现的线性查找是找到一个满足条件的值，就返回
      * @param arr
      * @param value
      * @return
      */
     public static int seqSearch(int[] arr, int value) {
         // 线性查找是逐一比对，发现有相同值，就返回下标
         for (int i = 0; i < arr.length; i++) {
             if(arr[i] == value) {
                 return i;
             }
         }
         return -1;
     }

 }

代码

2)二分查找算法

示例：

请对一个有序数组进行二分查找 {1,8, 10, 89, 1000, 1234} ，输入一个数看看该数组是否存在此数，并且求出下标，如果没有就提示"没有这个数"。

思路：

 public static void main(String[] args) {
         //int arr[] = { 1, 8, 10, 89,1000,1000, 1234 };
         int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12, 13,14,15,16,17,18,19,20 };

         //
         int resIndex = binarySearch(arr, 0, arr.length - 1, 1000);
         System.out.println("resIndex=" + resIndex);

         //List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1);
         //System.out.println("resIndexList=" + resIndexList);
     }

     // 二分查找算法
     /**
      *
      * @param arr
      *            数组
      * @param left
      *            左边的索引
      * @param right
      *            右边的索引
      * @param findVal
      *            要查找的值
      * @return 如果找到就返回下标，如果没有找到，就返回 -1
      */
     public static int binarySearch(int[] arr, int left, int right, int findVal) {

         // 当 left > right 时，说明递归整个数组，但是没有找到
         if (left > right) {
             return -1;
         }
         int mid = (left + right) / 2;
         int midVal = arr[mid];

         if (findVal > midVal) { // 向 右递归
             return binarySearch(arr, mid + 1, right, findVal);
         } else if (findVal < midVal) { // 向左递归
             return binarySearch(arr, left, mid - 1, findVal);
         } else {

             return mid;
         }

     }

代码

拓展：

当一个有序数组中，有多个相同的数值时，如何将所有的数值都查找到，比如这里的 1000，{1,8, 10, 89, 1000, 1000，1234}

要查找出该数列中1000的下标，又怎么找出呢？

思路：

1. 在找到mid 索引值，不要马上返回
2. 向mid 索引值的左边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
3. 向mid 索引值的右边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
4. 将Arraylist返回

 public static void main(String[] args) {
         //int arr[] = { 1, 8, 10, 89,1000,1000, 1234 };
         int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12, 13,14,15,16,17,18,19,20 };

         //
 //        int resIndex = binarySearch(arr, 0, arr.length - 1, 1000);
 //        System.out.println("resIndex=" + resIndex);

         List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1);
         System.out.println("resIndexList=" + resIndexList);
     }

     // 二分查找算法
     /**
      *
      * @param arr
      *            数组
      * @param left
      *            左边的索引
      * @param right
      *            右边的索引
      * @param findVal
      *            要查找的值
      * @return 如果找到就返回下标，如果没有找到，就返回 -1
      */
     public static int binarySearch(int[] arr, int left, int right, int findVal) {

         // 当 left > right 时，说明递归整个数组，但是没有找到
         if (left > right) {
             return -1;
         }
         int mid = (left + right) / 2;
         int midVal = arr[mid];

         if (findVal > midVal) { // 向 右递归
             return binarySearch(arr, mid + 1, right, findVal);
         } else if (findVal < midVal) { // 向左递归
             return binarySearch(arr, left, mid - 1, findVal);
         } else {

             return mid;
         }

     }

     /*
      * {1,8, 10, 89, 1000, 1000，1234} 当一个有序数组中，
      * 有多个相同的数值时，如何将所有的数值都查找到，比如这里的 1000
      *
      * 思路分析
      * 1. 在找到mid 索引值，不要马上返回
      * 2. 向mid 索引值的左边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
      * 3. 向mid 索引值的右边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
      * 4. 将Arraylist返回
      */

     public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {

         System.out.println("hello~");
         // 当 left > right 时，说明递归整个数组，但是没有找到
         if (left > right) {
             return new ArrayList<Integer>();
         }
         int mid = (left + right) / 2;
         int midVal = arr[mid];

         if (findVal > midVal) { // 向 右递归
             return binarySearch2(arr, mid + 1, right, findVal);
         } else if (findVal < midVal) { // 向左递归
             return binarySearch2(arr, left, mid - 1, findVal);
         } else {
 //             * 思路分析
 //             * 1. 在找到mid 索引值，不要马上返回
 //             * 2. 向mid 索引值的左边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
 //             * 3. 向mid 索引值的右边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
 //             * 4. 将Arraylist返回

             List<Integer> resIndexlist = new ArrayList<Integer>();
             //向mid 索引值的左边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
             int temp = mid - 1;
             while(true) {
                 if (temp < 0 || arr[temp] != findVal) {//退出
                     break;
                 }
                 //否则，就temp 放入到 resIndexlist
                 resIndexlist.add(temp);
                 temp -= 1; //temp左移
             }
             resIndexlist.add(mid);  //

             //向mid 索引值的右边扫描，将所有满足 1000， 的元素的下标，加入到集合ArrayList
             temp = mid + 1;
             while(true) {
                 if (temp > arr.length - 1 || arr[temp] != findVal) {//退出
                     break;
                 }
                 //否则，就temp 放入到 resIndexlist
                 resIndexlist.add(temp);
                 temp += 1; //temp右移
             }

             return resIndexlist;
         }

     }

代码

3)插值查找

插值查找原理介绍:

1.插值查找算法类似于二分查找，不同的是插值查找每次从自适应mid处开始查找。

2.将折半查找中的求mid 索引的公式 , low 表示左边索引left, high表示右边索引right. key 就是前面我们讲的 findVal

3.int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low])  ;/*插值索引*/

对应前面的代码公式：

int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])

举例说明插值查找算法 1-100 的数组

 public static void main(String[] args) {

 //        int [] arr = new int[100];
 //        for(int i = 0; i < 100; i++) {
 //            arr[i] = i + 1;
 //        }

         int arr[] = { 1, 8, 10, 89,1000,1000, 1234 };

         int index = insertValueSearch(arr, 0, arr.length - 1, 1234);
         //int index = binarySearch(arr, 0, arr.length, 1);
         System.out.println("index = " + index);

         //System.out.println(Arrays.toString(arr));
     }

     public static int binarySearch(int[] arr, int left, int right, int findVal) {
         System.out.println("二分查找被调用~");
         // 当 left > right 时，说明递归整个数组，但是没有找到
         if (left > right) {
             return -1;
         }
         int mid = (left + right) / 2;
         int midVal = arr[mid];

         if (findVal > midVal) { // 向 右递归
             return binarySearch(arr, mid + 1, right, findVal);
         } else if (findVal < midVal) { // 向左递归
             return binarySearch(arr, left, mid - 1, findVal);
         } else {

             return mid;
         }

     }

     //编写插值查找算法
     //说明：插值查找算法，也要求数组是有序的
     /**
      *
      * @param arr 数组
      * @param left 左边索引
      * @param right 右边索引
      * @param findVal 查找值
      * @return 如果找到，就返回对应的下标，如果没有找到，返回-1
      */
     public static int insertValueSearch(int[] arr, int left, int right, int findVal) { 

         System.out.println("插值查找次数~~");

         //注意：findVal < arr[0]  和  findVal > arr[arr.length - 1] 必须需要
         //否则我们得到的 mid 可能越界
         if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
             return -1;
         }

         // 求出mid, 自适应
         int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
         int midVal = arr[mid];
         if (findVal > midVal) { // 说明应该向右边递归
             return insertValueSearch(arr, mid + 1, right, findVal);
         } else if (findVal < midVal) { // 说明向左递归查找
             return insertValueSearch(arr, left, mid - 1, findVal);
         } else {
             return mid;
         }

     }

代码

插值查找注意事项：

1.对于数据量较大，关键字分布比较均匀的查找表来说，采用插值查找, 速度较快.

2.关键字分布不均匀的情况下，该方法不一定比折半查找要好

4)斐波那契(黄金分割法)查找算法

斐波那契(黄金分割法)查找基本介绍:

1.黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽，因此称为黄金分割，也称为中外比。这是一个神奇的数字，会带来意向不大的效果。

2.斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55 } 发现斐波那契数列的两个相邻数 的比例，无限接近 黄金分割值0.618

斐波那契(黄金分割法)原理:

斐波那契查找原理与前两种相似，仅仅改变了中间结点（mid）的位置，mid不再是中间或插值得到，而是位于黄金分割点附近，即mid=low+F(k-1)-1

F代表斐波那契数列），如下图所示

对F(k-1)-1的理解：

1.由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质，可以得到 （F[k]-1）=（F[k-1]-1）+（F[k-2]-1）+1 。该式说明：只要顺序表的长度为F[k]-1，则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段，即如上图所示。从而中间位置为mid=low+F(k-1)-1

2.类似的，每一子段也可以用相同的方式分割

3.但顺序表长度n不一定刚好等于F[k]-1，所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或等于n即可，由以下代码得到,顺序表长度增加后，新增的位置（从n+1到F[k]-1位置），都赋为n位置的值即可。

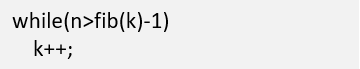
斐波那契查找应用案例：

请对一个有序数组进行斐波那契查找 {1,8, 10, 89, 1000, 1234} ，输入一个数看看该数组是否存在此数，并且求出下标，如果没有就提示"没有这个数"。

 public static int maxSize = 20;
     public static void main(String[] args) {
         int [] arr = {1,8, 10, 89, 1000, 1234};

         System.out.println("index=" + fibSearch(arr, 189));//

     }

     //因为后面我们mid=low+F(k-1)-1，需要使用到斐波那契数列，因此我们需要先获取到一个斐波那契数列
     //非递归方法得到一个斐波那契数列
     public static int[] fib() {
         int[] f = new int[maxSize];
         f[0] = 1;
         f[1] = 1;
         for (int i = 2; i < maxSize; i++) {
             f[i] = f[i - 1] + f[i - 2];
         }
         return f;
     }

     //编写斐波那契查找算法
     //使用非递归的方式编写算法
     /**
      *
      * @param a  数组
      * @param key 我们需要查找的关键码(值)
      * @return 返回对应的下标，如果没有-1
      */
     public static int fibSearch(int[] a, int key) {
         int low = 0;
         int high = a.length - 1;
         int k = 0; //表示斐波那契分割数值的下标
         int mid = 0; //存放mid值
         int f[] = fib(); //获取到斐波那契数列
         //获取到斐波那契分割数值的下标
         while(high > f[k] - 1) {
             k++;
         }
         //因为 f[k] 值 可能大于 a 的 长度，因此我们需要使用Arrays类，构造一个新的数组，并指向temp[]
         //不足的部分会使用0填充
         int[] temp = Arrays.copyOf(a, f[k]);
         //实际上需求使用a数组最后的数填充 temp
         //举例:
         //temp = {1,8, 10, 89, 1000, 1234, 0, 0}  => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
         for(int i = high + 1; i < temp.length; i++) {
             temp[i] = a[high];
         }

         // 使用while来循环处理，找到我们的数 key
         while (low <= high) { // 只要这个条件满足，就可以找
             mid = low + f[k - 1] - 1;
             if(key < temp[mid]) { //我们应该继续向数组的前面查找(左边)
                 high = mid - 1;
                 //为甚是 k--
                 //说明
                 //1. 全部元素 = 前面的元素 + 后边元素
                 //2. f[k] = f[k-1] + f[k-2]
                 //因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
                 //即 在 f[k-1] 的前面继续查找 k--
                 //即下次循环 mid = f[k-1-1]-1
                 k--;
             } else if ( key > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
                 low = mid + 1;
                 //为什么是k -=2
                 //说明
                 //1. 全部元素 = 前面的元素 + 后边元素
                 //2. f[k] = f[k-1] + f[k-2]
                 //3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
                 //4. 即在f[k-2] 的前面进行查找 k -=2
                 //5. 即下次循环 mid = f[k - 1 - 2] - 1
                 k -= 2;
             } else { //找到
                 //需要确定，返回的是哪个下标
                 if(mid <= high) {
                     return mid;
                 } else {
                     return high;
                 }
             }
         }
         return -1;
     }

代码