AcWing 166. 数独

题目地址 https://www.acwing.com/problem/content/description/168/

题目描述

数独是一种传统益智游戏，你需要把一个9 × 9的数独补充完整，使得图中每行、每列、每个3 × 3的九宫格内数字1~9均恰好出现一次。

请编写一个程序填写数独。

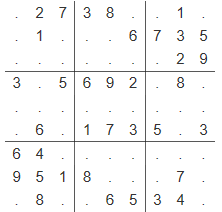
输入格式
输入包含多组测试用例。

每个测试用例占一行，包含81个字符，代表数独的81个格内数据（顺序总体由上到下，同行由左到右）。

每个字符都是一个数字（1-9）或一个”.”（表示尚未填充）。

您可以假设输入中的每个谜题都只有一个解决方案。

文件结尾处为包含单词“end”的单行，表示输入结束。

输出格式
每个测试用例，输出一行数据，代表填充完全后的数独。

样例

输入样例：
...............293.5692............6.1745................
........8.4............5.1.................................7.4........
end
输出样例：

法1
时间卡的比较紧,搜索上做了许多优化

1 进行可填写数据的筛选.由于数独本身的性质，1~9同一数字不能在同一行 同一列 同一九宫格出现两次以上。
我开始计划是开一个 9*9的数组记录每个格子可能出现的数字.每次确认填写一个数字 就更新同行同列同九宫格里的记录
但是这样的话，每次填写一个数字及需要更新 一行9个 一列9个 和九宫格九格的数据。共27个数据。
YXC大佬的代码 使用的 行记录一个 列记录一个 九宫格记录一个 这样只需要更新三个数据即可

2 优化填写格子的策略，每个格子可填写的数据比较少的优先选取。 这也是剪枝的一种.
代码见

 //找到可选方案数最少的空格
    int minv = ;
    int x, y;
    for(int i = ;i < N;i++)
        for(int j = ;j < N;j++)
            if (str[i*+j] == '.') {
                int t = ones[get(i, j)];
                if (t < minv) {
                    minv = t;
                    x = i, y = j;
                }
            }

3 一些其他小技巧，使用位来记录该空格可填写那些数字
000000001 表示可填写1
000000010 表示可填写2
000000100 表示可填写3
000000101 表示可填写1和3
......
x = 000000111 表示可填写1 2 3。 如果我们当前选择填写2 那么只要 x - (1<<(2-1))就可以把填写2的表示去除了
代码里不是2-1 而是 可填写的数字的字母的实际值与 ‘1’的差值

4 判断是否是统一九宫格 采用 x/3==i/3 y/3 == j/3

还有其他一些小技巧 欢迎一起讨论

 #include <iostream>
 #include <algorithm>
 #include <set>

 using namespace std;

 const int N = ;

 int row[N], col[N],cell[][];

 char str[];

 int ones[ << N],map[<<N];

 inline int lowbit(int x) {
     return x & -x;
 }

 void init()
 {
     for (int i = ; i < N; i++) row[i] = col[i] = ( << N) - ;
     for (int i = ; i < ; i++)
         for (int j = ; j < ; j++)
             cell[i][j] = ( << N) - ;
 }

 inline int get(int x, int y)
 {
     return row[x] & col[y] & cell[x / ][y / ];

 }

 bool dfs(int cnt)
 {
     if (!cnt) return true;

     //找到可选方案数最少的空格
     int minv = ;
     int x, y;
     for(int i = ;i < N;i++)
         for(int j = ;j < N;j++)
             if (str[i*+j] == '.') {
                 int t = ones[get(i, j)];
                 if (t < minv) {
                     minv = t;
                     x = i, y = j;
                 }
             }

     for (int i = get(x, y); i; i -= lowbit(i)) {
         int t = map[lowbit(i)];

         //修改状态
         row[x] -=  << t;
         col[y] -=  << t;
         cell[x / ][y / ] -=  << t;
         str[x *  + y] = '' + t;
         if (dfs(cnt - )) return true;

         //回复现场
         row[x] +=  << t;
         col[y] +=  << t;
         cell[x / ][y / ] +=  << t;
         str[x *  + y] = '.';
     }

     return false;
 }

 int main()
 {
     for (int i = ; i < N; i++) map[ << i] = i;
     for (int i = ; i <  << N; i++) {
         int s = ;
         for(int j = i; j;j -= lowbit(j)) s++;
         ones[i] = s; //i的二进制表示中有s个1
     }

     while (cin >> str, str[] != 'e') {
         init();
         int cnt = ;
         for(int i =,k = ;i < N;i++)
             for(int j = ; j < N;j++,k++)
                 if (str[k] != '.') {
                     int t = str[k] - '';
                     row[i] -=  << t;
                     col[j] -=  << t;
                     cell[i / ][j / ] -=  << t;
                 }
                 else {
                     cnt++;
                 }

         dfs(cnt);
         cout << str << endl;
     }

     return ;

 }

 作者：defddr
 链接：https://www.acwing.com/solution/AcWing/content/2294/
 来源：AcWing
 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 // 11111111.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
 //

 #include <iostream>
 #include <map>
 #include <vector>
 #include <string>
 #include <stdio.h>

 using namespace std;

 /*
 .2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.
 ......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
 end
 */

 const int N = ;

 int map1[ << N];
 int Xarr[N];
 int Yarr[N];
 int SameXYArr[N / ][N / ];

 int ones[ << N], map[ << N];

 char str[];

 void Init()
 {
     for (int i = ; i < N; i++) {
         Xarr[i] = ( << N) - ;
         Yarr[i] = ( << N) - ;
         map1[ << i] = i;
     }

     for (int i = ; i < N / ; i++) {
         for (int j = ; j < N / ; j++) {
             SameXYArr[i][j] = ( << N) - ;
         }
     }
 }

 inline int lowbit(int x) {
     return x & -x;
 }

 inline int get(int x, int y)
 {
          return Xarr[x] & Yarr[y] & SameXYArr[x / ][y / ];
 }

 bool Dfs(int count, char str[])
 {
     if (!count) return true;

     int minv = ;
     int minx = -; int miny = -;

     for (int x = ; x < ; x++) {
         for (int y = ; y < ; y++)
         {
             if (str[x *  + y] == '.') {
                 int t = ones[get(x,y)];

                 if (t < minv) {
                     minv = t;
                     minx = x;
                     miny = y;
                 }
             }
         }
     }

     if ( == minv)
         return false;

     int tryNums = get(minx, miny);

     while (tryNums != ) {
         int trynum = map1[lowbit(tryNums)];

         Xarr[minx] -=  << trynum;
         Yarr[miny] -=  << trynum;
         SameXYArr[minx / ][miny / ] -=  << trynum;
         str[minx *  + miny] = '' + trynum;

         if (Dfs(count - , str))  return true;

         //回复现场
         Xarr[minx] +=  << trynum;
         Yarr[miny] +=  << trynum;
         SameXYArr[minx / ][miny / ] +=  << trynum;
         str[minx *  + miny] = '.';

         tryNums -= lowbit(tryNums);
     }

     return false;
 }

 void Do(char str[])
 {
     Init();
     int count = ;
     for (int i = ; i < ; i++) {
         for (int j = ; j < ; j++) {
             if (str[i *  + j] != '.') {
                 int idx =  << (str[i *  + j] - '');
                 Xarr[i] -= idx;
                 Yarr[j] -= idx;
                 SameXYArr[i / ][j / ] -= idx;
             }
             else {
                 count++;
             }
         }
     }

     Dfs(count, str);
     cout << str << endl;

     return;
 }

 int main()
 {
     ios::sync_with_stdio(false);

     for (int i = ; i < N; i++) map1[ << i] = i;
          for (int i = ; i <  << N; i++) {
                  int s = ;
                  for (int j = i; j; j -= lowbit(j)) s++;
                  ones[i] = s; //i的二进制表示中有s个1

     }

         while (cin >> str, str[] != 'e') {
             //s = ".2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.";

             Do(str);
         }

 }