最远 Manhattan 距离

最远 Manhattan 距离

处理问题

K维空间下的n个点，求两点最远曼哈顿距离

思路

以二维为例介绍算法思想，即可类推到k维。对于P，Q两点，曼哈顿距离|P_x-Q_x|+|P_y-Q_y|可看作(±P_x±P_y)-(±Q_x±Q_y)，不难发现P_x应该与Q_x的符号相同，P_y与Q_y符号相同，因此共四种情况。这样写的好处是，每个点可以表示成相同的形式（±P_x±P_y）。而曼哈顿距离一定是四种情况中值最大的那种，所以要求两点最远曼哈顿距离，可以枚举所有的取符号情况，对于每种情况，维护出上述表示下n个点的最大值与最小值，求出差值。则最远的曼哈顿距离一定是所有情况中的最大差值。

代码描述

ll max_Manhattan(ll p[][10],int n,int k)
{
	ll ans=0;
	for (int s=0;s<(1<<k);++s)
	{
		ll mx=-1e18,mn=1e18;
		for (int i=0;i<n;++i)
		{
			ll tmp=0;
			for (int j=0;j<k;++j)
				tmp+=(s&(1<<j))?p[i][j]:-p[i][j];
			mx=max(mx,tmp),mn=min(mn,tmp);
		}
		ans=max(ans,mx-mn);
	}
	return ans;
}

应用

一般题目可能不会太直白的要求最远曼哈顿距离，以今年多校的一道题为例，可以HDU上找到J.CSGO.

题目大意：

给n个主武器，m个副武器。每个武器有1个s属性和k个x属性。要求选取主副两把武器，使得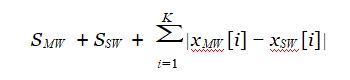最大。

思路：

现在再来看这道题，可以发现其形式很像求K维下最远曼哈顿距离。前面多的两项可以看作第k+1维，为了保证它们的形式是两项相加，将其中一个武器集合的s属性都置为负即可。然后就做一次k维下n个点和m个点之间取两点的最远曼哈顿距离。要注意，选取的点必须分属不同集合。因此我的处理方式是，每种取符号情况下，分别维护两个武器集合的最值，求差值。（也有更巧妙的处理方法，如处理两种武器的s值，最后再修正答案，这里不赘述，可以看一下该题相关博客题解）

代码：

#include<bits/stdc++.h>
#define dd(x) cout<<#x<<" = "<<x<<" "
#define de(x) cout<<#x<<" = "<<x<<"\n"
#define sz(x) int(x.size())
#define All(x) x.begin(),x.end()
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> P;
typedef priority_queue<int> BQ;
typedef priority_queue<int,vector<int>,greater<int> > SQ;
const int maxn=1e5+10,mod=1e9+7,INF=0x3f3f3f3f;
int a[maxn][10],b[maxn][10];
void cal(int p[][10],int n,int k,int sta,ll& mx,ll& mn)
{
	mx=-1e18,mn=1e18;
	for (int i=0;i<n;++i)
	{
		ll tmp=0;
		for (int j=0;j<k;++j)
		{
			if (sta&(1<<j))
				tmp+=p[i][j];
			else
				tmp-=p[i][j];
		}
		mx=max(mx,tmp),mn=min(mn,tmp);
	}
}
ll max_Manhattan(int n,int m,int k)
{
	ll ans=0,amax,amin,bmax,bmin;
	for (int sta=0;sta<(1<<k);++sta)
	{
		cal(a,n,k,sta,amax,amin);
		cal(b,m,k,sta,bmax,bmin);
		ans=max(ans,max(amax-bmin,bmax-amin));
	}
	return ans;
}
int main()
{
	int  T;
	cin>>T;
	while (T--)
	{
		int n,m,k;
		scanf("%d%d%d",&n,&m,&k);
		for (int i=0;i<n;++i)
			for (int j=0;j<=k;++j)
				scanf("%d",&a[i][j]);
		for (int i=0;i<m;++i)
		{
			for (int j=0;j<=k;++j)
				scanf("%d",&b[i][j]);
			b[i][0]*=-1;
		}
		printf("%lld\n",max_Manhattan(n,m,k+1));
	}
	return 0;
}

再附上一道CF上的题G. Multidimensional Queries

题目大意：给Ｋ维空间下的ｎ个点，编号１－ｎ。有两种操作，１重置某个编号的点的坐标，２询问某个编号区间内最远两点的曼哈顿距离。

思路：直白的求最远曼哈顿距离，不过是带有修改操作和区间询问，因此需要线段树来维护每个取符号情况下的区间最值。思想没有变化，也不需要什么技巧，不赘述。

代码：

#include<bits/stdc++.h>
#define dd(x) cout<<#x<<" = "<<x<<" "
#define de(x) cout<<#x<<" = "<<x<<endl
#define fi first
#define se second
#define mp make_pair
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
typedef vector<int> V;
typedef map<int,int> M;
typedef queue<int> Q;
typedef priority_queue<int> BQ;
typedef priority_queue<int,vector<int>,greater<int> > SQ;
const int maxn=2e5+10,INF=0x3f3f3f3f;
int a[maxn][6],mx[maxn<<2][33],mn[maxn<<2][33];
int n,k;
inline void push_up(int id)
{
	for (int s=0;s<(1<<k);++s)
		mx[id][s]=max(mx[id<<1][s],mx[id<<1|1][s]),
		mn[id][s]=min(mn[id<<1][s],mn[id<<1|1][s]);
}
void cal(int p,int id)
{
	for (int s=0;s<(1<<k);++s)
	{
		int tmp=0;
		for (int i=0;i<k;++i)
			tmp+=(s&(1<<i))?a[p][i]:-a[p][i];
		mx[id][s]=mn[id][s]=tmp;
	}
}
void build(int l,int r,int id)
{
	if (l==r)
	{
		cal(l,id);
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,id<<1);
	build(mid+1,r,id<<1|1);
	push_up(id);
}
void upd(int p,int l,int r,int id)
{
	if (l==r)
	{
		cal(p,id);
		return;
	}
	int mid=(l+r)>>1;
	if (p<=mid)
		upd(p,l,mid,id<<1);
	else
		upd(p,mid+1,r,id<<1|1);
	push_up(id);
}
void qry(int L,int R,int& Max,int& Min,int l,int r,int id,int s)
{
	if (L<=l&&r<=R)
	{
		Max=max(Max,mx[id][s]),Min=min(Min,mn[id][s]);
		return;
	}
	int mid=(l+r)>>1;
	if (R>mid)
		qry(L,R,Max,Min,mid+1,r,id<<1|1,s);
	if (L<=mid)
		qry(L,R,Max,Min,l,mid,id<<1,s);
}
int query(int L,int R)
{
	int ans=0;
	for (int s=0;s<(1<<k);++s)
	{
		int Max=-INF,Min=INF;
		qry(L,R,Max,Min,1,n,1,s);
		ans=max(ans,Max-Min);
	}
	return ans;
}
int main()
{
	cin>>n>>k;
	for (int i=1;i<=n;++i)
		for (int j=0;j<k;++j)
			scanf("%d",&a[i][j]);
	build(1,n,1);
	int q;
	cin>>q;
	while (q--)
	{
		int op;
		scanf("%d",&op);
		if (op==1)
		{
			int id;
			scanf("%d",&id);
			for (int i=0;i<k;++i)
				scanf("%d",&a[id][i]);
			upd(id,1,n,1);
		}
		else
		{
			int l,r;
			scanf("%d%d",&l,&r);
			printf("%d\n",query(l,r));
		}
	}
	return 0;
}