FZU - 2295 Human life （最大权闭合子图）

题目链接

FZU - 2295 Human life

题目分析

题意：你在玩一个游戏，在其中你可以通过学习一些技能，但是学习某些技能之前，可能还要学习一些其他的技能，并且学习任何技能都有一定的花费；

而我们可以通过掌握某些工作以获取报酬，为了掌握这一工作，我们必须学会特定的技能。

不过有些工作彼此之间是冲突的，简单来说：如果你掌握了工作A，那么将无法掌握工作B

思路：

由于技能之间也存在依赖关系，但实际上如果要获取某一工作的报酬，那么必须选择这个工作的前置技能以及前置技能的前置技能，

那么显然，这些形成依赖关系的技能都是这一工作的前置技能，所以我们的问题就是求最大权闭合子图了。

我们在工作和其所有的前置技能之间建一条容量为inf的边，然后由所有的技能向汇点建一条容量为这一技能学习消耗的边，

再由源点向每个工作建一条容量为这一工作报酬的边。

这个地方还加上了一个条件，有些工作无法同时获取，不过这个地方产生冲突最大对数为5个，那么我们枚举所有的情况就好了，

一共2^5 = 32种，根据每种状态来决定可选取的工作，并构建这一顶点及其相关的边

然后根据：最大闭合子图的权值 = 所有权值为正的结点的权值之和 - 最小割（最大流）求出答案

顺便吐糟一下这个题，首先这个OJ的C++环境不是C11标准，也就是说不支持大括号给结构体变量赋值，比如这样：

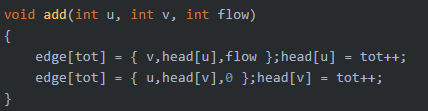
我这个语法写了近一年了，从未出错，这个评测机第一次把我这里卡了，一直CE，还不给出错误信息QAQ....

代码区

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = 1e9 + ;
const int Max = 1e3+ ;

struct Edge
{
    int to, next, flow;
}edge[Max << ];

int T, n, m, k;
int s, t;
vector<int>edge_raw[Max];            //记录原图边的关系
int vis[][];                //vis[i][j]记录j是否是i的前置结点
int select[];                    //记录某点是否被删除(处理工作冲突）
int use[];                        //记录每个点的是否使用（处理技能之间的前置关系）
int head[], tot;
int cost[];                        //记录了学习每个技能的花费
int val[];                        //记录掌握每个工作的报酬
int dis[];                        //记录i的层次编号（Dinic中使用）
pair<int, int>fight[];            //记录冲突

void init()
{
    s = , t = n + m + ;            //1-m为技能,m+1~n+m为工作
    memset(vis, , sizeof(vis));
    memset(use, , sizeof(use));
    for (int i = ;i <= n; i++)
        edge_raw[i].clear();
}

void add(int u, int v, int flow)
{
    edge[tot].to = v;
    edge[tot].flow = flow;
    edge[tot].next = head[u];
    head[u] = tot++;

    edge[tot].to = u;
    edge[tot].flow = ;
    edge[tot].next = head[v];
    head[v] = tot++;
}

void dfs(int u)                            //找到每个技能所有的前置技能
{
    use[u] = true;                        //代表u已经访问
    for (int i = ; i < edge_raw[u].size(); i++)
    {
        int v = edge_raw[u][i];
        vis[u][v] = true;
        if (!use[v])                    //自己是自己的前置结点
        {
            dfs(v);
        }
        for (int j = ;j <= n;j++)        //枚举这个点的前置结点
        {
            if (vis[v][j])                //v的前置结点是j，那么u的前置结点也是j
            {
                vis[u][j] = true;
            }
        }
    }
}

bool bfs()                                //判断连通性，将图分层次
{
    queue<int>q;
    memset(dis, -, sizeof(dis));
    dis[s] = ;
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();q.pop();

        for (int i = head[u]; i != -; i = edge[i].next)
        {
            int v = edge[i].to;
            if (dis[v] == - && edge[i].flow > )
            {
                dis[v] = dis[u] + ;
                q.push(v);
                if (v == t) return true;
            }
        }
    }
    return false;
}

int dfs(int u, int flow_in)
{
    if (u == t) return flow_in;
    int flow_out = ;                        //实际流出流量
    for (int i = head[u];i != -;i = edge[i].next)
    {
        int v = edge[i].to;
        if (dis[v] == dis[u] +  && edge[i].flow > )
        {
            int flow_part = dfs(v, min(flow_in, edge[i].flow));
            if (flow_part == )continue;    //无法形成增广路
            flow_in -= flow_part;
            flow_out += flow_part;
            edge[i].flow -= flow_part;
            edge[i ^ ].flow += flow_part;
            if (flow_in == )break;
        }
    }
    return flow_out;
}

int max_flow()
{
    int sum = ;
    while (bfs())
    {
        sum += dfs(s, inf);
    }
    return sum;
}

int main()
{
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
    freopen("output.txt", "w", stdout);
#endif
    scanf("%d", &T);
    while (T--)
    {
        scanf("%d%d%d", &n, &m, &k);
        init();
        for (int i = , num;i <= n;i++)
        {
            scanf("%d%d", cost + i, &num);
            for (int j = ;j <= num;j++)
            {
                int pre;                                //技能i的前置技能点
                scanf("%d", &pre);
                edge_raw[i].push_back(pre);                //构建直系前置技能关系
            }
        }
        for (int i = ;i <= n;i++)
        {
            if (!use[i])dfs(i);
        }

        for (int i = n + , cnt; i <= n + m;i++)        //工作编号n +1 ~n+m
        {
            scanf("%d%d", val + i, &cnt);
            while (cnt--)
            {
                int x;
                scanf("%d", &x);
                vis[i][x] = true;
                for (int j = ;j <= n;j++)
                {
                    if (vis[x][j])                        //求出工作所有的前置技能
                        vis[i][j] = true;
                }
            }
        }

        for (int i = ;i < k;i++)
        {
            scanf("%d %d", &fight[i].first, &fight[i].second);
        }
        int max_val = ;

        for (int state = ;state < ( << k);state++)    //枚举状态，对应位置为1表示选first，0表示选second
        {
            memset(select, , sizeof(select));            //0表示不删除
            memset(head, -, sizeof(head));tot = ;
            for (int i = ;i < k;i++)
            {
                if ((state >> i) & )
                {
                    select[fight[i].second] = true;        //删除second
                }
                else
                {
                    select[fight[i].first] = true;        //删除first
                }
            }
            int sum = ;                                //记录总价值
            for (int i =  + n;i <= n + m;i++)
            {
                if (select[i - n])continue;                //当前状态下不不选取的工作就不用构建与之有关的边了
                sum += val[i];
                add(s, i, val[i]);                        //由源点向可选工作构建一条容量为当前工作报酬的边
                for (int j = ;j <= n;j++)
                {
                    if (vis[i][j])
                    {
                        add(i, j, inf);                    //有工作向其所有前置技能点建一条容量为inf的边
                    }
                }
            }
            for (int i = ;i <= n;i++)                    //由所有技能向汇点构建一条容量为其花费的边
            {
                add(i, t, cost[i]);
            }
            int flow = max_flow();
            max_val = max(max_val, sum - flow);            //最大闭合子图的权值 = 所有权值为正的结点的权值之和 - 最小割（最大流）
        }
        printf("%d\n", max_val);
    }
    return ;
}

FZU 2295