BZOJ 1006 完美消除序列&最大势算法&弦图

　　K国是一个热衷三角形的国度,连人的交往也只喜欢三角原则.他们认为三角关系:即AB相互认识,BC相互认识,CA相互认识,是简洁高效的.为了巩固三角关系,K国禁止四边关系,五边关系等等的存在.所谓N边关系,是指N个人 A1A2...An之间仅存在N对认识关系:(A1A2)(A2A3)...(AnA1),而没有其它认识关系.比如四边关系指ABCD四个人 AB,BC,CD,DA相互认识,而AC,BD不认识.全民比赛时,为了防止做弊，规定任意一对相互认识的人不得在一队，国王想知道最少可以分多少支队。

子图:V'为V的子集 E'为E的子集

诱导子图:对于V' 只要在G中有边 那么在G'中同样应该有边

最大独立集:最大的一个点的子集使任何两个点不相邻——最大独立集数

最大团:点数最多的团——团数

最小染色:用最少的颜色给点染色使相邻点颜色不同——色数

最小团覆盖:用最少个数的团覆盖所有的点——最小团覆盖数

结论:  团数<=色数  最大独立集数<=最小团覆盖数

弦(Chord):连接环中不相邻的两个点的边

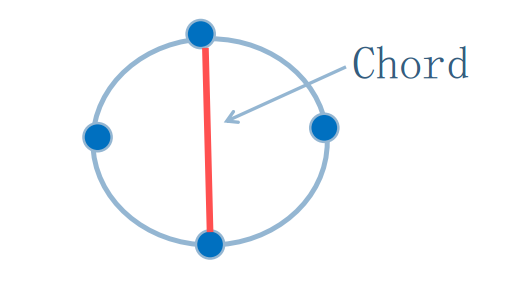
弦图:一个无向图称为弦图，当图中任意长度大于3的环都至少有一个弦

弦图的每一个诱导子图一定是弦图

弦图的判断:

ZJU1015

给定一个无向图，判定它是否为弦图

单纯点:设N(v)为与点v相邻的点的点集 一个点是单纯点当且仅当{v}+N(v)的诱导子图为一个团

引理:任何一个弦图都至少有一个单纯点  不是完全图的弦图至少有两个不相邻的单纯点

完美消除序列:

一个点的序列(每个点出现且恰好出现一次)V1,V2....Vn满足Vi在{Vi,Vi+1,Vn}的诱导子图中为一个单纯点

定理:一个无向图是弦图当且仅当它有一个完美消除序列

MCS算法O(n+m):

 #include <cstdio>
 #include <cstring>
 #include <queue>
 #include <cstdlib>
 #define N 10000 + 10
 #define M 2000000 + 10

 using namespace std;

 struct edge
 {
     int to, next;
 }e[M];
 int n, m, num, ans, maxs;
 int p[N], seq[N], col[N], lab[N], flag[N];
 struct node
 {
     int now;
     node *next;
 }f[N];//链表
 void add(int x, int y)
 {
     e[++num].to = y;
     e[num].next = p[x];
     p[x] = num;
 }
 void put(int x)
 {
     node *po = (struct node *)malloc(sizeof(struct node));
     po->next = f[lab[x]].next;
     po->now = x;
     f[lab[x]].next = po;
 }//链表的插入
 void read(int &x)
 {
     x = ;
     char c = getchar();
     while(c < '' || c > '') c = getchar();
     while(c >= '' && c <= '')
     {
         x = (x << ) + (x << ) + c - '';
         c = getchar();
     }
 }
 void init()
 {
     int x, y;
     read(n), read(m);
     for (int i = ; i <= m; ++i)
     {
         read(x), read(y);
         if (x == y) continue;
         add(x, y);
         add(y, x);
     }
 }
 void create()
 {
     for (int i = ; i <= n; ++i)
     f[i].next = NULL;//
     for (int i = ; i <= n; ++i) put(i);
     maxs = ;//初始化
     for (int i = n; i; i--)//用逆序求
     {
         node *po = f[maxs].next;//找到当前最大
         while(flag[po->now])
         {
             f[maxs].next = po = po->next;//及时删除没有用的点（漏掉的话会超时）
             while(po == NULL)
             {
                 maxs--;
                 po = f[maxs].next;
             }
         }
         f[maxs].next = po->next;//更新
         while(f[maxs].next == NULL) maxs--;
         int x = po->now;
         flag[x] = , seq[i] = x;
         for (int j = p[x]; j; j = e[j].next)
         if (!flag[e[j].to])
         {
             ++lab[e[j].to];//加势
             if (lab[e[j].to] > maxs) maxs = lab[e[j].to];
             put(e[j].to);
         }
     }
 }
 void paint()
 {
     for (int i = ; i <= n; ++i)
     flag[i] = -;
     for (int i = n; i; i--)
     {
         int x = seq[i];
         for (int j = p[x]; j; j = e[j].next)
         flag[col[e[j].to]] = i;
         for (int j = ; j <= n; ++j)
         if (flag[j] != i)
         {
             col[x] = j;
             break;
         }
         if (ans < col[x]) ans = col[x];
     }
 }
 void deal()
 {
     create();
     paint();
     printf("%d\n", ans);
 }
 int main()
 {
     //freopen("kingdom.in", "r", stdin);
     //freopen("kingdom.out", "w", stdout);
     init();
     deal();
     return ;
 }

BZOJ 1006