day 8 递归

版本1)  求5！while

 # 5! = 5*4*3*2*1
 # 4！= 4*3*2*1

 i = 1
 result = 1
 while i <= 5:
     result = result * i
     i += 1
 print(result)

版本2)  5! = 5 * 4!

####  原理  不停的调用函数   函数嵌套

 # 5! = 5 * 4！
 # 4！= 4 * 3!

 def xx(num):
     num * xxx(num-1)

 def x(num):
     num * xx(num-1)

 def get_num(num):
     num * x(num-1)

 get_num(5)

　版本3）  自身调用

 def get_num(num):
     num * get_num(num-1)

 get_num(5)

　　版本4）if判断

　　　　

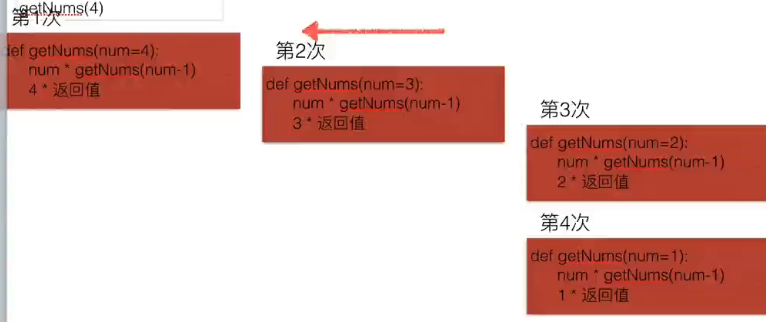
 def get_num(num):
     if num > 1:
         num * get_num(num-1)
     else:
         num

 get_num(5)

　　 版本5）return num

 def get_num(num):
     if num > 1:
         return num * get_num(num-1)
     else:
        return  num

 result = get_num(5)
 print(result)

　　　　

　　

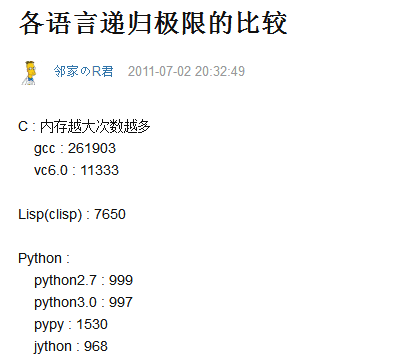
　递归的注意点：997