java递归之“二叉树”

物有本末，事有始终，知所先后，则近道矣。-----题记。

BotWong半路入行it做码农，也就半年时间，竟“不知天高地厚”地来到了深圳闯天下。一口气投了百个简历，一周后终于有公司邀约面试，除了基础的java语法和开发经验，大一点的公司都会出几道题给你做（算法题）。BotWong是一头雾水，而且心里很生气！气！气！气！以前自己学的是“人类心理学理论与实践”专业，唯一的计算机基础也就是用过word、excel给客户报过价。自己硬着头皮把java语法和javaEE框架学了一遍，像我这样的个例已经算是出类拔萃的了，为什么还要对我这么苛刻，哼！BotWong从那以后就开始讨厌那些喜欢考试的公司，并发誓以后再也不去那样的公司面试！

我和BotWong是好朋友，他提出了自己的困惑：到底要不要学这些看着“没用”的算法，问我该怎么看待这件事，该如何做。好在BotWang还是个头脑清醒的人，要不然也不会问这样的问题了。我看他挺有诚意，就把自己以前写的一些代码，其中就包含一些算法，拿出来泛泛地说了一遍，建议他自己都去实现一遍。BotWang消失了三月，再见之时，已能感知其功力大涨，已非三月前的那个BotWong了。我心甚慰，特此将自己以前写过的集合类都贴出来，方便自己和网上的宝宝们随时翻看，随时补充能量。

一、二叉树类：

package tree;
/**
 * 二叉树数据载体类
 * @author tery
 *
 * @param <T>
 */
public class BinaryTreeNode<T> {
    private T data;//权值
    private BinaryTreeNode<T> left;//左孩子
    private BinaryTreeNode<T> right;//右孩子
    public BinaryTreeNode(T data){
        this.data=data;
        left=right=null;
    }
    public T getData(){
        return this.data;
    }
    public void setData(T data){
        this.data=data;
    }
    public BinaryTreeNode<T> getLeft() {
        return left;
    }
    public void setLeft(BinaryTreeNode<T> left) {
        this.left = left;
    }
    public BinaryTreeNode<T> getRight() {
        return right;
    }
    public void setRight(BinaryTreeNode<T> right) {
        this.right = right;
    }
　　/**
　　*插入权值
　　*/
    @SuppressWarnings("unchecked")
    public BinaryTreeNode<T> insert(BinaryTreeNode<T> node,Integer data){
        if(node==null){
            return new BinaryTreeNode<T>((T)data);
        }
　　　　//如果当前节点的权值大于data，那么插入到左孩子节点上
        if(Integer.valueOf(node.getData().toString())>data){
            node.left=insert(node.getLeft(),data);
        }
　　　//如果当前节点的权值大于data，那么插入到左孩子节点上
　　　　if(Integer.valueOf(node.getData().toString())<data){ node.right=insert(node.getRight(),data); } 

　　　　//相等抛异常 
　　　　if(Integer.valueOf(node.getData().toString())==data){
 　　　　throw new IllegalArgumentException("the data:"+data+"is already exsist in the tree"); 
　　　　} 
　　　　return node;
 } 
}

insert方法中涉及到的递归：

        : aload_1
        : ifnonnull
        : new           #                  // class tree/BinaryTreeNode
        : dup
        : aload_2
        : invokespecial #                 // Method "<init>":(Ljava/lang/Object;)V
        : areturn
        : aload_1
        : getfield      #                 // Field data:Ljava/lang/Object;
        : aload_2
        : if_icmple
        : getfield      #                 // Field left:Ltree/BinaryTreeNode;
        : aload_2
        : invokevirtual #                 // Method insert:(Ltree/BinaryTreeNode;Ljava/lang/Object;)Ltree/BinaryTreeNode;
        : putfield      #                 // Field left:Ltree/BinaryTreeNode;
        : aload_1
        : areturn

上面是insert方法的jvm执行的指令，我摘抄了部分关键点说明一下递归是怎么做的：

insert函数栈中的局部变量表中的参数：第一个是当前树节点对象（暂且称为ref0），第二个是函数中传进来的node对象的引用（称为ref1），第三个是传进来的常量data（在常量池中#20）

0: aload_1 将第一个引用类型局部变量推送至栈顶，那个引用也就是insert方法中的node对象的引用（ref1）

1 : ifnonnull 13 如果ref1不为空，则跳到13行执行

4-12 : 如果是空，则此节点即是我们要插入的节点，调用它的构造函数<init>方法，将data值赋给它，然后areturn（将这个新生成的对象引用返回）

13 : aload_1 将ref1压入栈顶

14：getfield  将常量池中当前对象ref1的data的值压入栈顶

23：aload_2 将传入的data值压入栈顶

30：if_icmple 79，如果传入的data值小于ref1的权值，那么就跳到79执行

36：getfield #24 ，将常量池中#24，即left压入栈中，即left常量的引用

39：aload_2 将data值压入栈中。实际上36、39两步的指令都是在为下面40行做准备，40行调用insert方法，传递给它需要的参数

40：invokevirtrual #53，调用insert方法，将36、39行准备的两个参数带过去

43：putfield #24 ，给当前实例ref1的left字段赋值

79：aload_1 ，将当前实例ref1压入栈中

80：areturn ，将栈顶的ref1返回

如果你不太懂，我还给你画了个图，帮助你理解：

假设jvm只执行了在左边树插入的递归步骤：

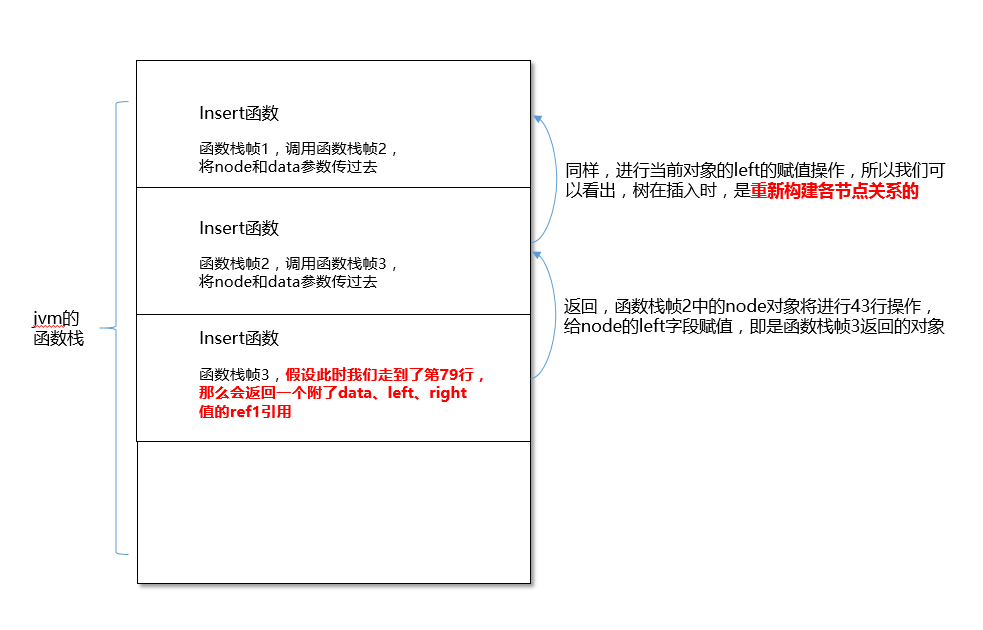
上面的字节码指令和图解是截取了部分关键点进行讲解的，如果想进一步探讨的宝宝们，可以联系我详细讨论。

三、二叉树工具类：

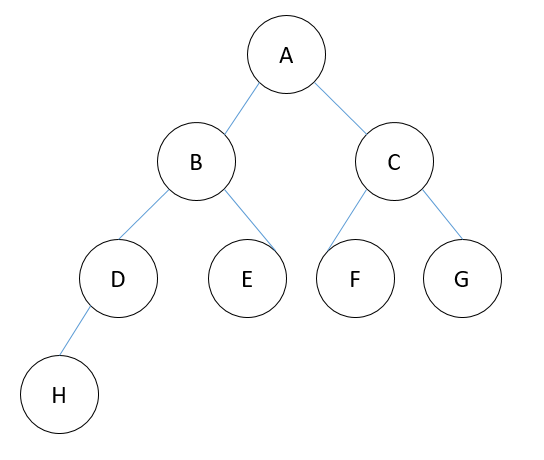
1. 前根序遍历：先遍历根结点，然后遍历左子树，最后遍历右子树。（ABDHECFG）

2.中根序遍历：先遍历左子树，然后遍历根结点，最后遍历右子树。（HDBEAFCG）

3.后根序遍历：先遍历左子树，然后遍历右子树，最后遍历根节点（HDEBFGCA）

package tree;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class BinaryTreeUtil {

    /**
     * 用递归的方式实现二叉树的前序遍历
     * @param root
     * @return
     */
    public static<T> List<T> preOrderVisit(BinaryTreeNode<T> root){
        List<T> result=new ArrayList<>();
        preOrderVisit(root,result);
        return result;
    }
    private static<T> void preOrderVisit(BinaryTreeNode<T> node, List<T> result) {
        //如果节点为空，返回
        if(node==null){
            return;
        }
        //不为空，则加入节点的值
        result.add(node.getData());
        //先递归左孩子
        preOrderVisit(node.getLeft(),result);
        //再递归右孩子
        preOrderVisit(node.getRight(),result);
    }
    /**
     * 用递归的方式实现二叉树的中序遍历
     * @param root
     * @return
     */
    public static<T> List<T> inOrderVisit(BinaryTreeNode<T> root){
        List<T> result=new ArrayList<T>();
        inOrderVisit(root,result);
        return result;
    }
    private static<T> void inOrderVisit(BinaryTreeNode<T> node, List<T> result) {
        if(node==null){
            return;
        }
        inOrderVisit(node.getLeft(),result);
        result.add(node.getData());
        inOrderVisit(node.getRight(),result);
    }
    /**
     * 用递归的方式实现二叉树的后遍历
     * @param root
     * @return
     */
    public static<T> List<T> postOrderVisit(BinaryTreeNode<T> root){
        List<T> result=new ArrayList<T>();
        postOrderVisit(root,result);
        return result;
    }
    private static<T> void postOrderVisit(BinaryTreeNode<T> node, List<T> result) {
        if(node==null){
            return;
        }
        postOrderVisit(node.getLeft(),result);
        postOrderVisit(node.getRight(),result);
        result.add(node.getData());
    }
    /**
     * 用非递归的方式实现前序遍历
     * @param root
     * @return
     */
    public static<T> List<T> preOrderVisitWithoutRecursion(BinaryTreeNode<T> root){
        List<T> result=new ArrayList<T>();
        Stack<BinaryTreeNode<T>> stack=new Stack<>();
        if(root!=null){
            stack.push(root);
        }
        while(!stack.isEmpty()){
            BinaryTreeNode<T> node=stack.pop();
            result.add(node.getData());
            if(node.getRight()!=null){
                stack.push(node.getRight());
            }
            if(node.getLeft()!=null){
                stack.push(node.getLeft());
            }
        }
        return result;
    }
    /**
     * 用非递归的方式实现中序遍历
     * @param root
     * @return
     */
    public static<T> List<T> inOrderVisitWithoutRecursion(BinaryTreeNode<T> root){
        List<T> result=new ArrayList<T>();
        Stack<BinaryTreeNode<T>> stack=new Stack<>();
        BinaryTreeNode<T> node=root;
        while(node!=null || !stack.isEmpty()){
            while(node!=null){
                stack.push(node);
                node=node.getLeft();
            }
            BinaryTreeNode<T> currentNode=stack.pop();
            result.add(currentNode.getData());
            node=currentNode.getRight();
        }
        return result;
    }

二叉树部分上面总共列举了15个方法，主要的思想还是用递归。关于递归，为了让宝宝们明白是怎么回事，我也是花了点心思去解释的，请各位再深入思考一下。里面涉及到了jvm函数调用层面的知识，如果不懂，建议大家去看看jvm的书，了解jvm怎么执行代码，那就可以轻轻松松地理解递归到底是怎么执行的了。