B+树全面解析

B+树的特征与结构

有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素

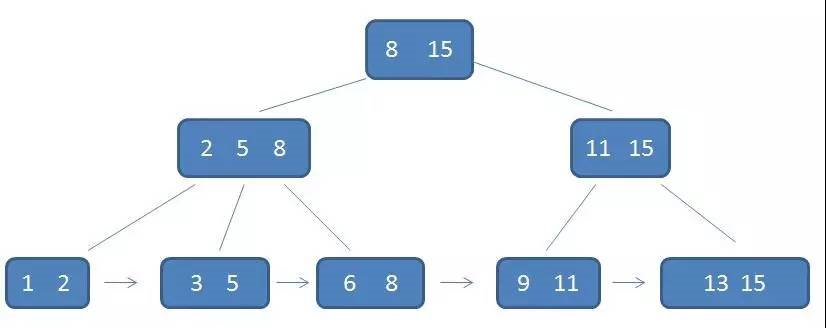
　　从上图可以看出，不但节点之间含有重复元素，而且叶子结点还用指针连接在一起。这正是B+数的几个特征，首先，每个元素都出现子节点中，是子节点的最大（或者最小）元素。

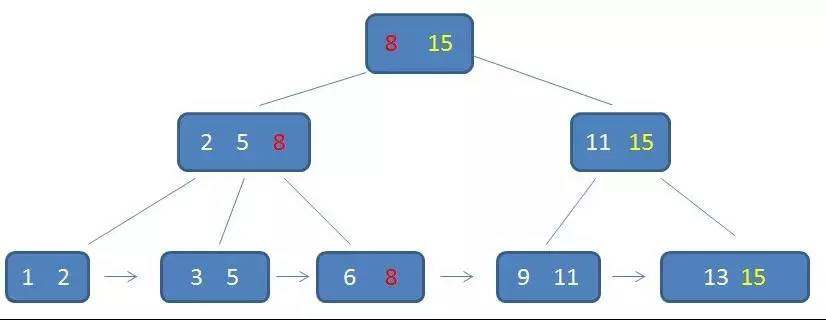
　　在上面这课树中，根节点元素8是子节点2，5，8的最大元素，也是叶子节点6，8的最大元素。需要注意的是根节点的最大元素（这里是15），也就等同于整个B+树的最大元素。以后无论插入删除多少元素，始终保持最大元素在根节点当中。

　　至于叶子节点，由于父节点的元素都出现在子节点，因此叶子结点包含了全部元素的信息。并且每个叶子节点都带有指向下一个节点的指针，形成了一个有序链表。

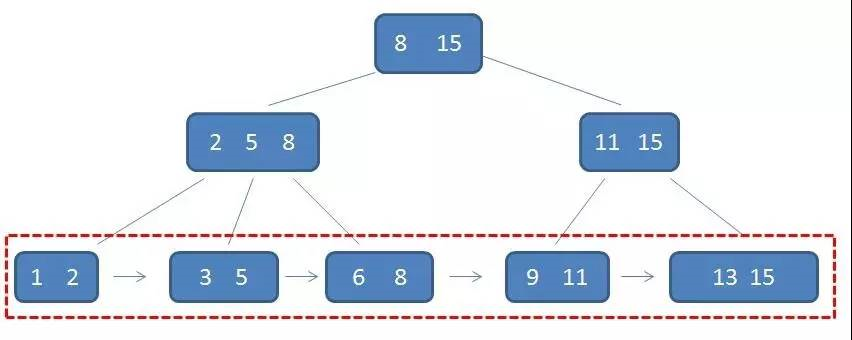
　　B+树还具有一个重要的特点，这个特点是在索引之外，确实至关重要的特点。那就是【卫星数据】，

　　所谓卫星数据，指的就是索引元素所指向的数据记录，比如数据库中的某一行。在B-树中，无论是中间节点还是叶子结点都带有卫星数据，而在B+树当中，只有叶子节点带有卫星数据，其余中间节点仅仅是索引，没有任何数据关联。

B-树中的卫星数据（Satellite Information）：

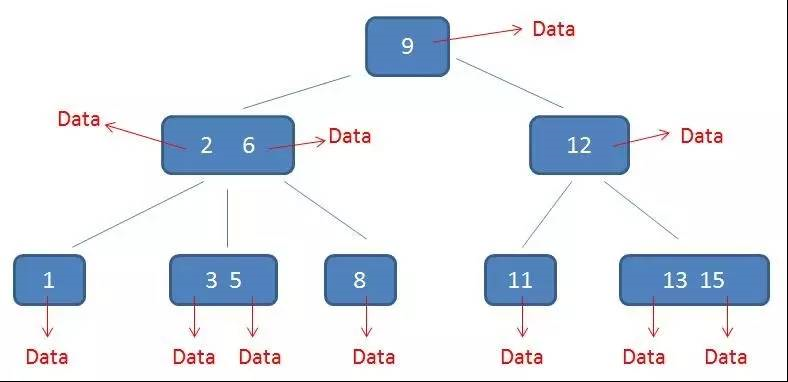
B+树中的卫星数据（Satellite Information）：

需要补充的是，在数据库的聚集索引（Clustered Index）中，叶子节点直接包含卫星数据。在非聚集索引（NonClustered Index）中，叶子节点带有指向卫星数据的指针。

聚集索引和非聚集索引详细请点

B+树的优点

　　B+树的好处主要体现在查询性能上。下面我们可以通过单行查询和范围查询来做分析。

　　在单元素查询的时候，B+树会自顶向下逐层查找节点，最终找到匹配的叶子节点。

第一次磁盘IO

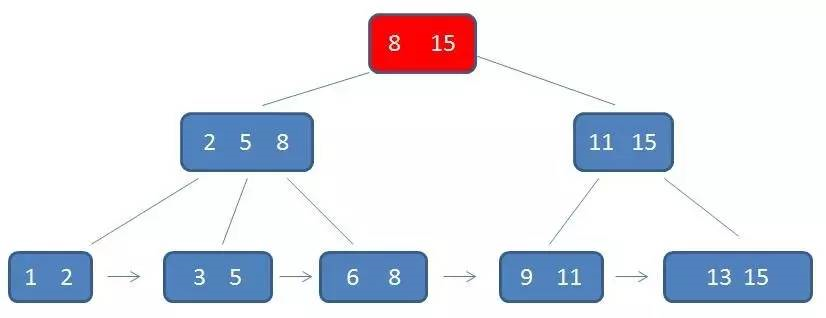
第二次磁盘IO

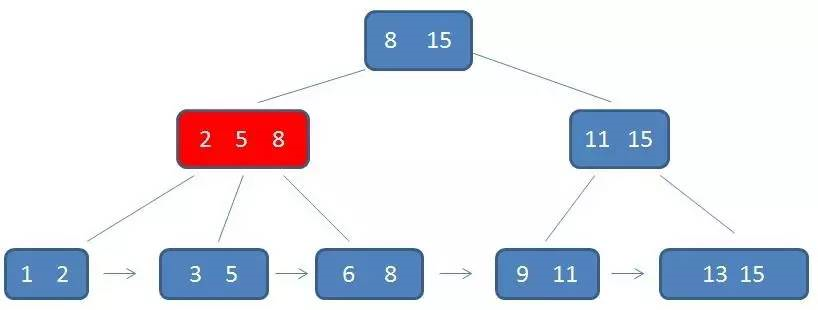
第三次磁盘IO

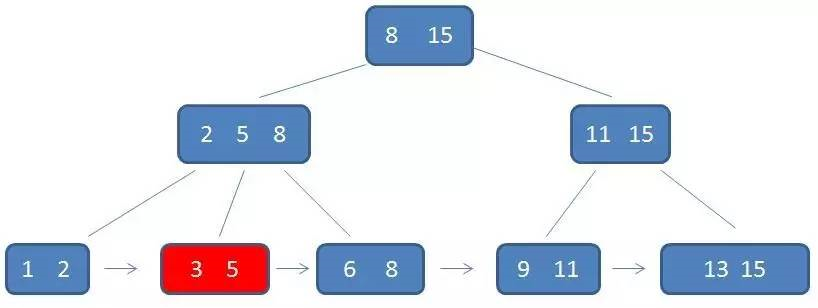
优点：

B+树的中间节点没有卫星数据，所以同样大小的磁盘页可以容纳更多的节点元素，这就意味着在数据量相同的情况下，B+树更加的矮胖，因此IO的次数也就较少
B+树查询必须查找到叶子节点，每一次查找都是稳定的

B-树的范围查找及过程与B+树对比
自顶向下,查找到范围的下限(3)

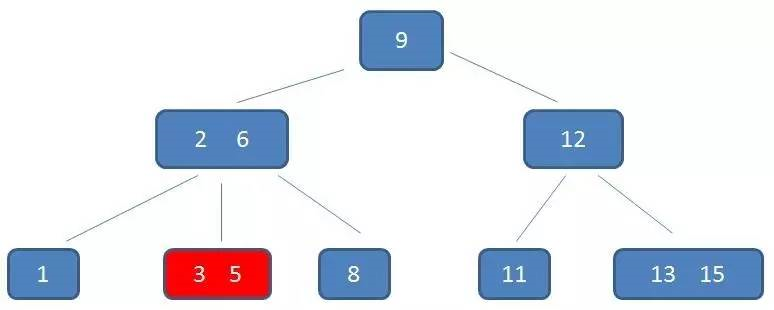
中序遍历到元素6

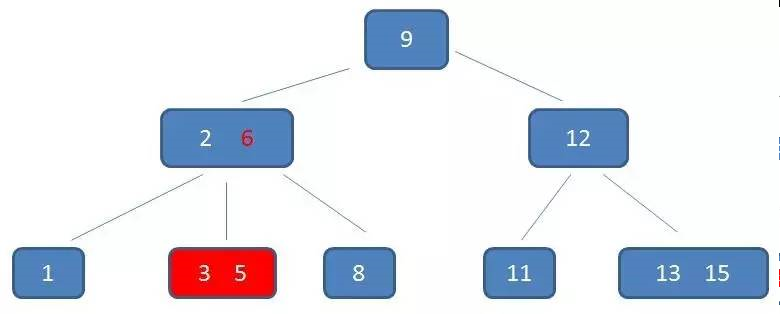
中序遍历到元素8

中序遍历到元素9

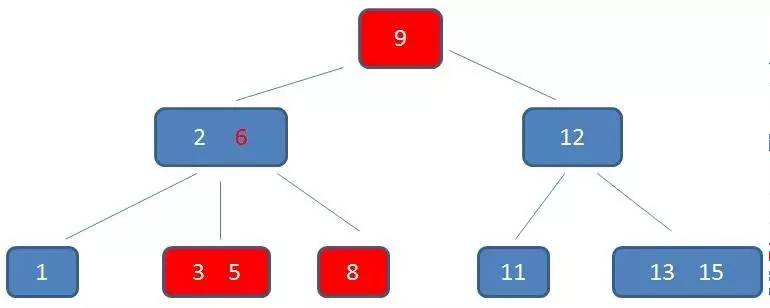
中序遍历到元素11

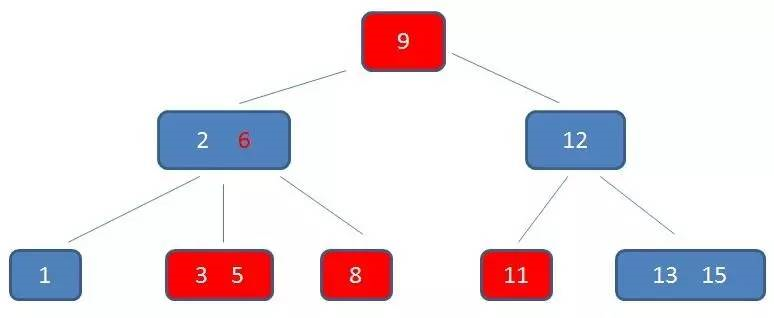
B+树的范围查找过程
自顶向下,查找到范围的下限(3)

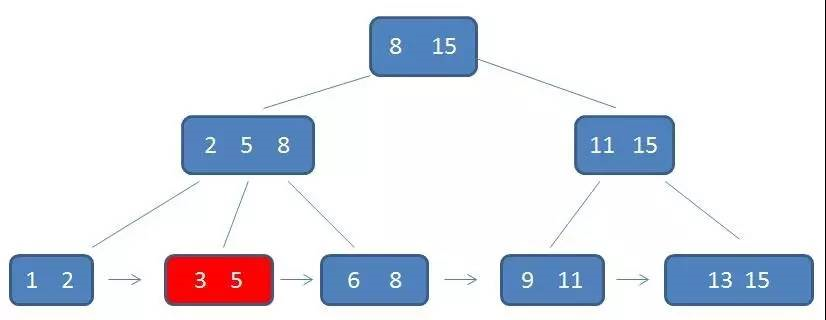
通过链表指针,遍历到元素6,8

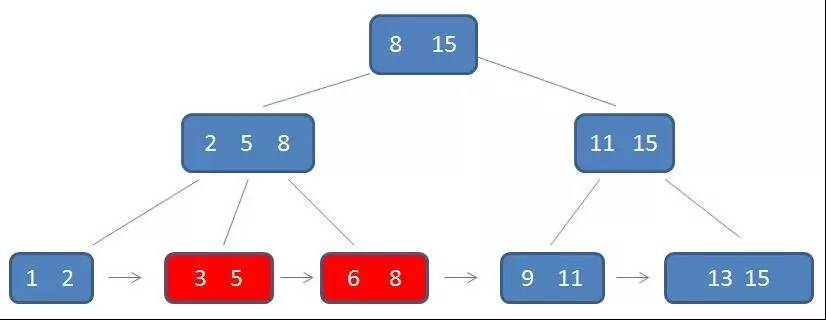
通过链表指针,遍历到元素9,11,遍历结束

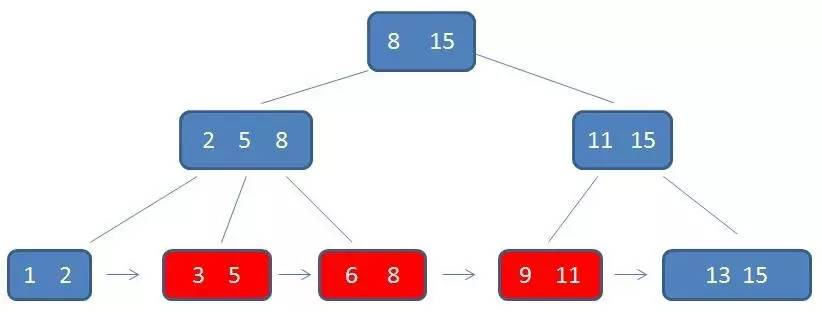
综合来说

　　 B+树的优势：
　　　　1.单一节点存储更多的元素，使得查询的IO次数更少。
　　　　2.所有查询都要查找到叶子节点，查询性能稳定。
　　　　3.所有叶子节点形成有序链表，便于范围查询,远远高于B-树