codeforces 200 div2 C. Rational Resistance 思路题

C. Rational Resistance

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.

However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:

1. one resistor;
2. an element and one resistor plugged in sequence;
3. an element and one resistor plugged in parallel.

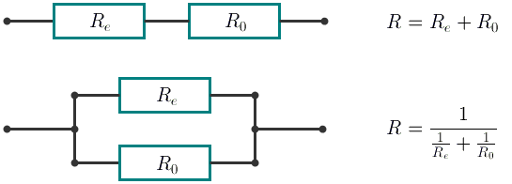
With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals 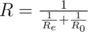. In this case Re equals the resistance of the element being connected.

Mike needs to assemble an element with a resistance equal to the fraction . Determine the smallest possible number of resistors he needs to make such an element.

Input

The single input line contains two space-separated integers a and b (1 ≤ a, b ≤ 1018). It is guaranteed that the fraction  is irreducible. It is guaranteed that a solution always exists.

Output

Print a single number — the answer to the problem.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%I64d specifier.

Examples

input

1 1

output

1

input

3 2

output

3

input

199 200

output

200

Note

In the first sample, one resistor is enough.

In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance 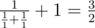. We cannot make this element using two resistors.

题意：要得到a/b的电阻最小需要多少个电阻；（注意：每次只能串联一个或者并联一个）；

思路：每次串联一个得到（a+b）/a，并联一个得到a/(a+b);

#include<bits/stdc++.h>
using namespace std;
#define ll __int64
#define mod 1000000007
#define inf 100000000000005
#define MAXN 10000010
//#pragma comment(linker, "/STACK:102400000,102400000")
int main()
{
    ll x,y,z,i,t;
    scanf("%I64d%I64d",&x,&y);
    ll ans=;
    while()
    {
        if(x>y)
        {
            ans+=x/y;
            x%=y;
            if(x==)
            break;
        }
        else if(x<y)
        {
            z=x;
            x=y-x;
            y=z;
            ans++;
        }
        else
        {
            ans+=;
            break;
        }
    }
    cout<<ans<<endl;
    return ;
}