第二章平稳时间序列模型——AR(p),MA(q),ARMA(p,q)模型及其平稳性






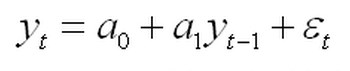


 等于
等于
 等于
等于


 或
或 )
)模型表达式为:(2.16)(截距项不影响平稳性,略去)
设其挑战解为:(用待定系数法)
 (2.17)
(2.17)


 (t很大时用级数求和)
(t很大时用级数求和) 等于
等于

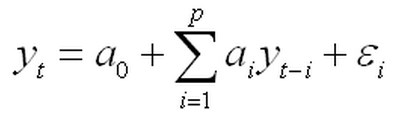




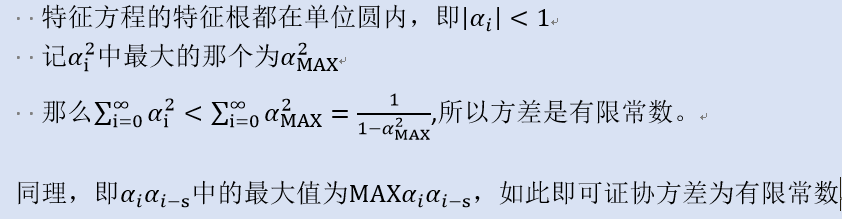
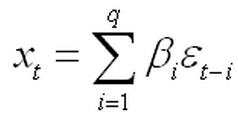


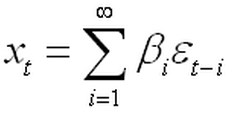

 (2.22)
(2.22) (2.23)
(2.23) 的特征根在单位圆外,则(2.23)的每一项都平稳,所以其和也平稳,所以ARMA(p,q)模型平稳。(书上没再给出更多解释了)
的特征根在单位圆外,则(2.23)的每一项都平稳,所以其和也平稳,所以ARMA(p,q)模型平稳。(书上没再给出更多解释了)第二章平稳时间序列模型——AR(p),MA(q),ARMA(p,q)模型及其平稳性的更多相关文章
- 第二章平稳时间序列模型——ACF和PACF和样本ACF/PACF
自相关函数/自相关曲线ACF AR(1)模型的ACF: 模型为: 当其满足平稳的必要条件|a1|<1时(所以说,自相关系数是在平稳条件下求得的): y(t)和y(t-s)的 ...
- 时间序列算法(平稳时间序列模型,AR(p),MA(q),ARMA(p,q)模型和非平稳时间序列模型,ARIMA(p,d,q)模型)的模型以及需要的概念基础学习笔记梳理
在做很多与时间序列有关的预测时,比如股票预测,餐厅菜品销量预测时常常会用到时间序列算法,之前在学习这方面的知识时发现这方面的知识讲解不多,所以自己对时间序列算法中的常用概念和模型进行梳理总结(但是为了 ...
- ARIMA模型——本质上是error和t-?时刻数据差分的线性模型!!!如果数据序列是非平稳的,并存在一定的增长或下降趋势,则需要对数据进行差分处理!ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数
https://www.cnblogs.com/bradleon/p/6827109.html 文章里写得非常好,需详细看.尤其是arima的举例! 可以看到:ARIMA本质上是error和t-?时刻 ...
- ASP.NET MVC with Entity Framework and CSS一书翻译系列文章之第二章:利用模型类创建视图、控制器和数据库
在这一章中,我们将直接进入项目,并且为产品和分类添加一些基本的模型类.我们将在Entity Framework的代码优先模式下,利用这些模型类创建一个数据库.我们还将学习如何在代码中创建数据库上下文类 ...
- 《Entity Framework 6 Recipes》翻译系列 (3) -----第二章 实体数据建模基础之创建一个简单的模型
第二章 实体数据建模基础 很有可能,你才开始探索实体框架,你可能会问“我们怎么开始?”,如果你真是这样的话,那么本章就是一个很好的开始.如果不是,你已经建模,并在实体分裂和继承方面感觉良好,那么你可以 ...
- 【黑金原创教程】【TimeQuest】【第二章】TimeQuest模型角色,网表概念,时序报告
声明:本文为黑金动力社区(http://www.heijin.org)原创教程,如需转载请注明出处,谢谢! 黑金动力社区2013年原创教程连载计划: http://www.cnblogs.com/al ...
- 时序分析:ARIMA模型(非平稳时间序列)
转载于一篇硕士论文.... ARIMA模型意为求和自回归滑动平均模型(IntergratedAut少regressive MovingAverageModel),简记为ARIMA(p,d,q),p,q ...
- [书籍翻译] 《JavaScript并发编程》 第二章 JavaScript运行模型
本文是我翻译<JavaScript Concurrency>书籍的第二章 JavaScript运行模型,该书主要以Promises.Generator.Web workers等技术来讲解J ...
- KnockoutJS 3.X API 第二章 数据监控(1)视图模型与监控
数据监控 KO的三个内置核心功能: 监控(Observable)和依赖性跟踪(dependency tracking) 声明绑定(Declarative bindings) 模板(Templating ...
随机推荐
- Unity 依赖注入知识点
三种依赖注入方法,构造器注入.属性注入.方法注入 可以配置Config文件,来实现不用修改代码.需要先将接口与实体关联,然后使用时会自动加载对应实体. namespace WeChatConsole ...
- 旅图beta版 asp.net web api 单元测试
旅图 beta版 asp.net web api 单元测试 测试接口:http://120.27.7.115:1010/Help 测试目的 对每个接口单元进行测试,保证每个接口的可靠性. 单元描述 注 ...
- CSS--值和单位
等价颜色表 什么叫Web安全色 所谓的“web安全”颜色是指在256色计算机系统上总能避免抖动的颜色. Web安全颜色可以表示为RGB值为20%和51(相应的十六进制值为33)的倍数. 如果使用RGB ...
- JavaScript杂谈(顺便也当知识积累)
JavaScript版本 JavaScript的普及使得其于1997年正式成为国际标准,其官方名称为ECMAScript 1999年定稿第三版ECMAScript标准,简称ES3 2009年重大改进的 ...
- MFC学习-第2,3课 MFC框架的运行机制
转自:http://blog.163.com/zhigang0633@126/blog/static/38790491200822711526168/ 讲述MFC AppWizard的原理与MFC程序 ...
- C#--API
C#中调用API 介绍 API( Application Programming Interface ),我想大家不会陌生,它是我们Windows编程的常客,虽然基于.Net平台的C#有了强大的类库, ...
- 自然语言20_The corpora with NLTK
QQ:231469242 欢迎喜欢nltk朋友交流 https://www.pythonprogramming.net/nltk-corpus-corpora-tutorial/?completed= ...
- Java关键字——final
final在Java中表示的意思是最终,使用final关键字声明类属性.方法,注意: 1.使用final声明的类不能有子类 2.使用final声明的方法不能被子类所覆写 3.使用final声明的变量即 ...
- EF--Codefirst 加密数据库连接字符串
http://www.tuicool.com/articles/QvYbEn 一.EF,CodeFirst加密SQL连接符 public LifeHelpContext() : base(" ...
- linq group join
本篇介绍Linq的Group和Join操作,继续使用<Linq 学习(3) 语法结构>中介绍的数据源. GroupGroup是进行分组操作,同SQL中的Group By类似.原型如下: p ...
