JavaScript实现栈结构

参考资料

一.什么是栈（stack）？

1.1.简介

首先我们需要知道数组是一种线性结构，并且可以在数组的任意位置插入和删除数据，而栈（stack）是一种受限的线性结构。以上可能比较难以理解，什么是受限制的线性结构？让我们首先来了解下栈结构的特点吧，下面就是栈的图解：



总结栈的特点就是在放入数据的过程中是先进后出，后进后出（LIFO：last in first out）

1.2.程序中的栈实现

• 函数调用栈：A（B（C（D））），既A函数中调用B，B调用C，C调用D；在A执行的过程中将A压入栈，随后B执行时B也被压入栈，同理C和D执行时也会被压入栈。所有当前栈的顺序是：A->B->C->D（栈顶）；同时D因为在栈顶，在先执行完后，会弹出栈被释放，因此弹出栈的顺序为：D->C->B->A

• 递归:为什么说递归也是栈的实现方式呢？因为在递归的使用时如果未设置停止递归的条件就会造成栈溢出！因为递归也是的调用自身就是一种函数调用栈，因此如果未停止，会一直调用自身，不会把函数弹出栈，不停的将函数压入栈，最好造成栈溢出！（Stack OverFloat）

1.3.一道面试题理解栈结构

首先我们来分析题目：六个元素顺序进栈，注意只是顺序进栈,并没有说是同时进入哟,可能有进有出，如果同时岂不是考的太简单了？哈哈，是不是嘛，所有我们要根据答案来一一判断。

• A：65进栈-5出栈-4进栈出栈-3进栈出栈-6出栈-21进栈（符合入栈顺序654321）
• B：654进栈-4出栈-5出栈-3进栈出栈-2进栈出栈-1进栈出栈-6出栈（符合）
• C：6543进栈-3出栈-4出栈-6出栈（此处不符合，理论上不应该是6,6上面还有5未出栈）
• D：65432进栈-2出栈-3出栈-4出栈-1进栈出栈-5出栈-6出栈（符合）

综上所述，答案是 C

二.栈结构实现

2.1.栈的封装

首先我们先需了解栈常见的操作有哪些？

• push(element): 添加一个新元素到栈顶位置.
• pop()：移除栈顶的元素，同时返回被移除的元素。
• peek()：返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它）。
• isEmpty()：如果栈里没有任何元素就返回true，否则返回false。
• clear()：移除栈里的所有元素。
• size()：返回栈里的元素个数。这个方法和数组的length属性很类似。

封装代码如下：

// 封装栈类
      function Stack() {
        // 栈中的属性
        this.items = []

        // 栈的相关操作
        // 1.将元素压入栈
        Stack.prototype.push = function (element) {
          this.items.push(element)
        }

        // 2.从栈中取出元素
        Stack.prototype.pop = function () {
          return this.items.pop()
        }

        // 3.查看一下栈顶元素
        Stack.prototype.peek = function () {
          return this.items[this.items.length - 1]
        }

        // 4.判断栈是否为空
        Stack.prototype.isEmpty = function () {
          return this.items.length == 0
        }

        // 5.获取栈中元素的个数
        Stack.prototype.size = function () {
          return this.items.length
        }

        // 6.toString方法
        Stack.prototype.toString = function () {
          // 形式自定 1 2 3 4 5
          var resultString = ''
          this.items.forEach((element) => {
            resultString += element + ' '
          })
          return resultString
        }
      }

测试代码：

      // 栈的使用
      var s = new Stack()
      s.push(1)
      s.push(2)
      s.push(3)
      s.push(4)
      console.log(s.items) // [1,2,3,4]
      s.pop()
      console.log(s.items) // [1,2,3]
      console.log(s.peek()) // 3
      console.log(s.isEmpty()) // false
      console.log(s.size()) // 3
      console.log(s.toString()) // 1 2 3 (String)

2.2.栈结构的简单应用（十进制转二进制）

首先你必须要理解十进制转二进制的方法，除以二取余，一直除到结果为0为止。举个例子吧，把10进制的数字10转换为二进制的数字，过程大概是如下流程：



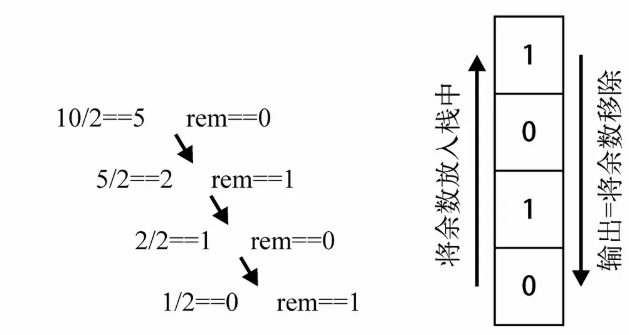
结果就是1010，就是将余数类似栈的方式依次取出来。

• 如果我们希望通过代码来实现这个过程呢？

      // 封装十进制转二进制的函数
      function dec2bin(decNumber) {
        // 1.定义栈对象，上文封装的栈类
        var stack = new Stack()
        // 2.循环操作
        while (decNumber > 0) {
          // 2.1获取余数，并且放入栈中
          stack.push(decNumber % 2)
          // 2.2更新decNumber，获取整除后的结果，作为下一次运行的数字
          decNumber = Math.floor(decNumber / 2)
        }
        // 3.从栈中取出0和1
        let binaryString = ''
        while (!stack.isEmpty()) {
          binaryString += stack.pop()
        }
        return binaryString
      }

测试代码:

      // 测试代码
      console.log(dec2bin(10)) //1010
      console.log(dec2bin(100)) //1100100

三.总结

看完是否对栈结构有一个清晰的了解？记住后进先出（LIFO：last farst in out）！