@codeforces - 575E@ Spectator Riots

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

一个以 (0, 0) 为左下角，(10^5, 10^5) 为右上角的球场中有 n 个人，第 i 个人在 (xi, yi) 上，并有速度 vi。

在 1s 后，每个人会等概率地移动到与原位置的曼哈顿距离 <= v 的地方（不会移动到界外）。

你需要选取三个位置（满足这些位置在 1s 后可能出现人），然后过这三点作圆。

请选取在初始状态 1s 后圆内人数的期望值最大的方案输出。如果有多种，输出半径最大的方案。

原题题面。

@solution@

首先根据最小圆覆盖那一套理论（或者你乱猜都猜得到），存在一个圆经过给定点集的三个点，覆盖整个点集。

那么这道题的最大期望值就是骗人的 = =。

我们可以先对原始点集求一个凸包，再在凸包上作圆。

首先注意到，半径最大的圆一定包含整个凸包。否则我可以搞出一个半径更大的圆。

为了分析，我们随便画一个如图的凸包：

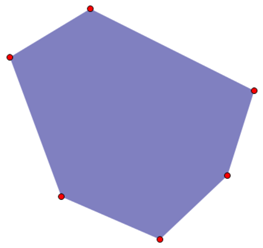
再随便钦定两个必须在圆上的点，则圆心在它们的中垂线上移动。随便找一个合适的圆：

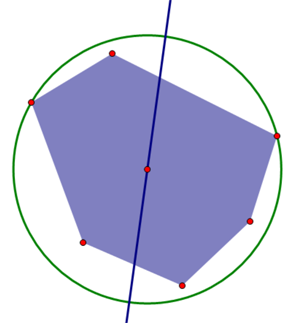
注意到此时我可以将圆心上移或者下移，使得凸包与圆相切。

因为圆心向下移动一定会在某刻切中上面的点，向上移动一定会在某刻切中下面的点，所以经过两个点的圆最多出现两种情况。

而根据圆心的位置，上移和下移必然有一个对应半径是单调增大的。

但是假如这两个顶点相邻，则上移和下移中只会有一个情况会切到凸包。

那么假如我选取的圆在凸包上的三个点 A, B, C 不相邻，必然可以从三个点选择两个点 P, Q（只要这两个点之间的边 PQ 对应的角是锐角），使得以 P, Q 作中垂线，把圆心往另一个方向挪，半径会单调增大。

也就是说，这道题求出凸包过后只需要求凸包上三个相邻点对应的半径最大的外切圆 = =。

三角形外切圆的半径可以用正弦公式得到为 \(R = \frac{a*b*c}{4*S}\)。

@accepted code@

#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define border(p) (0 <= p.x && p.x <= 1E5 && 0 <= p.y && p.y <= 1E5)
#define inside(p, v, x) (fabs(x.x - p.x) + fabs(x.y - p.y) <= v)
const int MAXN = int(1E6);
const double INF = 1E10;
const double EPS = 1E-9;
int dcmp(double x) {return fabs(x) <= 0 ? 0 : (x > 0 ? 1 : -1);}
struct point{
	double x, y;
	point() : x(), y() {}
	point(double _x, double _y) : x(_x), y(_y) {}
	friend point operator + (point a, point b) {return point(a.x + b.x, a.y + b.y);}
	friend point operator - (point a, point b) {return point(a.x - b.x, a.y - b.y);}
	friend point operator * (point a, double k) {return point(a.x * k, a.y * k);}
	friend point operator / (point a, double k) {return point(a.x / k, a.y / k);}
	friend double operator * (point a, point b) {return a.x*b.x + a.y*b.y;}
	friend double operator ^ (point a, point b) {return a.x*b.y - a.y*b.x;}
	friend bool operator < (point a, point b) {return (a.x == b.x ? a.y < b.y : a.x < b.x);}
	friend bool operator == (point a, point b) {return (a.x == b.x) && (a.y == b.y);}
	friend double length(point a) {return sqrt(a * a);}
	friend double dist(point a, point b) {return length(a - b);}
	friend double area(point a, point b, point c) {return ((c - a) ^ (b - a)) / 2;}
	friend double slope(point a, point b) {
		if( a.x == b.x ) return a.y < b.y ? INF : -INF;
		else return 1.0*(a.y - b.y)/(a.x - b.x);
	}
	friend void read(point &a) {scanf("%lf%lf", &a.x, &a.y);}
};
point stk[MAXN + 5], t[MAXN + 5], a[MAXN + 5];
int siz, cnt, tp;
void convex() {
	sort(a + 1, a + cnt + 1);
	stk[tp = 1] = a[1];
	for(int i=2;i<=cnt;i++) {
		if( a[i] == a[i-1] ) continue;
		while( tp >= 2 && slope(stk[tp-1], stk[tp]) <= slope(stk[tp], a[i]) )
			tp--;
		stk[++tp] = a[i];
	}
	for(int i=1;i<=tp;i++)
		t[++siz] = stk[i];
	stk[tp = 1] = a[1];
	for(int i=2;i<=cnt;i++) {
		if( a[i] == a[i-1] ) continue;
		while( tp >= 2 && slope(stk[tp-1], stk[tp]) >= slope(stk[tp], a[i]) )
			tp--;
		stk[++tp] = a[i];
	}
	for(int i=tp-1;i>=2;i--)
		t[++siz] = stk[i];
}
int nxt(int x) {return (x == siz ? 1 : x + 1);}
void print(point p) {printf("%.0f %.0f\n", p.x, p.y);}
void solve() {
	convex();
	double r = 0; int p = 0;
	for(int i=1;i<=siz;i++) {
		int j = nxt(i), k = nxt(j);
		double r1 = dist(t[i],t[j])*dist(t[i],t[k])*dist(t[j],t[k])/(4*area(t[i],t[j],t[k]));
		if( dcmp(r1 - r) > 0 ) p = i, r = r1;
	}
	print(t[p]), p = nxt(p);
	print(t[p]), p = nxt(p);
	print(t[p]), p = nxt(p);
}
void update1(point p) {
	if( border(p) ) a[++cnt] = p;
}
void update2(point p, double v, point x) {
	if( inside(p, v, x) ) a[++cnt] = x;
}
int main() {
	int n; scanf("%d", &n);
	for(int i=1;i<=n;i++) {
		double x, y, v; scanf("%lf%lf%lf", &x, &y, &v);
		point p = point(x, y);
		update1(point(x + v, y)), update1(point(x - v, y));
		update1(point(x, y + v)), update1(point(x, y - v));
		if( x - v < 0 ) update1(point(0, y + (v - x))), update1(point(0, y - (v - x)));
		if( y - v < 0 ) update1(point(x + (v - y), 0)), update1(point(x - (v - y), 0));
		if( x + v > 1E5 ) update1(point(1E5, y + (v - (1E5 - x)))), update1(point(1E5, y - (v - (1E5 - x))));
		if( y + v > 1E5 ) update1(point(x + (v - (1E5 - y)), 1E5)), update1(point(x - (v - (1E5 - y)), 1E5));
		update2(p, v, point(0, 0)), update2(p, v, point(1E5, 1E5));
		update2(p, v, point(0, 1E5)), update2(p, v, point(1E5, 0));
	}
	solve();
}

@details@

注意一下凸包上可能会有重合 / 共线的点，都要排除掉。

求凸包之间涉及到求两个凸多边形的交（对应不能跑出界限），看上去要半平面交，实际上把所有可能的点求出来暴力判是否在两个多边形内就可以了。