机器学习5- 对数几率回归+Python实现

1. 对数几率回归
- 1.1 求解 ω 和 b
2. 对数几率回归进行垃圾邮件分类
- 2.1 垃圾邮件分类
- 2.2 模型评估

1. 对数几率回归

考虑二分类任务，其输出标记 \(y \in \{0, 1\}\)，记线性回归模型产生的预测值 \(z=\boldsymbol{w}^T\boldsymbol{x} + b\) 是实值，于是我们需要一个将实值 \(z\) 转换为 \(0/1\) 的 \(g^{-}(\cdot)\)。

最理想的单位阶跃函数（unit-step function）

\[y = \begin{cases}
0, & z < 0 \\
0.5, & z = 0 \\
1, & z > 0 \\
\end{cases}
\tag{1.1}
\]

并不是连续函数，因此不能作为 \(g^-(\cdot)\) 。于是我们选用对数几率函数（logistics function）作为单位阶跃函数的替代函数（surrogate function）：

\[y = \frac{1}{1+e^{-z}} \tag{1.2}
\]

如下图所示：

对数几率函数是 Sigmoid 函数（即形似 S 的函数）的一种。

将对数几率函数作为 \(g^-(\cdot)\) 得到

\[y = \frac{1}{1+e^{-(\boldsymbol{w}^T\boldsymbol{x} + b)}} \tag{1.3}
\]

\[\ln \frac{y}{1-y} = \boldsymbol{w}^T\boldsymbol{x} + b \tag{1.4}
\]

若将 \(y\) 视为样本 \(\boldsymbol{x}\) 为正例的可能性，则 \(1-y\) 是其为反例的可能性，两者的比值为

\[\frac{y}{1-y} \tag{1.5}
\]

称为几率（odds），反映了 \(\boldsymbol{x}\) 作为正例的相对可能性。对几率取对数得到对数几率（log odds，或 logit）：

\[\ln \frac{y}{1-y} \tag{1.6}
\]

所以，式 (1.3) 实际上是用线性回归模型的预测结果取逼近真实标记的对数几率，因此其对应的模型又称为对数几率回归（logistic regression，或 logit regression）。

这种分类学习方法直接对分类可能性进行建模，无需事先假设数据分布，避免了假设分布不准确带来的问题；

它能得到近似概率预测，这对需要利用概率辅助决策的任务很有用；

对率函数是任意阶可导的凸函数，有很好的数学性质，许多数值优化算法都可直接用于求解最优解。

1.1 求解 ω 和 b

将式 (1.3) 中的 \(y\) 视为类后验概率估计 \(p(y = 1 | \boldsymbol{x})\)，则式 (1.4) 可重写为

\[\ln \frac{p(y=1 | \boldsymbol{x})}{p(y=0 | \boldsymbol{x})} = \boldsymbol{w}^T\boldsymbol{x} + b \tag{1.7}
\]

有

\[p(y=1|\boldsymbol{x}) = \frac{e^{\boldsymbol{w}^T\boldsymbol{x} + b}}{1+e^{\boldsymbol{w}^T\boldsymbol{x} + b}} \tag{1.8}
\]

\[p(y=0|\boldsymbol{x}) = \frac{1}{1+e^{\boldsymbol{w}^T\boldsymbol{x} + b}} \tag{1.9}
\]

通过极大似然法（maximum likelihood method）来估计 \(\boldsymbol{w}\) 和 \(b\) 。

给定数据集 \(\{(\boldsymbol{x}_i, y_i)\}^m_{i=1}\)，对率回归模型最大化对数似然（log-likelihood）:

\[\ell(\boldsymbol{w},b)=\sum\limits_{i=1}^m \ln p(y_i|\boldsymbol{x}_i;\boldsymbol{w},b) \tag{1.10}
\]

即令每个样本属于其真实标记的概率越大越好。

令 \(\boldsymbol{\beta} = (\boldsymbol{w};b)\)，\(\hat{\boldsymbol{x}} = (\boldsymbol{x};1)\)，则 \(\boldsymbol{w}^T\boldsymbol{x} + b\) 可简写为 \(\boldsymbol{\beta}^T\hat{\boldsymbol{x}}\)。再令 \(p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta}) = p(y=1|\hat{\boldsymbol{x}};\boldsymbol{\beta})\)，\(p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta}) = p(y=0|\hat{\boldsymbol{x}};\boldsymbol{\beta}) = 1-p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta})\) 。则式 (1.10) 可简写为：

\[p(y_i|\boldsymbol{x}_i;\boldsymbol{w},b) = y_ip_1(\hat{\boldsymbol{x}};\boldsymbol{\beta}) +(1-y_i)p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta}) \tag{1.11}
\]

将式 (1.11) 带入 (1.10)，并根据式 (1.8) 和 (1.9) 可知，最大化式 (1.10) 等价于最小化

\[\ell(\boldsymbol{\beta}) = \sum\limits_{i=1}^m\Big(-y_i\boldsymbol{\beta}^T\hat{\boldsymbol{x}}_i+\ln\big(1+e^{\boldsymbol{\beta}^T+\hat{\boldsymbol{x}}_i}\big)\Big) \tag{1.12}
\]

式 (1.12) 是关于 \(\boldsymbol{\beta}\) 的高阶可导凸函数，根据凸优化理论，经典的数值优化算法如梯度下降法（gradient descent method）、牛顿法（Newton method）等都可求得其最优解，于是得到：

\[\boldsymbol{\beta}^{*} = \underset{\boldsymbol{\beta}}{\text{arg min }}\ell(\boldsymbol{\beta}) \tag{1.13}
\]

以牛顿法为例，其第 \(t+1\) 轮迭代解的更新公式为：

\[\boldsymbol{\beta}^{t+1} = \boldsymbol{\beta}^t-\Big(\frac{\partial^2\ell(\boldsymbol{\beta})}{\partial\boldsymbol{\beta}\ \partial\boldsymbol{\beta}^T}\Big)^{-1}\frac{\partial\ell(\boldsymbol{\beta})}{\partial{\boldsymbol{\beta}}} \tag{1.14}
\]

其中关于 \(\boldsymbol{\beta}\) 的一阶、二阶导数分别为：

\[\frac{\partial\ell(\boldsymbol{\beta})}{\partial\boldsymbol{\beta}} = -\sum\limits_{i=1}^m\hat{\boldsymbol{x}}_i(y_i-p_1(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta})) \tag{1.15}
\]

\[\frac{\partial^2{\ell(\boldsymbol{\beta})}}{\partial\boldsymbol{\beta}\partial\boldsymbol{\beta}^T} = \sum\limits_{i=1}^m\hat{\boldsymbol{x}}_i\hat{\boldsymbol{x}}_i^Tp_1(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta})(1-p_1(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta})) \tag{1.16}
\]

2. 对数几率回归进行垃圾邮件分类

2.1 垃圾邮件分类

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from sklearn.linear_model.logistic import LogisticRegression

from sklearn.model_selection import train_test_split, cross_val_score

from sklearn.feature_extraction.text import TfidfVectorizer

from matplotlib.font_manager import FontProperties

df = pd.read_csv("SMSSpamCollection", delimiter='\t', header=None)

df.head()

print("spam 数量: ", df[df[0] == 'spam'][0].count())

print("ham 数量: ", df[df[0] == 'ham'][0].count())

spam 数量:  747

ham 数量:  4825

X_train_raw, X_test_raw, y_train, y_test = train_test_split(df[1], df[0])

# 计算TF-IDF权重

vectorizer = TfidfVectorizer()

X_train = vectorizer.fit_transform(X_train_raw)

X_test = vectorizer.transform(X_test_raw)

# 建立模型

classifier = LogisticRegression()

classifier.fit(X_train, y_train)

y_preds = classifier.predict(X_test)

for i, y_pred in enumerate(y_preds[-10:]):

    print("预测类型: %s -- 信息: %s" % (y_pred, X_test_raw.iloc[i]))

预测类型: ham -- 信息: Aight no rush, I'll ask jay

预测类型: ham -- 信息: Sos! Any amount i can get pls.

预测类型: ham -- 信息: You unbelievable faglord

预测类型: ham -- 信息: Carlos'll be here in a minute if you still need to buy

预测类型: spam -- 信息: Meet after lunch la...

预测类型: ham -- 信息: Hey tmr maybe can meet you at yck

预测类型: ham -- 信息: I'm on da bus going home...

预测类型: ham -- 信息: O was not into fps then.

预测类型: ham -- 信息: Yes..he is really great..bhaji told kallis best cricketer after sachin in world:).very tough to get out.

预测类型: ham -- 信息: Did you show him and wot did he say or could u not c him 4 dust?

2.2 模型评估

混淆举证

test = y_test

test[test == "ham"] = 0

test[test == "spam"] = 1

pred = y_preds

pred[pred == "ham"] = 0

pred[pred == "spam"] = 1

from sklearn.metrics import confusion_matrix

test = test.astype('int')

pred = pred.astype('int')

confusion_matrix = confusion_matrix(test.values, pred)

print(confusion_matrix)

plt.matshow(confusion_matrix)

font = FontProperties(fname=r"/usr/share/fonts/opentype/noto/NotoSansCJK-Regular.ttc")

plt.title(' 混淆矩阵',fontproperties=font)

plt.colorbar()

plt.ylabel(' 实际类型',fontproperties=font)

plt.xlabel(' 预测类型',fontproperties=font)

plt.show()

[[1191    1]

 [  50  151]]

精度

from sklearn.metrics import accuracy_score

print(accuracy_score(test.values, pred))

0.9633883704235463

交叉验证精度

df = pd.read_csv("sms.csv")

df.head()

X_train_raw, X_test_raw, y_train, y_test = train_test_split(df['message'], df['label'])

vectorizer = TfidfVectorizer()

X_train = vectorizer.fit_transform(X_train_raw)

X_test = vectorizer.transform(X_test_raw)

classifier = LogisticRegression()

classifier.fit(X_train, y_train)

scores = cross_val_score(classifier, X_train, y_train, cv=5)

print(' 精度:',np.mean(scores), scores)

 精度: 0.9562200956937799 [0.94736842 0.95933014 0.95574163 0.95574163 0.96291866]

准确率召回率

precisions = cross_val_score(classifier, X_train, y_train, cv=5, scoring='precision')

print('准确率:', np.mean(precisions), precisions)

recalls = cross_val_score(classifier, X_train, y_train, cv=5, scoring='recall')

print('召回率:', np.mean(recalls), recalls)

准确率: 0.9920944081237428 [0.98550725 1.         1.         0.98701299 0.98795181]

召回率: 0.6778796653796653 [0.61261261 0.69642857 0.66964286 0.67857143 0.73214286]

F1 度量

f1s = cross_val_score(classifier, X_train, y_train, cv=5, scoring='f1')

print(' 综合评价指标:', np.mean(f1s), f1s)

 综合评价指标: 0.8048011339652206 [0.75555556 0.82105263 0.80213904 0.8042328  0.84102564]

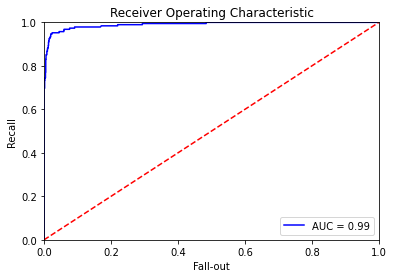
ROC AUC

from sklearn.metrics import roc_curve, auc

predictions = classifier.predict_proba(X_test)

false_positive_rate, recall, thresholds = roc_curve(y_test, predictions[:, 1])

roc_auc = auc(false_positive_rate, recall)

plt.title('Receiver Operating Characteristic')

plt.plot(false_positive_rate, recall, 'b', label='AUC = %0.2f' % roc_auc)

plt.legend(loc='lower right')

plt.plot([0, 1], [0, 1], 'r--')

plt.xlim([0.0, 1.0])

plt.ylim([0.0, 1.0])

plt.ylabel('Recall')

plt.xlabel('Fall-out')

plt.show()