Java实现第八届蓝桥杯魔方状态

魔方状态

题目描述

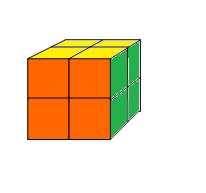
二阶魔方就是只有2层的魔方，只由8个小块组成。

如图p1.png所示。

小明很淘气，他只喜欢3种颜色，所有把家里的二阶魔方重新涂了颜色，如下：

前面：橙色

右面：绿色

上面：黄色

左面：绿色

下面：橙色

后面：黄色

请你计算一下，这样的魔方被打乱后，一共有多少种不同的状态。

如果两个状态经过魔方的整体旋转后，各个面的颜色都一致，则认为是同一状态。

请提交表示状态数的整数，不要填写任何多余内容或说明文字。

开始拿到这道题没什么思路，笔算算不来，模拟判重感觉太麻烦。大神说burnside引理可以做，学渣表示看不懂。。网上基本没有求解的，有的也答案不一。最后还是模拟判重这么写了。

我的答案：229878

测试：全同色魔方状态为1，正确。正常二阶魔方状态3674160，正确。

思路：其实就是空间状态搜索。模拟操作+判重。关于操作，二阶魔方只做U(顶层顺时针) R(右层顺时针) F(前层顺时针)就可以得到所有状态了。判重需要旋转整个魔方去比较。（判重小白现在只会用set）。

然后是，怎么去表示一个二阶魔方。二阶魔方8个块，一个块6面(看不见的作黑色考虑)，所以我用了char st[8][7]去表示一个魔方。块的顺序如下：

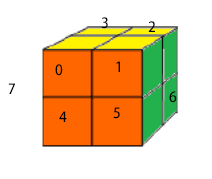
上面的初始状态表示就是{{“oybbgb”},{“oygbbb”},{“bygbby”},{“bybbgy”},{“obbogb”},{“obgobb”},{“bbgoby”},{“bbbogy”}}

o表示橙色，b表示黑色，g表示绿色，y表示黄色。

对于一个小块，6个面的颜色定义顺序如下：

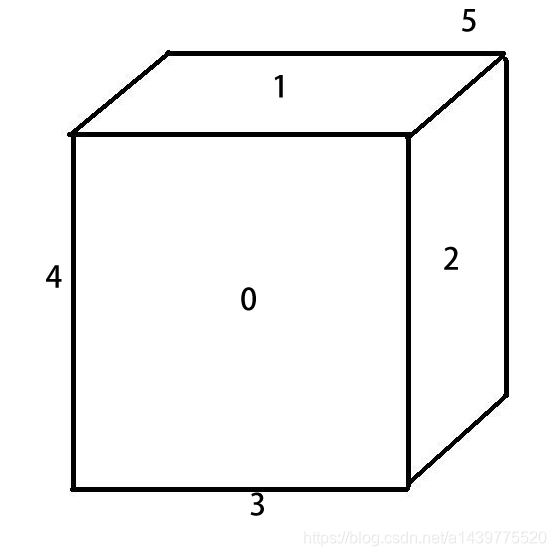
所以，比如说，上面题目给的魔方，前面一层，左上角的橙黄绿块，表示就是oybbgb

博主还是个小白，只能找来C++的代码，还望 Java大佬及时写出

#include <bits/stdc++.h>
using namespace std;
typedef char st[8][7];
st state[2000000];
set<string> all;
st begin={{"oybbgb"},{"oygbbb"},{"bygbby"},{"bybbgy"},{"obbogb"},{"obgobb"},{"bbgoby"},{"bbbogy"}};
//st begin={{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"},{"oooooo"}};
//只有一个颜色的魔方 ans=1
//st begin={{"rykkbk"},{"rygkkk"},{"kygkko"},{"kykkbo"},{"rkkwbk"},{"rkgwkk"},{"kkgwko"},{"kkkwbo"}};
//正常2阶魔方状态  r红 y黄 b蓝 g绿 w白 o橙  k黑(红对橙，白对黄，蓝对绿，颜色相近的相对)这里白为底 前为红
//需要将state大小改为4000000
//这个测试用例跑了20分钟左右 560M内存  ans=3674160 与实际二阶魔方状态数相同 见下截图
int front, tail;
void ucell(char *a){swap(a[0], a[2]); swap(a[2], a[5]); swap(a[5], a[4]);}
void rcell(char *a){swap(a[1], a[0]); swap(a[0], a[3]); swap(a[3], a[5]);}
void fcell(char *a){swap(a[2], a[1]); swap(a[1], a[4]); swap(a[4], a[3]);}
void u(st &s)//顶层顺时针旋转
{
	ucell(s[0]);
	ucell(s[1]);
	ucell(s[2]);
	ucell(s[3]);
	swap(s[1], s[0]);
	swap(s[2], s[1]);
	swap(s[3], s[2]);
}
void uwhole(st &s)//整个魔方从顶部看 顺时针转 用于判重
{
	u(s);
	ucell(s[4]);
	ucell(s[5]);
	ucell(s[6]);
	ucell(s[7]);
	swap(s[5], s[4]);
	swap(s[6], s[5]);
	swap(s[7], s[6]);
}
void f(st &s)//前面一层 顺时针转
{
	fcell(s[0]);
	fcell(s[1]);
	fcell(s[4]);
	fcell(s[5]);
	swap(s[1], s[5]);
	swap(s[0], s[1]);
	swap(s[4], s[0]);
}
void fwhole(st &s)//整个魔方从前面看 顺时针转 用于判重
{
	f(s);
	fcell(s[2]);
	fcell(s[6]);
	fcell(s[7]);
	fcell(s[3]);
	swap(s[2], s[6]);
	swap(s[3], s[2]);
	swap(s[7], s[3]);
}
void r(st &s)//魔方右层顺时针转
{
	rcell(s[1]);
	rcell(s[2]);
	rcell(s[6]);
	rcell(s[5]);
	swap(s[2], s[1]);
	swap(s[5], s[1]);
	swap(s[6], s[5]);
}
void rwhole(st &s)//整个魔方从右边看 顺时针转 用于判重
{
	r(s);
	rcell(s[0]);
	rcell(s[3]);
	rcell(s[4]);
	rcell(s[7]);
	swap(s[3], s[7]);
	swap(s[0], s[3]);
	swap(s[4], s[0]);
}
string convert(st &s)//魔方状态二维字符数组 转化为string
{
	string ss;
	for(int i=0; i<8; i++)ss+=s[i];
	return ss;
}
bool try_to_insert(int tail)//判重
{
	st k;
	memcpy((void*)k, (void*)state[tail], sizeof(state[tail]));
	for(int i=0; i<4; i++)
	{
		fwhole(k);
		for(int j=0; j<4; j++)
		{
			uwhole(k);
			for(int q=0; q<4; q++)
			{
				rwhole(k);
				if(all.count(convert(k))==1)
				{
					return false;
				}
			}
		}
	}
	all.insert(convert(k));
	return true;
}
int main()
{
	front=0,tail=1;
	all.insert(convert(begin));
	memcpy((void*)state[0],(void*)begin,sizeof(begin));
	while(front!=tail)
	{
		//对当前状态分别模拟三种操作U R F 然后判重
		for(int i=0; i<3; i++)
		{
			memcpy((void*)state[tail], (void*)state[front], sizeof(state[front]));
			if(i==0)
			{
				u(state[tail]);
				if(try_to_insert(tail))tail++;
			}
			else if(i==1)
			{
				r(state[tail]);
				if(try_to_insert(tail))tail++;
			}
			else if(i==2)
			{
				f(state[tail]);
				if(try_to_insert(tail))tail++;
			}
		}
		front++;
	}
	cout<<front<<endl;
	return 0;
}
//ans 229878