HDU 1558 Segment set（ 判断线段相交 + 并查集 ）

---

**链接：****传送门 **

题意：输入一个数 n 代表有 n 组操作，P 是在平面内加入一条线段，Q x 是查询第 x 条线段所在相交集合的线段个数

• 例如：下图 5 与 1、2 相交，1 与 3 相交，2 与 4 相交，所以这个相交集合的线段为 1、2、3、4、5，所以 Q 5 答案为 5
  
  

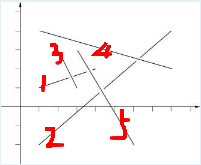
思路：

1. 可以使用并查积来描述“相交集合”，如果两个线段相交，就 unite 这两个线段所在集合，需要注意的是，在进行 unite 的时候，需要对两个集合中所有元素进行处理

2. 如何查询每个集合中线段的个数？题目给的数据量较小，可以直接扫描整个 par[] 数组来记录个数

balabala：下面两种做法再次体现了知识面的决定性作用TAT！方法1——46 Ms AC ，方法2——156 Ms AC！接近4倍的时间！

---

方法1：加一个数组维护集合中线段的个数，这个想法来源于这一道题 ---> 戳这里！

/*************************************************************************
    > File Name: hdu1558t2.cpp
    > Author:    WArobot
    > Blog:      http://www.cnblogs.com/WArobot/
    > Created Time: 2017年05月08日 星期一 19时38分36秒
 ************************************************************************/

#include<bits/stdc++.h>
using namespace std;

#define eps 1e-10
const int maxn = 1010;
struct point{ double x,y; };
struct V{ point s,e; };
int par[maxn] , num[maxn];	

// 线段相交部分
bool inter(point a,point b,point c,point d){
    if( min(a.x,b.x) > max(c.x,d.x) ||
	min(a.y,b.y) > max(c.y,d.y) ||
	min(c.x,d.x) > max(a.x,b.x) ||
	min(c.y,d.y) > max(a.y,b.y)
    )return 0;
    double h,i,j,k;
    h = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
    i = (b.x-a.x)*(d.y-a.y) - (b.y-a.y)*(d.x-a.x);
    j = (d.x-c.x)*(a.y-c.y) - (d.y-c.y)*(a.x-c.x);
    k = (d.x-c.x)*(b.y-c.y) - (d.y-c.y)*(b.x-c.x);
    return h*i<=eps && j*k<=eps;
}
// 并查集部分
void init(){
	for(int i=0;i<maxn;i++){
		par[i] = i;
		num[i] = 1;
	}
}
int find(int x){
	if(par[x] == x)	return x;
	else			return par[x] = find(par[x]);
}
void unite(int x,int y){
	x = find(x);
	y = find(y);
	if(x==y)	return;
	else{
		par[y] = x;
		num[x] += num[y];	// 在合并的同时维护集合数目
	}
}

void solve(int k,int x){
	int fx = find(x);
	unite( k , x );
	/*for(int i = 0 ; i < k ; i++){
		if( par[i] == fx )	par[i] = k;
	}*/
}
int main(){
	int T , N , x , k , kase = 0;;
	string op;
	V v[maxn];
	scanf("%d",&T);
	while(T--){
		if( kase > 0 )	printf("\n");
		kase++;

		init();		// 初始化并查集

		scanf("%d",&N);
		k = 0;
		while(N--){
			cin>>op;
			if( op == "P" ){
				scanf("%lf%lf%lf%lf", &v[k].s.x , &v[k].s.y , &v[k].e.x , &v[k].e.y );
				for(int i = 0 ; i < k ; i++){
					if( inter(v[k].s,v[k].e,v[i].s,v[i].e) )
						solve( k , i );
				}
				k++;
			}
			else{
				scanf("%d",&x);		x -= 1;
				/*int cnt = 0;
				for(int i = 0 ; i <= k ; i++){
					if( par[i] == par[x] ) cnt++;
				}
				printf("%d\n",cnt);*/
				printf("%d\n", num[ find(x) ] );
			}
		}
		/*for(int i = 0 ; i < k ; i++){
			printf("i = %d , par[i] = %d\n",i,par[i]);
		}*/
	}
	return 0;
}

---

方法2：非常非常蠢的写法

/*************************************************************************
    > File Name: hdu1558.cpp
    > Author:    WArobot
    > Blog:      http://www.cnblogs.com/WArobot/
    > Created Time: 2017年05月08日 星期一 00时00分36秒
 ************************************************************************/

#include<bits/stdc++.h>
using namespace std;

#define eps 1e-10
const int maxn = 1010;
struct point{ double x,y; };
struct V{ point s,e; };
int par[maxn];	

// 线段相交部分
bool inter(point a,point b,point c,point d){
    if( min(a.x,b.x) > max(c.x,d.x) ||
	min(a.y,b.y) > max(c.y,d.y) ||
	min(c.x,d.x) > max(a.x,b.x) ||
	min(c.y,d.y) > max(a.y,b.y)
    )return 0;
    double h,i,j,k;
    h = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
    i = (b.x-a.x)*(d.y-a.y) - (b.y-a.y)*(d.x-a.x);
    j = (d.x-c.x)*(a.y-c.y) - (d.y-c.y)*(a.x-c.x);
    k = (d.x-c.x)*(b.y-c.y) - (d.y-c.y)*(b.x-c.x);
    return h*i<=eps && j*k<=eps;
}
// 并查集部分
void init(){
	for(int i=0;i<maxn;i++){
		par[i] = i;
	}
}
int find(int x){
	if(par[x] == x)	return x;
	else			return par[x] = find(par[x]);
}
void unite(int x,int y){
	x = find(x);
	y = find(y);
	if(x==y)	return;
	else		par[y] = x;
}

void solve(int k,int x){
	int fx = find(x);	// 先找到 x 的祖先再合并 x，否则合并之后就无法处理原本 x 所在集合的所有元素了
	unite( k , x );
	for(int i = 0 ; i < k ; i++){
		if( par[i] == fx )	par[i] = k;
	}
}
int main(){
	int T , N , x , k , kase = 0;;
	string op;
	V v[maxn];
	scanf("%d",&T);
	while(T--){
		if( kase > 0 )	printf("\n");
		kase++;

		init();		// 初始化并查集

		scanf("%d",&N);
		k = 0;
		while(N--){
			cin>>op;
			if( op == "P" ){
				scanf("%lf%lf%lf%lf", &v[k].s.x , &v[k].s.y , &v[k].e.x , &v[k].e.y );
				for(int i = 0 ; i < k ; i++){
					if( inter(v[k].s,v[k].e,v[i].s,v[i].e) )
						solve( k , i );
				}
				k++;
			}
			else{
				scanf("%d",&x);		x -= 1;
				int cnt = 0;
				for(int i = 0 ; i <= k ; i++){
					if( par[i] == par[x] ) cnt++;
				}
				printf("%d\n",cnt);
			}
		}
		/*for(int i = 0 ; i < k ; i++){
			printf("i = %d , par[i] = %d\n",i,par[i]);
		}*/
	}
	return 0;
}