[Luogu1273] 有线电视网

题目描述

某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。

从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。

现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。

写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

输入输出格式

输入格式：

输入文件的第一行包含两个用空格隔开的整数N和M，其中2≤N≤3000，1≤M≤N-1，N为整个有线电视网的结点总数，M为用户终端的数量。

第一个转播站即树的根结点编号为1，其他的转播站编号为2到N-M，用户终端编号为N-M+1到N。

接下来的N-M行每行表示—个转播站的数据，第i+1行表示第i个转播站的数据，其格式如下：

K A1 C1 A2 C2 … Ak Ck

K表示该转播站下接K个结点(转播站或用户)，每个结点对应一对整数A与C，A表示结点编号，C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。

输出格式：

输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。

输入输出样例

输入样例#1：

输出样例#1：

说明

样例解释

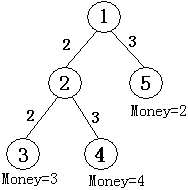
如图所示，共有五个结点。结点①为根结点，即现场直播站，②为一个中转站，③④⑤为用户端，共M个，编号从N-M+1到N，他们为观看比赛分别准备的钱数为3、4、2，从结点①可以传送信号到结点②，费用为2，也可以传送信号到结点⑤，费用为3（第二行数据所示），从结点②可以传输信号到结点③，费用为2。也可传输信号到结点④，费用为3（第三行数据所示），如果要让所有用户（③④⑤）都能看上比赛，则信号传输的总费用为：

2+3+2+3=10，大于用户愿意支付的总费用3+4+2=9，有线电视网就亏本了，而只让③④两个用户看比赛就不亏本了。

前两道都是什么乱七八糟的DP，来道树形DP，当然好像对我有点难

题解：

用f[i][j] 表示以i为根的子树选取j个用户的最小费用，

然后用树形DP常用的方法进行转移，最后从大到小找到第一个大于等于0的f[1][i]，i就是答案了

注意：转移的时候在将根的子树数量统计，不要一开始输入的时候就统计（当然这是我的方法）

所以其实这道题也不是很难吧

 %:pragma GCC optimize()

 #include<bits/stdc++.h>

 using namespace std;

 const int N=;

 vector <int> e[N];

 int f[N][N],s[N],c[N],fa[N],a[N],n,m;

 void dfs(int x,int fa){

     f[x][]=;

     for (int i=;i<e[x].size();++i) if (e[x][i]!=fa){

         int to=e[x][i]; dfs(to,x);

         for (int j=s[x];j>=;--j)

             for (int k=s[to];k>=;--k)

                 f[x][j+k]=max(f[x][j+k],f[x][j]+f[to][k]-c[to]);

         s[x]+=s[to];

     }

     if (e[x].size()==) f[x][]=a[x],s[x]=;

     return;

 }

 int main(){

     scanf("%d%d",&n,&m);

     memset(f,-0x3f3f,sizeof(f));

     for (int i=;i<=n-m;++i){

         int sum,x; scanf("%d",&sum);

         for (int j=;j<=sum;++j)

             scanf("%d",&x),scanf("%d",&c[x]),

             fa[x]=i,e[i].push_back(x);

     }

     for (int i=n-m+;i<=n;++i) scanf("%d",&a[i]);

     dfs(,);

     for (int i=m;i>=;--i)

         if (f[][i]>=){

             printf("%d",i); return ;

         }

 }