CodeForces 348C Subset Sums(分块)（nsqrtn）

C. Subset Sums

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a₁, a₂, ..., a_n and m sets S₁, S₂, ..., S_m of indices of elements of this array. Let's denote S_k = {S_k, i} (1 ≤ i ≤ |S_k|). In other words, S_k, i is some element from set S_k.

In this problem you have to answer q queries of the two types:

1. Find the sum of elements with indices from set S_k: 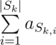. The query format is "? k".
2. Add number x to all elements at indices from set S_k: a_Sk, i is replaced by a_Sk, i + x for all i (1 ≤ i ≤ |S_k|). The query format is "+ k x".

After each first type query print the required sum.

Input

The first line contains integers n, m, q (1 ≤ n, m, q ≤ 10⁵). The second line contains n integers a₁, a₂, ..., a_n (|a_i| ≤ 10⁸) — elements of array a.

Each of the following m lines describes one set of indices. The k-th line first contains a positive integer, representing the number of elements in set (|S_k|), then follow |S_k| distinct integers S_k, 1, S_k, 2, ..., S_k, |Sk| (1 ≤ S_k, i ≤ n) — elements of set S_k.

The next q lines contain queries. Each query looks like either "? k" or "+ k x" and sits on a single line. For all queries the following limits are held: 1 ≤ k ≤ m, |x| ≤ 10⁸. The queries are given in order they need to be answered.

It is guaranteed that the sum of sizes of all sets S_k doesn't exceed 10⁵.

Output

After each first type query print the required sum on a single line.

Please, do not write the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

Examples

Input

5 3 5
5 -5 5 1 -4
2 1 2
4 2 1 4 5
2 2 5
? 2
+ 3 4
? 1
+ 2 1
? 2

Output

-3
4
9
【分析】一开始也想到了分块，但是一直以为是线段树，所以想歪了，然后看了网上的题解。。。太强了。

设B = sqrtn

先给集合分成两种， 一种是大小大于B的， 称为重集合， 小于的称为轻集合。

显然重集合的个数不会超过B个。

对每个集合， 求出它和每个重集合交集的大小， 即cnt[i][j]表示第i个集合和第j 个重集合交集的大小。 cnt数组可以O(NB)求出

对每个重集合， 维护add和sum， add表示加在这个集合上的值， sum表示这个集合没有加上其他重集合的附加值的和。

然后把操作分为4种：

1. 在轻集合上加值。 这样对每个轻集合里面的元素暴力加上v就行(O(B))。 同时要维护重集合的sum， 于是， 每个重集合的sum加上v*cnt[i][j]，(O(B))。复杂度(O(B))。

2. 在重集合上加值。 直接在重集合的add上加上v。 (O(1))

3. 询问轻集合。 ans 加上轻集合里面的元素的值， (O(B))。 然后再加上重集合的add[j] * cnt[i][j]， (O(B))。 O(B)

4. 询问重集合。 ans 加上重集合的sum， 然后再加上各个重集合的add[j] * cnt[i][j]。 O(B)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <stack>
#include <queue>
#include <vector>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
typedef long long ll;
using namespace std;
const int N = 1e5+;
const int M = ;
int n,m,q,k;
int cnt[][N],id[N],tot=;
int is[N];
ll a[N],add[N],sum[N];
vector<int>g[N],bl[N],big;
int main() {
    int u,v;
    scanf("%d%d%d",&n,&m,&q);
    int b=sqrt(n);
    for(int i=;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    for(int i=;i<=m;i++){
        scanf("%d",&k);
        if(k>b)id[i]=++tot,big.pb(id[i]),is[i]=;;
        for(int j=;j<k;j++){
            scanf("%d",&u);

            g[i].pb(u);
            if(k>b)bl[u].pb(tot),sum[tot]+=a[u];;
        }
    }
    for(int i=;i<=m;i++){
        for(int j=;j<g[i].size();j++){
            int u=g[i][j];
            for(int p=;p<bl[u].size();p++){
                cnt[bl[u][p]][i]++;
            }
        }
    }
    char str[];
    while(q--){
        scanf("%s",str);
        if(str[]=='+'){
            scanf("%d%d",&u,&v);
            if(is[u]){
                add[id[u]]+=v;
            }
            else {
                for(int i=;i<g[u].size();i++){
                    int c=g[u][i];
                    a[c]+=v;
                }
                for(int i=;i<big.size();i++){
                    int c=big[i];
                    sum[c]+=v*cnt[c][u];
                }
            }
        }
        else {
            scanf("%d",&u);
            if(is[u]){
                ll ans=sum[id[u]];
                for(int i=;i<big.size();i++){
                    int c=big[i];
                    ans+=add[c]*cnt[c][u];
                }
                printf("%lld\n",ans);
            }
            else {
                ll ans=;
                for(int i=;i<g[u].size();i++){
                    ans+=a[g[u][i]];
                }
                for(int i=;i<big.size();i++){
                    int c=big[i];
                    ans+=add[c]*cnt[c][u];
                }
                printf("%lld\n",ans);
            }
        }
    }
    return ;
}