1、数据双向绑定

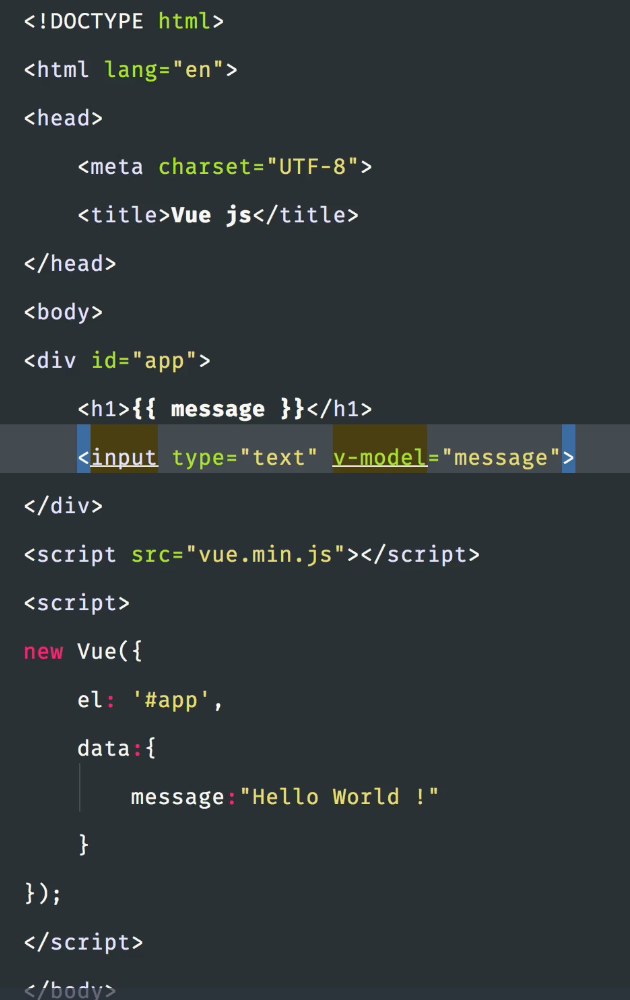
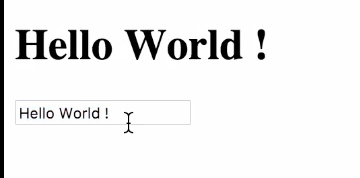
双向绑定以后，表单中数据的改变会同步改变H2中的输出

2、v-show

内容输入前：

内容输入后：隐藏提示，展示按钮

代码实现：

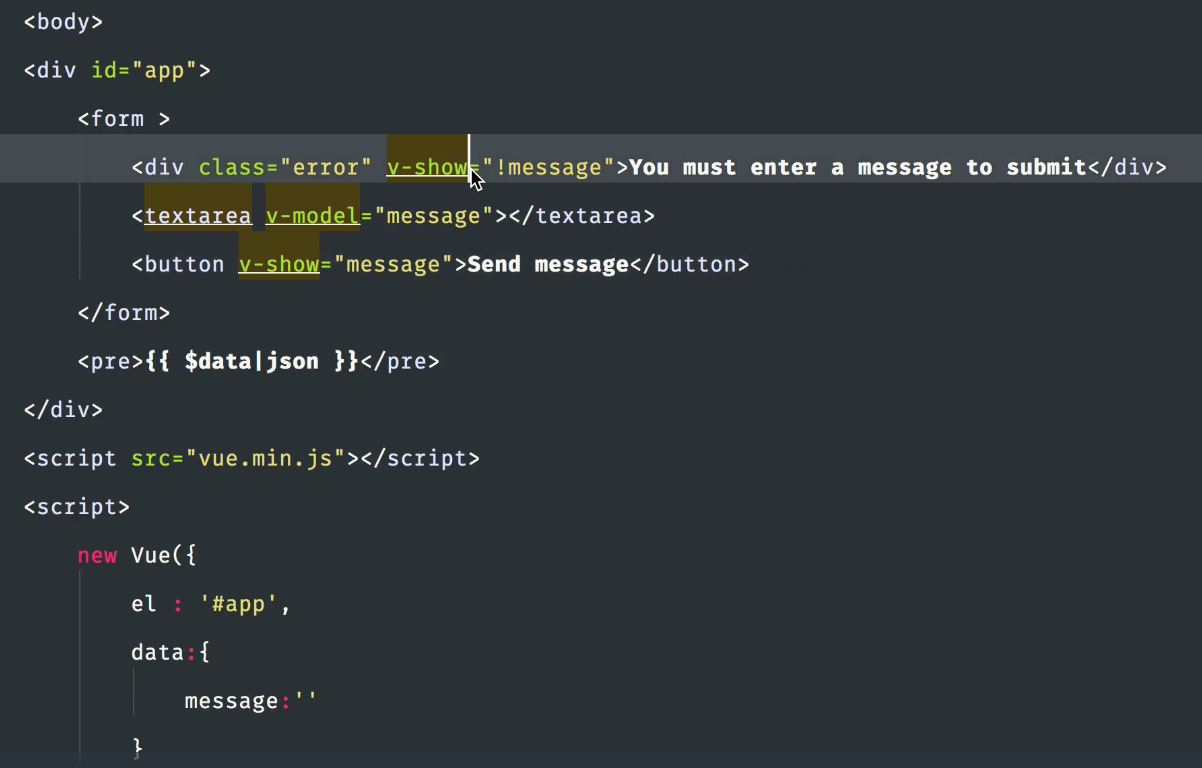
此处的v-show可以换成v-if，v-show是隐藏节点，v-if是删除节点

3、事件处理

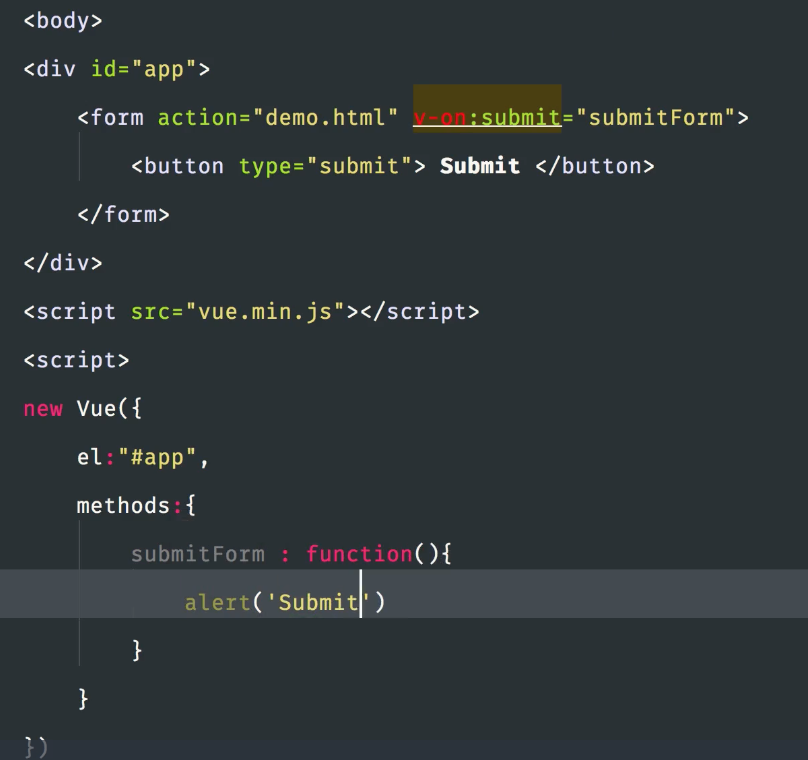
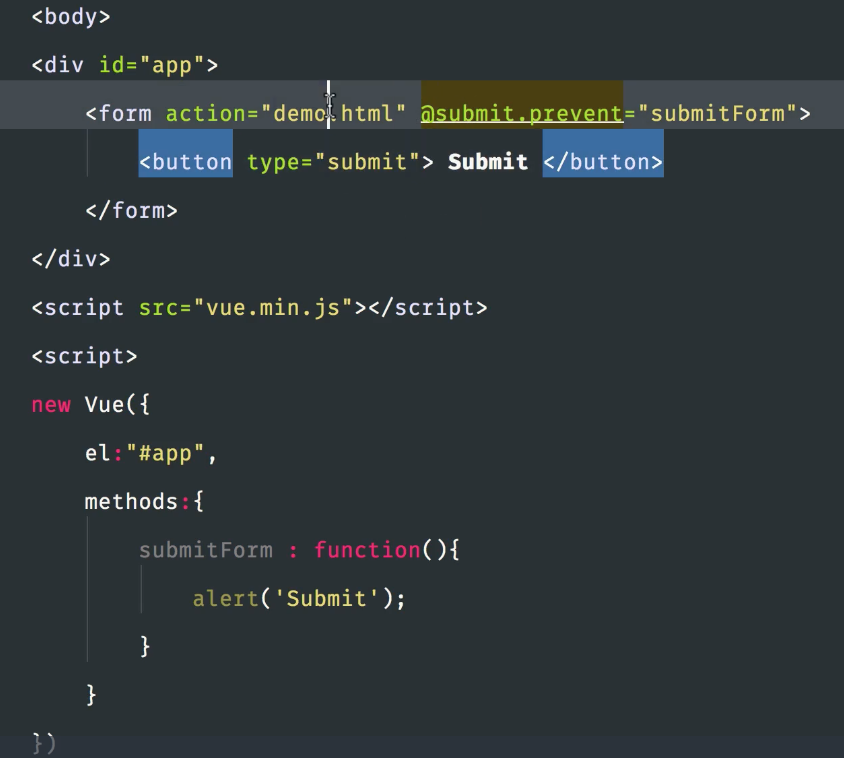
也可以阻止事件的执行，为了书写方便@替代了v-on：

点击提交后会执行sumitForm方法，但是不能执行submit方法了

click事件，点击+1

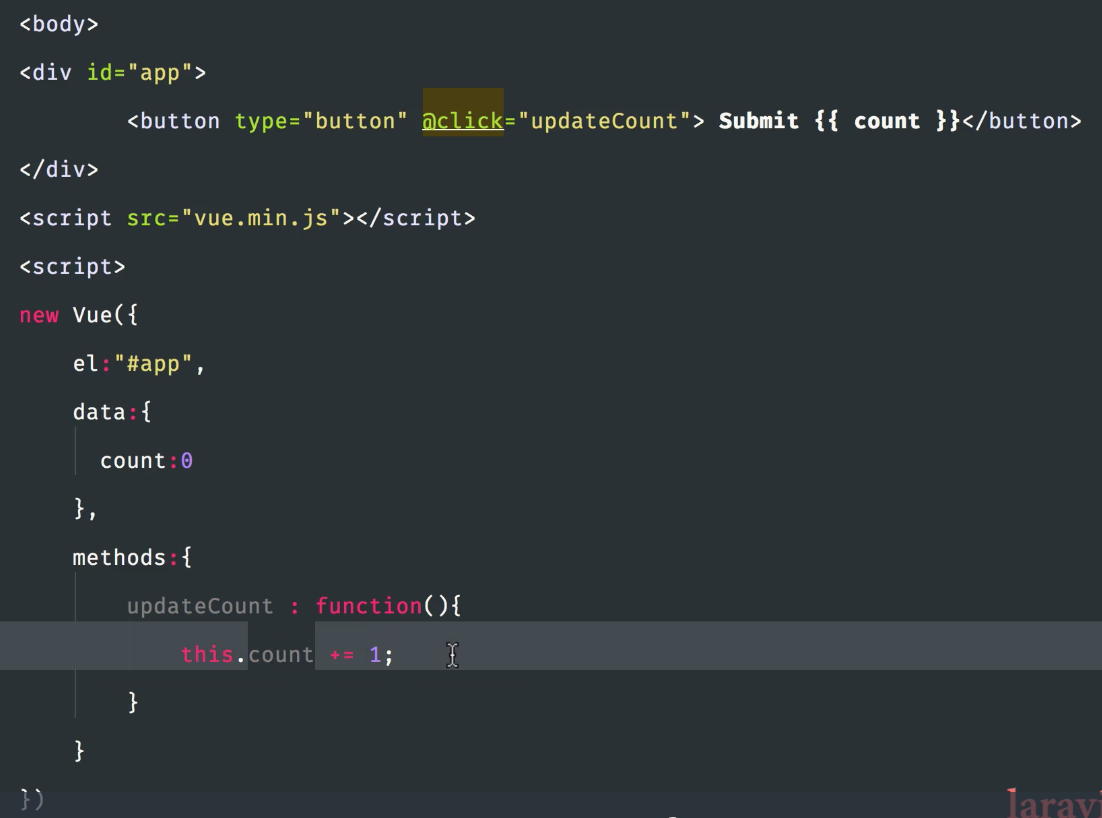
4、组件式开发

自定义标签、vue将内容填充进去

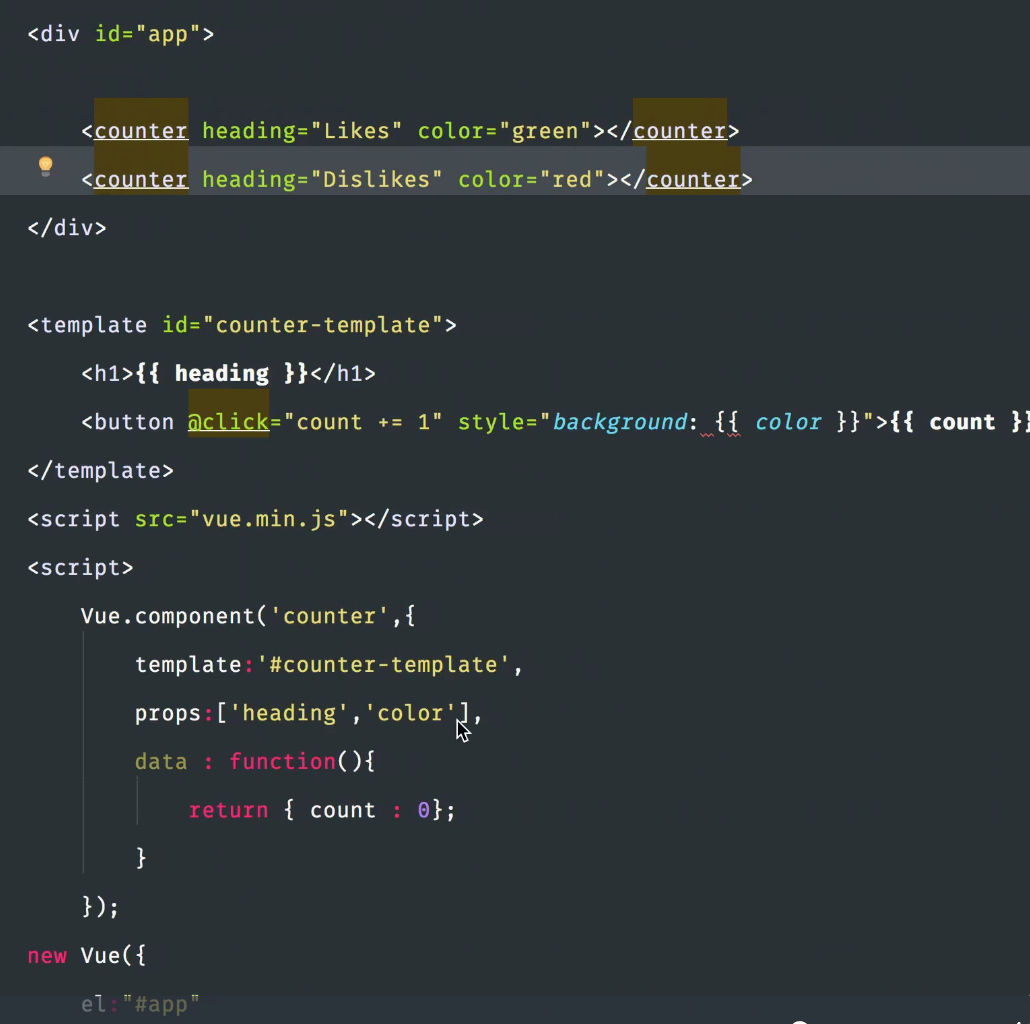
效果展示：

5、 两个彩蛋

5.1、引用cdn在线的未压缩JS，console会显示报错信息

5.2、谷歌插件——vue-devtools,方便调试

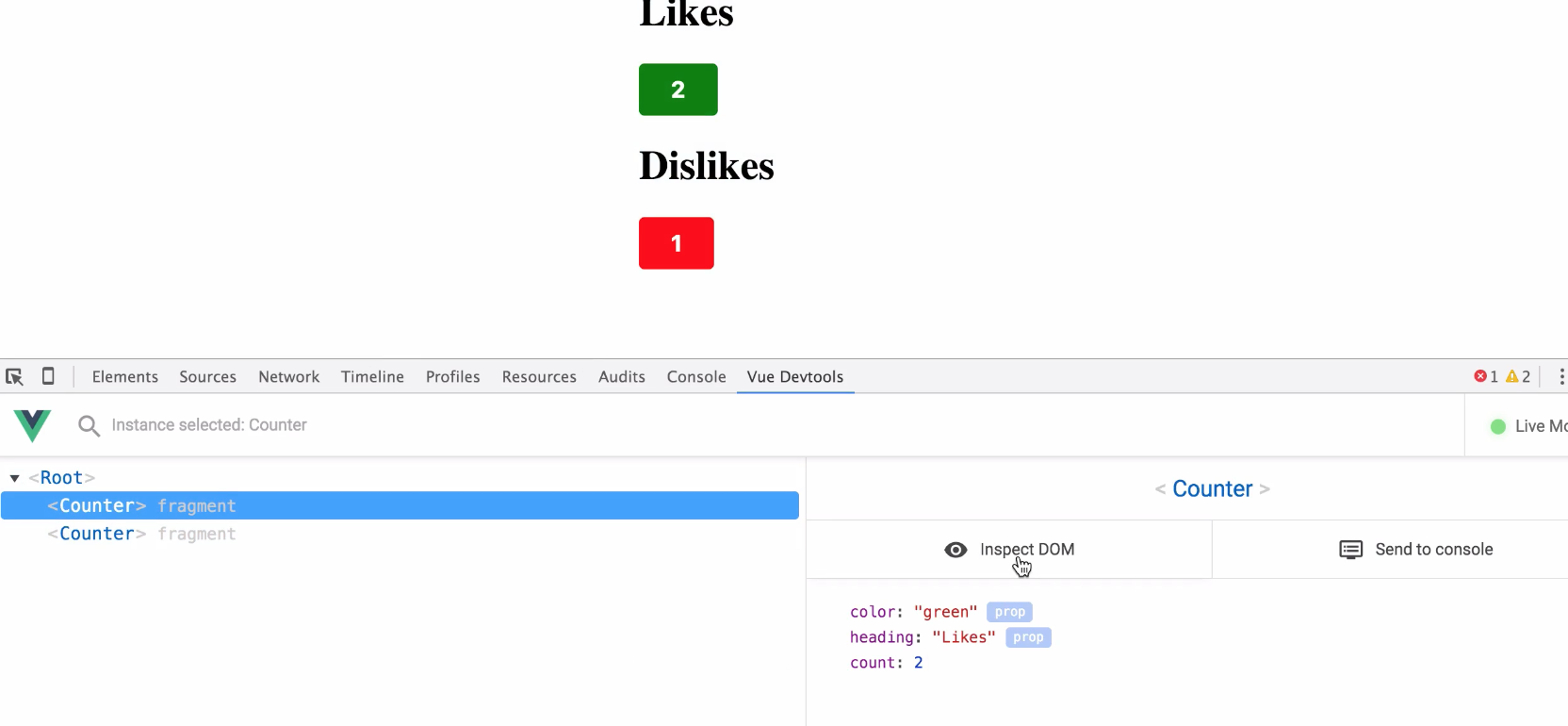
6、computed

computed property(计算过的属性) 一般用在处理一些逻辑复杂的数据输出

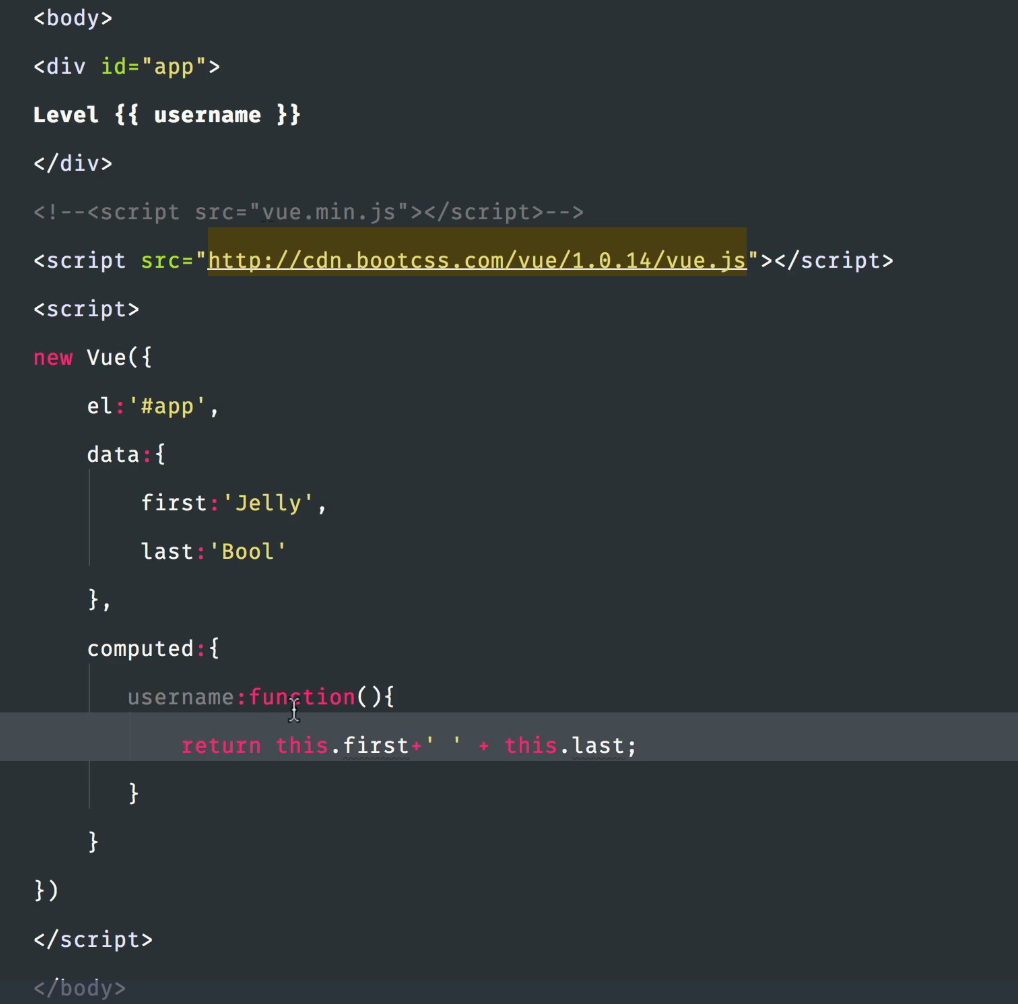
这样便会输出全名

7、列表显示

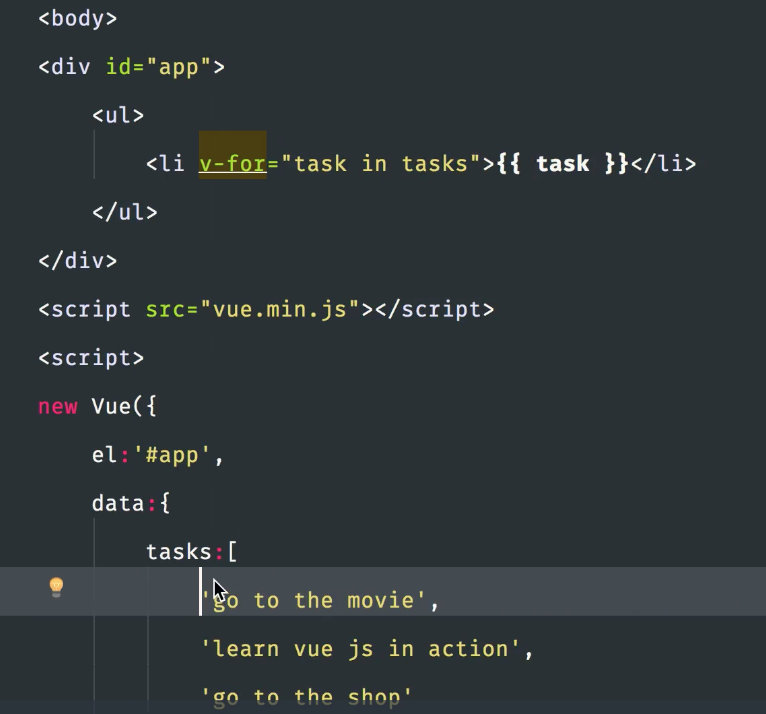
Vuejs1.0学习的更多相关文章

  1. Servlet3.0学习总结——基于Servlet3.0的文件上传

    Servlet3.0学习总结(三)——基于Servlet3.0的文件上传 在Servlet2.5中,我们要实现文件上传功能时,一般都需要借助第三方开源组件,例如Apache的commons-fileu ...

  2. solr6.0学习

    solr6.0学习(一)环境搭建准备工作:目前最新版本6.0.下载solr 6.0:Solr6.0下载JDK8 下载jdk1.8:jdk1.8[solr6.0是基于jdk8开发的]tomcat8.0 ...

  3. DirectX 总结和DirectX 9.0 学习笔记

    转自:http://www.cnblogs.com/graphics/archive/2009/11/25/1583682.html DirectX 总结 DDS DirectXDraw Surfac ...

  4. [EntLib]微软企业库5.0 学习之路——第一步、基本入门

    话说在大学的时候帮老师做项目的时候就已经接触过企业库了但是当初一直没明白为什么要用这个,只觉得好麻烦啊,竟然有那么多的乱七八糟的配置(原来我不知道有配置工具可以进行配置,请原谅我的小白). 直到去年在 ...

  5. Bootstrap3.0学习14

    Bootstrap3.0学习第十四轮(分页.徽章)   前言 阅读之前您也可以到Bootstrap3.0入门学习系列导航中进行查看http://www.cnblogs.com/aehyok/p/340 ...

  6. Bootstrap3.0学习第八轮

    Bootstrap3.0学习第八轮(工具Class)   前言 阅读之前您也可以到Bootstrap3.0入门学习系列导航中进行查看http://www.cnblogs.com/aehyok/p/34 ...

  7. Bootstrap3.0学习第六轮(表单)

    Bootstrap3.0学习第六轮(表单) 前言 阅读之前您也可以到Bootstrap3.0入门学习系列导航中进行查看http://www.cnblogs.com/aehyok/p/3404867.h ...

  8. Bootstrap3.0学习第三轮(栅格系统案例)

    Bootstrap3.0学习第三轮(栅格系统案例) 前言 在前面的一篇文章当中http://www.cnblogs.com/aehyok/p/3400499.html主要学习了栅格系统的基本原理,以及 ...

  9. 一起学ASP.NET Core 2.0学习笔记(二): ef core2.0 及mysql provider 、Fluent API相关配置及迁移

    不得不说微软的技术迭代还是很快的,上了微软的船就得跟着她走下去,前文一起学ASP.NET Core 2.0学习笔记(一): CentOS下 .net core2 sdk nginx.superviso ...

随机推荐

  1. Python执行Linux系统命令的4种方法

    http://www.jb51.net/article/56490.htm (1) os.system 仅仅在一个子终端运行系统命令,而不能获取命令执行后的返回信息 复制代码代码如下: system( ...

  2. node和gulp实现前端工程自动化(附：gulp常用插件)

    /** * 1. LESS编译 压缩 合并 * 2. JS合并 压缩 混淆 * 3. img复制 * 4. html压缩 */ // 在gulpfile中先载入gulp包,因为这个包提供了一些APIv ...

  3. 【bzoj2007】[Noi2010]海拔 最小割+对偶图+最短路

    题目描述 YT市是一个规划良好的城市,城市被东西向和南北向的主干道划分为n×n个区域.简单起见,可以将YT市看作一个正方形,每一个区域也可看作一个正方形.从而,YT城市中包括(n+1)×(n+1)个交 ...

  4. poj 2965 The Pilots Brothers' refrigerator (dfs)

    The Pilots Brothers' refrigerator Time Limit: 1000MS   Memory Limit: 65536K Total Submissions: 17450 ...

  5. LeetCode -- 3SumCloset

    Question: Given an array S of n integers, find three integers in S such that the sum is closest to a ...

  6. [Leetcode] Swap nodes in pairs 成对交换结点

    Given a linked list, swap every two adjacent nodes and return its head. For example,Given1->2-> ...

  7. vector 基础2

    size  :返回有效元素个数 max_size  :返回 vector 支持的最大元素个数 resize  :改变有效元素的个数 capacity  :返回当前可使用的最大元素内存块数(即存储容量) ...

  8. 给DOM元素绑定click事件也有学问

    最简单的莫过于使用click方法: 1 <input id="btn" type="button" value="BUTTON" on ...

  9. [poj 3281]最大流+建图很巧妙

    题目链接:http://poj.org/problem?id=3281 看了kuangbin大佬的思路,还用着kuangbin板子orz   http://www.cnblogs.com/kuangb ...

  10. AngularJs学习——实现数据绑定的三种方式

    三种方式: 方式一:<h5>{{msg}}</h5>  此方式在页面刷新的时候会闪现{{}} 方式二:<h5 ng-bind="msg">< ...