leetcode 88 Merge Sorted Array 归并排序

归并排序：先将数组一分为二，将左边部分排序（同样将其一分为二），再将右边部分排序，最后逐层归并。（分治策略）（稳定排序）。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

先排序的时间复杂度为log(n)；

后归并的时间复杂度为n；

总的时间复杂度nlog(n)。

 

1)自顶向下归并排序的代码：需要一个和待排序数组相同的空间，故将arr[]拷贝一份给aux[]

//将arr[l...mid]和 arr[mid+1...r]两部分进行归并
template<typename T>
void merge(T arr[], int l, int mid,  int r){
    //需要一个临时的和arr同样大小的空间
    T aux[r-l+];
    for(int i=l;i<=r;i++)
        //将arr复制给aus,aus下标从0开始，而arr下标从l开始
        aux[i-l] = arr[i];
    //初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int i = l, j = mid+;
    for(int k=l;k<=r;k++){
        //逐步比较左部分的第i个元素和右部分的第j个元素的大小
        //首先判断下标i和j的合法性
        if(i>mid){
            //左边已经遍历完，但右边还有
            arr[k] = aux[j-l];
            j++
        }
        else if(j>r){
            //右边已经遍历完，将左边的元素给arr
            arr[k] = aux[i-l];
            i++;
        }
        else if(aux[i-l]<aux[j-l]){
            arr[k] = aux[i-l];
            i++;
        }
        else{
            arr[k] = aux[j-l];
            j++;
        }
    }
}

//递归使用归并排序，对arr[l...r]的范围进行排序
template<typename T>
void mergeSort(T arr[], int l, int r){
    if(l>=r)
        return;
    int mid = (l+r)/;
    mergeSort(arr, l, mid);
    mergeSort(arr, mid+,r);
    //优化：只有当 mid>mid+1 时才需要对左右两边进行排序
    //因为左边或右边本身是有序的，如果 mid<=mid+1 则不需要对其归并排序了
    if(arr[mid] > arr[mid+])
        merge(arr,l,mid,r);
}

当数组中的元素足够少时，可以将递归出口改为插入排序，虽然插入排序的时间复杂度是O(n),但是可以提高效率。

2)自底向上归并排序：

template<typename T>      //泛型
void mergeSortBU(T arr[], int n){
    //自底向上归并
    //对merge的元素个数进行遍历：1，2，4，8以此类推
    for(int sz= ; sz<=n ; sz+=sz ){
        for(int i=; i+sz<n; i+=sz+sz)
            //对arr[i...i+sz-1]和arr[i+sz...i+2*sz-1]进行归并
            merge(arr, i, i+sz-, min(i+sz+sz-, n-));
    }
}

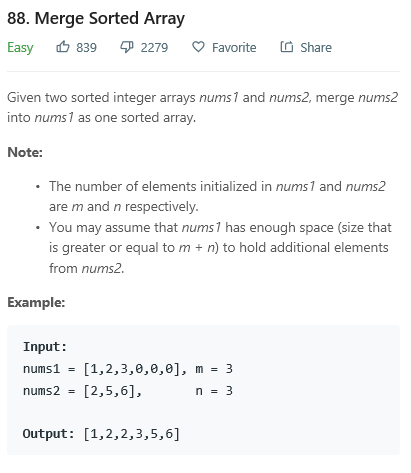
注意：nums1和nums2 是有序的，m代表nums1元素的个数。

这里的解题思想是归并排序的merge()函数的思想，先开辟一个与nums1相同大小和值的空间aux，再将其与nums2逐一对比，用小的来替换nums1的值。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {

        if (m <=  && n <= ) return;
        //int aux[m];
        vector<int> aux(m);
        for(int i=;i<m;i++){
            //将nums1的值拷贝给aux
            aux[i] = nums1[i];
        }

        int i=,j=;
        for(int k=;k<nums1.size();k++){
            if(i>m-){
                //aux数组超界
                nums1[k] = nums2[j];
                j++;
            }
            else if(j>n-){
                nums1[k] = aux[i];
                i++;
            }
            else if(nums2[j]<aux[i]){
                nums1[k] = nums2[j];
                j++;
            }
            else{
                nums1[k] = aux[i];
                i++;
            }

        }
    }
};

解法二：从两个数组的末尾开始比较大小，从下标为m+n-1开始存放，将大的存放在nums1的末尾。如果最后剩下的是nums1，则不需要移动；若是nums2中的元素则需要放在nums1的相应位置。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {

        if (m <=  && n <= ) return;

        int count = m+n-;
        --m, --n;   //m和n是长度，所以要减1变成下标
        while(m>= && n>=){
            if(nums1[m] >nums2[n])
                nums1[count--] = nums1[m--];
            else
                nums1[count--] = nums2[n--];
        }
        while(n>=){
           //当m已经全部遍历完，n还剩下
            nums1[count--] = nums2[n--];
        }
    }
};