poj 3177 Redundant Paths 求最少添加几条边成为双联通图： tarjan O(E)

 /**
 problem: http://poj.org/problem?id=3177
 tarjan blog: https://blog.csdn.net/reverie_mjp/article/details/51704523

 v 为下一结点， u为当前结点
 如果low[v] > dfn[u] 则 边(u,v)为桥
 缩点后剩下的所有边都为桥（缩点后即为树结构）
 将叶子结点相连使其成为双联通分量为最优解
 所以：
 添加(leaf + 1) / 2 条边即可使图成为双联通图
 **/
 #include<stdio.h>
 #include<stack>
 #include<algorithm>
 using namespace std;

 class Graphics{
     const static int MAXN = ;
     const static int MAXM =  * ;
 private:
     struct Edge{
         int to, next;
         bool bridge;
     }edge[MAXM];
     struct Point{
         int dfn, low, color;
     }point[MAXN];
     int first[MAXN], sign, sumOfPoint, dfnNum, colorNum;
     bool vis[MAXN];
     stack<int> stk;
     void tarjan(int u, int preEdge = -){
         point[u].low = dfnNum;
         point[u].dfn = dfnNum ++;
         vis[u] = true;
         stk.push(u);
         for(int i = first[u]; i != -; i = edge[i].next){
             int to = edge[i].to;
             if((i^) == preEdge) continue; /// 由于是双向边，防止由该边跑回原来的点
             if(!point[to].dfn){
                 tarjan(to, i);
                 point[u].low = min(point[u].low, point[to].low);
                 if(point[to].low > point[u].dfn){
                     edge[i].bridge = true;
                     edge[i^].bridge = true;
                 }
             }else if(vis[to]){
                 point[u].low = min(point[to].dfn, point[u].low);
             }
         }
         if(point[u].dfn == point[u].low){
             vis[u] = false;
             point[u].color = ++ colorNum;
             while(stk.top() != u){
                 point[stk.top()].color = colorNum;
                 vis[stk.top()] = false;
                 stk.pop();
             }
             stk.pop();
         }
     }
 public:
     void init(int n){
         sumOfPoint = n;
         for(int i = ; i <= n; i ++){
             first[i] = -;
             vis[i] = ;
         }
         sign = colorNum = ;
         dfnNum = ;
     }
     void addEdgeOneWay(int u, int v){
         edge[sign].to = v;
         edge[sign].next = first[u];
         edge[sign].bridge = false;
         first[u] = sign ++;
     }
     void addEdgeTwoWay(int u, int v){
         addEdgeOneWay(u, v);
         addEdgeOneWay(v, u);
     }
     void tarjanAllPoint(){
         for(int i = ; i <= sumOfPoint; i ++){
             if(!point[i].dfn)
                 tarjan(i);
         }
     }
     int getAns(){
         int *degree = new int[sumOfPoint+];
         int ans = ;
         for(int i = ; i <= sumOfPoint; i ++){
             degree[i] = ;
         }
         tarjanAllPoint();
         for(int i = ; i <= sumOfPoint; i ++){
             for(int j = first[i]; j != -; j = edge[j].next){
                 int to = edge[j].to;
                 if(edge[j].bridge){
                     degree[point[to].color] ++;
                 }
             }
         }
         for(int i = ; i <= sumOfPoint; i ++){
             if(degree[i] == ){
                 ans ++;
             }
         }
         delete []degree; return (ans + ) / ;
     }
 }graph;

 int main(){
     int f, r;
     scanf("%d%d", &f, &r);
     graph.init(f);
     while(r --){
         int a, b;
         scanf("%d%d", &a, &b);
         graph.addEdgeTwoWay(a, b);
     }
     printf("%d\n", graph.getAns());
     return ;
 }

ps:

防止由该边跑回原来的点不能判断（点）而要判断（边）即

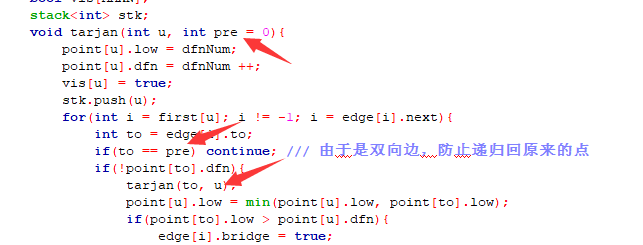
这么写是有bug的
例如：重边