图最短路径之Dijkstra

Dijkstra’s shortest path algorithm

算法参考地址：Dijsktra's algorithm (geeksforgeeks.org)

算法的简介：

1）该算法用来计算最短距离，但不计算路径信息。我们可以创建一个父数组，在距离更新时更新父数组如[prim的实现，并使用它来显示从源到不同顶点的最短路径。 2）代码用于无向图，相同的Dijkstra函数也可以用于有向图。 3） 代码查找从源到所有顶点的最短距离。如果我们只对从源到单个目标的最短距离感兴趣，我们可以在选取的最小距离顶点等于目标时中断for循环（算法的步骤3.a）。 4） 实现的时间复杂度为 O（V^2）。如果输入，则可以借助二进制堆将其简化为 O（E log V）。 5）Dijkstra的算法不适用于具有负权重周期的图形。对于具有负边的图形，可以使用Floyd或者Bellman-Ford算法。

算法的过程

给定图形和图形中的源顶点，查找从源到给定图形中所有顶点的最短路径。 Dijkstra的算法与[Prim的最小生成树算法]非常相似。与Prim的MST一样，我们生成一个SPT（最短路径树），以给定的源作为根。我们维护两个集合，一个集合包含最短路径树中包含的顶点，另一个集合包含尚未包含在最短路径树中的顶点。在算法的每一步中，我们都会找到一个位于另一个集合（尚未包含的集合）中的顶点，并且与源的距离最小。 以下是Dijkstra算法中使用的详细步骤，用于查找从单个源顶点到给定图中所有其他顶点的最短路径。

算法 1） 创建一个集合 sptSet（最短路径树集），用于跟踪最短路径树中包含的顶点，即计算并最终确定其与源的最小距离。最初，此集为空。 2） 为输入图中的所有顶点分配距离值。将所有距离值初始化为 INFINITE。为源顶点指定距离值为 0，以便首先选取它。 3） 虽然 sptSet 不包括所有顶点 ....a） 选择一个在 sptSet 中不存在且具有最小距离值的顶点 u。 ....b） 将您包括在 sptSet 中。 ....c） 更新您所有相邻顶点的距离值。要更新距离值，请循环访问所有相邻顶点。对于每个相邻顶点 v，如果 u 的距离值（来自源）和边 u-v 的权重之和小于 v 的距离值，则更新 v 的距离值。

让我们通过以下示例来理解：

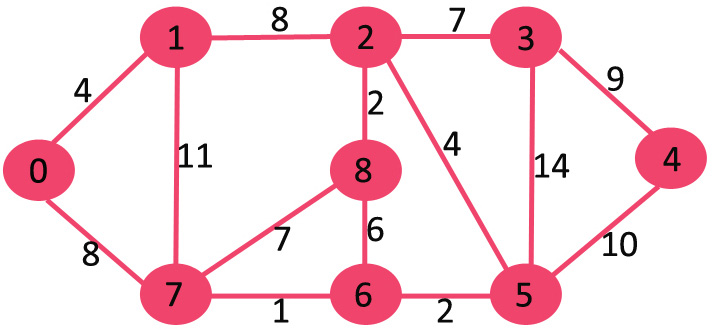
设置的 sptSet 最初是空的，分配给顶点的距离是 {0， INF， INF， INF， INF， INF， INF} ，其中 INF 表示无限。现在选取具有最小距离值的顶点。选取顶点 0，将其包含在 sptSet 中。所以sptSet变得{0}。在 sptSet 中包含 0 后，更新其相邻顶点的距离值。相邻顶点 0 为 1 和 7。距离值 1 和 7 将更新为 4 和 8。以下子图显示顶点及其距离值，仅显示具有有限距离值的顶点。SPT 中包含的顶点以绿色显示。

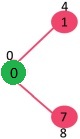
选取具有最小距离值且尚未包含在 SPT（不在 sptSET 中）的顶点。选取顶点 1 并将其添加到 sptSet 中。所以 sptSet 现在变成 {0， 1}。更新相邻顶点 1 的距离值。顶点 2 的距离值变为 12。

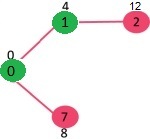
选取具有最小距离值且尚未包含在 SPT（不在 sptSET 中）的顶点。选取顶点 7。所以 sptSet 现在变成 {0， 1， 7}。更新相邻顶点的距离值 7。顶点 6 和 8 的距离值变为有限（分别为 15 和 9）。

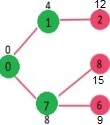
选取具有最小距离值且尚未包含在 SPT（不在 sptSET 中）的顶点。选取顶点 6。所以 sptSet 现在变成 {0， 1， 7， 6}。更新相邻顶点 6 的距离值。将更新顶点 5 和 8 的距离值。

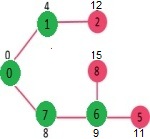
我们重复上述步骤，直到 sptSet 包含给定图形的所有顶点。最后，我们得到以下最短路径树（SPT）。

我们使用布尔数组 sptSet[] 来表示 SPT 中包含的顶点集。如果值 sptSet[v] 为真，则顶点 v 包含在 SPT 中，否则不包含。数组 dist[] 用于存储所有顶点的最短距离值。

算法的实现

golang

// F 代表两点之间不可达
const F = 10000
func dijkstra(graph [][]int, source int) []int {
   n := len(graph)
   if source >= n {
      return []int{}
   }
   dist := make([]int, n)
   visited := make([]bool, n)
   for i := 0; i < n; i++ {
      dist[i] = graph[source][i]
      visited[i] = false
   }
   dist[source] = 0
   visited[source] = true
​
   for i := 1; i < n; i++ {
      temMinDis := F
      curIdx := -1
      for j := 0; j < n; j++ {
         if !visited[j] && dist[j] < temMinDis {
            temMinDis = dist[j]
            curIdx = j
         }
      }
      visited[curIdx] = true
      dist[curIdx] = temMinDis
      for k := 0; k < n; k++ {
         if !visited[k] && dist[curIdx]+graph[curIdx][k] < dist[k] {
            dist[k] = dist[curIdx] + graph[curIdx][k]
         }
      }
   }
   return dist
}

Java

package graph.dijkstra;
​
import java.util.Arrays;
​
public class ShortestPathOfDijkstra {
    private static final int MAX = 10000;
​
    /**
     * 接受一个有向图的权重矩阵，和一个起点编号start（从0编号，顶点存在数组中)
     *
     * @param graph           graph
     * @param startPointIndex startPointIndex
     * @return 返回一个int[] 数组，表示从start到它的最短路径长度
     */
    public static int[] dijsktra(int[][] graph, int startPointIndex) {
        int length = graph.length;
        //标记当前该顶点的最短路径是否已经求出，true表示已经求出
        boolean[] visited = new boolean[length];
        //start点的最短距离已经求出
        for (int i = 0; i < graph.length; i++) {//初始化s集合，只有起始点
            if (i == startPointIndex) {
                visited[i] = true;
            } else {
                visited[i] = false;
            }
        }
​
        //存放从start到各个点的最短距离
        int[] shortDistance = new int[length];
​
        for (int i = 0; i < graph.length; i++) {//初始化，起始点到其他点的距离。
            shortDistance[i] = graph[startPointIndex][i];
        }
​
        //start到他本身的距离最短为0
        shortDistance[startPointIndex] = 0;
​
​
        //存放从start点到各点的最短路径的字符串表示
        String[] path = new String[length];
        for (int i = 0; i < length; i++) {
            path[i] = startPointIndex + "->" + i;
        }
​
        for (int count = 1; count < length; count++) {
            int k = -1;
            int dmin = MAX;
            for (int i = 0; i < length; i++) {
                if (!visited[i] && shortDistance[i] < dmin) {
                    dmin = shortDistance[i];
                    k = i;
                }
            }
            //选出一个距离start最近的未标记的顶点     将新选出的顶点标记为以求出最短路径，且到start的最短路径为dmin。
            shortDistance[k] = dmin;
            visited[k] = true;
            //以k为中间点，修正从start到未访问各点的距离
            for (int i = 0; i < length; i++) {
                if (!visited[i] && shortDistance[k] + graph[k][i] < shortDistance[i]) {
                    shortDistance[i] = shortDistance[k] + graph[k][i];
                    path[i] = path[k] + "->" + i;
                }
            }
        }
        for (int i = 0; i < length; i++) {
            System.out.println("从" + startPointIndex + "出发到" + i + "的最短路径为：" + path[i] + "=" + shortDistance[i]);
        }
        return shortDistance;
    }
​
    public static void main(String[] args) {
        int[][] graph = {
                {0, 4, 6, 6, MAX, MAX, MAX},
                {MAX, 0, 1, MAX, 7, MAX, MAX},
                {MAX, MAX, 0, MAX, 6, 4, MAX},
                {MAX, MAX, 2, 0, MAX, 5, MAX},
                {MAX, MAX, MAX, MAX, 0, MAX, 6},
                {MAX, MAX, MAX, MAX, 1, 0, 8},
                {MAX, MAX, MAX, MAX, MAX, MAX, MAX}};
        int start = 0;
        int[] dijsktra = dijsktra(graph, start);
        System.out.println(Arrays.toString(dijsktra));
    }
}