神经网络优化篇:详解其他正则化方法(Other regularization methods)
其他正则化方法
除了\(L2\)正则化和随机失活(dropout)正则化,还有几种方法可以减少神经网络中的过拟合:
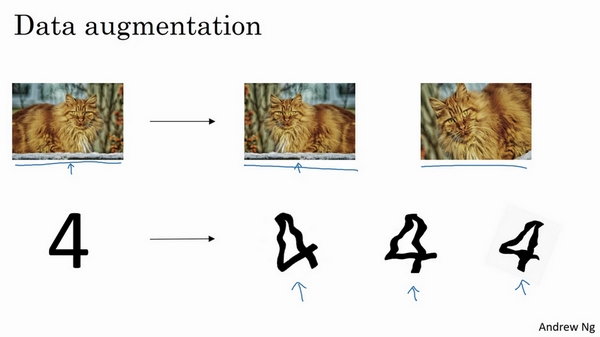
一.数据扩增
假设正在拟合猫咪图片分类器,如果想通过扩增训练数据来解决过拟合,但扩增数据代价高,而且有时候无法扩增数据,但可以通过添加这类图片来增加训练集。例如,水平翻转图片,并把它添加到训练集。所以现在训练集中有原图,还有翻转后的这张图片,所以通过水平翻转图片,训练集则可以增大一倍,因为训练集有冗余,这虽然不如额外收集一组新图片那么好,但这样做节省了获取更多猫咪图片的花费。

除了水平翻转图片,也可以随意裁剪图片,这张图是把原图旋转并随意放大后裁剪的,仍能辨别出图片中的猫咪。
通过随意翻转和裁剪图片,可以增大数据集,额外生成假训练数据。和全新的,独立的猫咪图片数据相比,这些额外的假的数据无法包含像全新数据那么多的信息,但这么做基本没有花费,代价几乎为零,除了一些对抗性代价。以这种方式扩增算法数据,进而正则化数据集,减少过拟合比较廉价。

像这样人工合成数据的话,要通过算法验证,图片中的猫经过水平翻转之后依然是猫。大家注意,并没有垂直翻转,因为不想上下颠倒图片,也可以随机选取放大后的部分图片,猫可能还在上面。
对于光学字符识别,还可以通过添加数字,随意旋转或扭曲数字来扩增数据,把这些数字添加到训练集,它们仍然是数字。为了方便说明,对字符做了强变形处理,所以数字4看起来是波形的,其实不用对数字4做这么夸张的扭曲,只要轻微的变形就好,做成这样是为了让大家看的更清楚。实际操作的时候,通常对字符做更轻微的变形处理。因为这几个4看起来有点扭曲。所以,数据扩增可作为正则化方法使用,实际功能上也与正则化相似。
二.early stopping
还有另外一种常用的方法叫作early stopping,运行梯度下降时,可以绘制训练误差,或只绘制代价函数\(J\)的优化过程,在训练集上用0-1记录分类误差次数。呈单调下降趋势,如图。
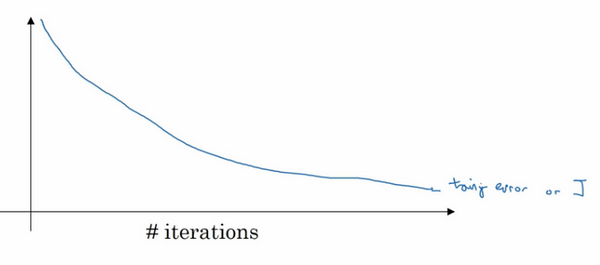
因为在训练过程中,希望训练误差,代价函数\(J\)都在下降,通过early stopping,不但可以绘制上面这些内容,还可以绘制验证集误差,它可以是验证集上的分类误差,或验证集上的代价函数,逻辑损失和对数损失等,会发现,验证集误差通常会先呈下降趋势,然后在某个节点处开始上升,early stopping的作用是,会说,神经网络已经在这个迭代过程中表现得很好了,在此停止训练吧,得到验证集误差,它是怎么发挥作用的?

当还未在神经网络上运行太多迭代过程的时候,参数\(w\)接近0,因为随机初始化\(w\)值时,它的值可能都是较小的随机值,所以在长期训练神经网络之前\(w\)依然很小,在迭代过程和训练过程中\(w\)的值会变得越来越大,比如在这儿,神经网络中参数\(w\)的值已经非常大了,所以early stopping要做就是在中间点停止迭代过程,得到一个\(w\)值中等大小的弗罗贝尼乌斯范数,与\(L2\)正则化相似,选择参数w范数较小的神经网络,但愿的神经网络过度拟合不严重。
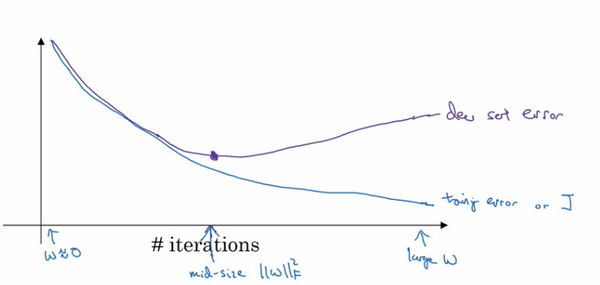
术语early stopping代表提早停止训练神经网络,训练神经网络时,有时会用到early stopping,但是它也有一个缺点,来了解一下。
认为机器学习过程包括几个步骤,其中一步是选择一个算法来优化代价函数\(J\),有很多种工具来解决这个问题,如梯度下降,后面会介绍其它算法,例如Momentum,RMSprop和Adam等等,但是优化代价函数\(J\)之后,也不想发生过拟合,也有一些工具可以解决该问题,比如正则化,扩增数据等等。
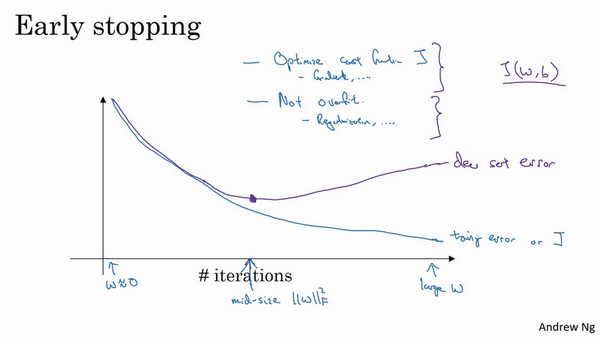
在机器学习中,超级参数激增,选出可行的算法也变得越来越复杂。发现,如果用一组工具优化代价函数\(J\),机器学习就会变得更简单,在重点优化代价函数\(J\)时,只需要留意\(w\)和\(b\),\(J(w,b)\)的值越小越好,只需要想办法减小这个值,其它的不用关注。然后,预防过拟合还有其他任务,换句话说就是减少方差,这一步用另外一套工具来实现,这个原理有时被称为“正交化”。思路就是在一个时间做一个任务。
但对来说early stopping的主要缺点就是不能独立地处理这两个问题,因为提早停止梯度下降,也就是停止了优化代价函数\(J\),因为现在不再尝试降低代价函数\(J\),所以代价函数\(J\)的值可能不够小,同时又希望不出现过拟合,没有采取不同的方式来解决这两个问题,而是用一种方法同时解决两个问题,这样做的结果是要考虑的东西变得更复杂。
如果不用early stopping,另一种方法就是\(L2\)正则化,训练神经网络的时间就可能很长。发现,这导致超级参数搜索空间更容易分解,也更容易搜索,但是缺点在于,必须尝试很多正则化参数\(\lambda\)的值,这也导致搜索大量\(\lambda\)值的计算代价太高。
Early stopping的优点是,只运行一次梯度下降,可以找出\(w\)的较小值,中间值和较大值,而无需尝试\(L2\)正则化超级参数\(\lambda\)的很多值。
虽然\(L2\)正则化有缺点,可还是有很多人愿意用它。吴恩达老师个人更倾向于使用\(L2\)正则化,尝试许多不同的\(\lambda\)值,假设可以负担大量计算的代价。而使用early stopping也能得到相似结果,还不用尝试这么多\(\lambda\)值。
神经网络优化篇:详解其他正则化方法(Other regularization methods)的更多相关文章
- 【初级】linux rm 命令详解及使用方法实战
rm:删除命令 前言: windows中的删除命令大家都不陌生,linux中的删除命令和windows中有一个共同特点,那就是危险,前两篇linux mkdir 命令详解及使用方法实战[初级]中我们就 ...
- PHP函数篇详解十进制、二进制、八进制和十六进制转换函数说明
PHP函数篇详解十进制.二进制.八进制和十六进制转换函数说明 作者: 字体:[增加 减小] 类型:转载 中文字符编码研究系列第一期,PHP函数篇详解十进制.二进制.八进制和十六进制互相转换函数说明 ...
- PHP开发中常见的安全问题详解和解决方法(如Sql注入、CSRF、Xss、CC等
页面导航: 首页 → 网络编程 → PHP编程 → php技巧 → 正文内容 PHP安全 PHP开发中常见的安全问题详解和解决方法(如Sql注入.CSRF.Xss.CC等) 作者: 字体:[增加 减小 ...
- 走向DBA[MSSQL篇] 详解游标
原文:走向DBA[MSSQL篇] 详解游标 前篇回顾:上一篇虫子介绍了一些不常用的数据过滤方式,本篇详细介绍下游标. 概念 简单点说游标的作用就是存储一个结果集,并根据语法将这个结果集的数据逐条处理. ...
- Scala进阶之路-Scala函数篇详解
Scala进阶之路-Scala函数篇详解 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 一.传值调用和传名调用 /* @author :yinzhengjie Blog:http: ...
- 【初级】linux pwd 命令详解及使用方法实战
pwd:查看当前工作目录 前言: Linux中用 pwd 命令来查看”当前工作目录“的完整路径,就是经常提及的所在目录,多用在生产环境多级目录中查看当前所在路径,使用此命令能给运维人员/操作人员带来很 ...
- 【初级】linux mkdir 命令详解及使用方法实战
mkdir命令详解及使用方法实战 名称 MKDIR 是 make directories 的缩写 使用方法 mkdir [选项(如-p)] ...目录名称(及子目录注意用分隔符隔开)... 如使 ...
- ThinkPHP函数详解:session方法
ThinkPHP函数详解:session方法 Session方法用于Session 设置.获取.删除和管理操作. Session 用于Session 设置.获取.删除和管理操作 用法 sessi ...
- 转:JAVAWEB开发之权限管理(二)——shiro入门详解以及使用方法、shiro认证与shiro授权
原文地址:JAVAWEB开发之权限管理(二)——shiro入门详解以及使用方法.shiro认证与shiro授权 以下是部分内容,具体见原文. shiro介绍 什么是shiro shiro是Apache ...
- tomcat常用配置详解和优化方法
tomcat常用配置详解和优化方法 参考: http://blog.csdn.net/zj52hm/article/details/51980194 http://blog.csdn.net/wuli ...
随机推荐
- 云上的甜蜜早安:腾讯云云函数助力PHP打造女友专属每日推送
用腾讯云的云函数做一个微信公众号早安,每天定时发送早安给你的女朋友! 1.首先我们登录腾讯云,在搜索栏搜索云函数,或直接用这个链接进入curl.qcloud.com/Td0IkpmD 2.进入云函数, ...
- daemonset应用创建了,但是没有pod被调度起来
环境: k8s版本1.25.2 一个master 两个node节点 集群节点全部允许调度(无污点),且资源充足. 操作系统版本: Ubuntu22.01 排查思路: 查看kubelet 日志,和c ...
- Intrusion Detection Using Convolutional Neural Networks for Representation Learning 笔记
Intrusion Detection Using Convolutional Neural Networks for Representation Learning 2.2 实验数据的预处理 为了确 ...
- mac应用已损坏无法打开
sudo xattr -r -d com.apple.quarantine /User/name/yourapp # '/User/name/yourapp' 替换成你自己要安装的 mac 应用地址 ...
- 我在前端写Java SpringBoot项目
前言 玩归玩,闹归闹,别拿 C端 开玩笑! 这里不推荐大家把Node服务作为C端服务,毕竟它是单线程多任务 机制. 这一特性是 Javascript 语言设计之初,就决定了它的使命 - Java &g ...
- Java并发编程和多线程的区别
并发编程: 并发编程是一种编程范式,它关注的是编写能够正确和高效处理多个并发任务的程序.并发编程不仅包括多线程,还包括了处理多个独立任务的各种技术和模式,如进程.协程.分布式编程等.并发编程的目标是实 ...
- 小白也能看懂的 AUC 曲线详解
小白也能看懂的 AUC 曲线详解 简介 上篇文章 小白也能看懂的 ROC 曲线详解 介绍了 ROC 曲线.本文介绍 AUC.AUC 的全名为Area Under the ROC Curve,即 ROC ...
- 图片调整大小,图片改变像素,用win10自带的工具就够了
A:大哥大哥,你会PS吗? 内心:好家伙,什么大项目,都用上ps了,还好大学的时候学过一点点. 我:嗯嗯,会一点,怎么了 A:你看,帮我调整一下图片呗 内心:哈哈,又能看到某人的照片了.... 我:害 ...
- ruoyi框架里面设置登录超时时间不能生效
问题 项目使用到了ruoyi框架,给登录超时限制了12小时,但是每次几个小时后就提示过期,要求再登录一次. 首先怀疑是不是redis内存淘汰策略出现了问题. 先使用一下的命令 systemctl st ...
- [转载]R2: 已解释和未解释的方差
估计值的方差与总体方差之间的差异就是回归方程对方差的解释率.试举一例,如图 1,身高与体重的回归线显示身高与体重之间呈正相关,Mr. Y身高76英寸体重220磅(图 1中插图.cdr的红点),他与体重 ...
