神经网络基础篇：Python 中的广播（Broadcasting in Python）

Python 中的广播

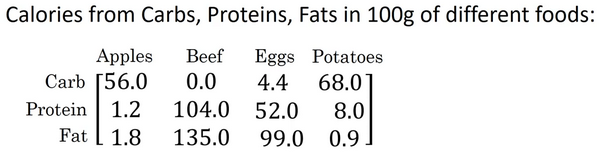
这是一个不同食物(每100g)中不同营养成分的卡路里含量表格，表格为3行4列，列表示不同的食物种类，从左至右依次为苹果，牛肉，鸡蛋，土豆。行表示不同的营养成分，从上到下依次为碳水化合物，蛋白质，脂肪。

那么，现在想要计算不同食物中不同营养成分中的卡路里百分比。

现在计算苹果中的碳水化合物卡路里百分比含量，首先计算苹果（100g）中三种营养成分卡路里总和56+1.2+1.8

= 59，然后用56/59 = 94.9%算出结果。

可以看出苹果中的卡路里大部分来自于碳水化合物，而牛肉则不同。

对于其他食物，计算方法类似。首先，按列求和，计算每种食物中（100g）三种营养成分总和，然后分别用不用营养成分的卡路里数量除以总和，计算百分比。

那么，能否不使用for循环完成这样的一个计算过程呢？

假设上图的表格是一个4行3列的矩阵\(A\)，记为 \(A_{3\times 4}\)，接下来要使用Python的numpy库完成这样的计算。打算使用两行代码完成，第一行代码对每一列进行求和，第二行代码分别计算每种食物每种营养成分的百分比。

在jupyter notebook中输入如下代码，按shift+Enter运行，输出如下。

下面使用如下代码计算每列的和，可以看到输出是每种食物(100g)的卡路里总和。

其中sum的参数axis=0表示求和运算按列执行，之后会详细解释。

接下来计算百分比，这条指令将 \(3\times 4\)的矩阵\(A\)除以一个\(1 \times 4\)的矩阵，得到了一个 \(3 \times 4\)的结果矩阵，这个结果矩阵就是要求的百分比含量。

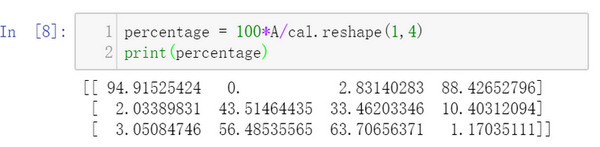
下面再来解释一下A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行，在numpy中，0轴是垂直的，也就是列，而1轴是水平的，也就是行。

而第二个A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用 \(3 \times 4\)的矩阵\(A\)除以 \(1 \times 4\)的矩阵\(cal\)。技术上来讲，其实并不需要再将矩阵\(cal\) reshape(重塑)成 \(1 \times 4\)，因为矩阵\(cal\)本身已经是 \(1 \times 4\)了。但是当写代码时不确定矩阵维度的时候，通常会对矩阵进行重塑来确保得到想要的列向量或行向量。重塑操作reshape是一个常量时间的操作，时间复杂度是\(O(1)\)，它的调用代价极低。

那么一个 \(3 \times 4\) 的矩阵是怎么和 \(1 \times 4\)的矩阵做除法的呢？让来看一些更多的广播的例子。

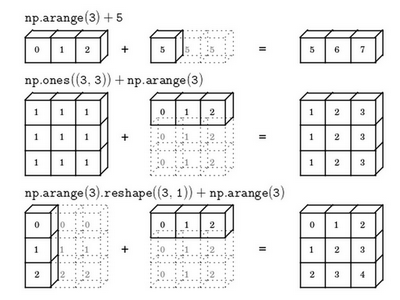
在numpy中，当一个 \(4 \times 1\)的列向量与一个常数做加法时，实际上会将常数扩展为一个 \(4 \times 1\)的列向量，然后两者做逐元素加法。结果就是右边的这个向量。这种广播机制对于行向量和列向量均可以使用。

再看下一个例子。

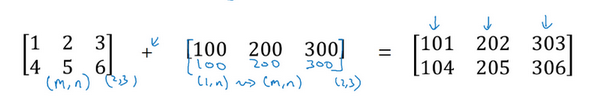
用一个 \(2 \times 3\)的矩阵和一个 \(1 \times 3\) 的矩阵相加，其泛化形式是 \(m \times n\) 的矩阵和 \(1 \times n\)的矩阵相加。在执行加法操作时，其实是将 \(1 \times n\) 的矩阵复制成为 \(m \times n\) 的矩阵，然后两者做逐元素加法得到结果。针对这个具体例子，相当于在矩阵的第一列加100，第二列加200，第三列加300。这就是在前面的计算卡路里百分比的广播机制，只不过这里是除法操作（广播机制与执行的运算种类无关）。

下面是最后一个例子

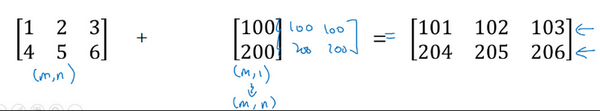
这里相当于是一个 \(m \times n\) 的矩阵加上一个 \(m \times 1\) 的矩阵。在进行运算时，会先将 \(m \times 1\) 矩阵水平复制 \(n\) 次，变成一个 \(m \times n\) 的矩阵，然后再执行逐元素加法。

广播机制的一般原则如下：

这里先说一下本人对numpy广播机制的理解。

首先是numpy广播机制

如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。

后缘维度的轴长度：A.shape[-1] 即矩阵维度元组中的最后一个位置的值

对于博客中卡路里计算的例子，矩阵 \(A_{3,4}\) 后缘维度的轴长度是4，而矩阵 \(cal_{1,4}\) 的后缘维度也是4，则他们满足后缘维度轴长度相符，可以进行广播。广播会在轴长度为1的维度进行，轴长度为1的维度对应axis=0，即垂直方向，矩阵 \(\text{cal}_{1,4}\) 沿axis=0(垂直方向)复制成为 \(\text{cal_temp}_{3,4}\) ，之后两者进行逐元素除法运算。

现在解释上图中的例子

矩阵 \(A_{m,n}\) 和矩阵 \(B_{1,n}\) 进行四则运算，后缘维度轴长度相符，可以广播，广播沿着轴长度为1的轴进行，即 \(B_{1,n}\) 广播成为 \({B_{m,n}}'\) ，之后做逐元素四则运算。

矩阵 \(A_{m,n}\) 和矩阵 \(B_{m,1}\) 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着轴长度为1的轴进行，即 \(B_{m,1}\) 广播成为 \({B_{m,n}}'\) ，之后做逐元素四则运算。

矩阵 \(A_{m,1}\) 和常数$ R$ 进行四则运算，后缘维度轴长度不相符，但其中一方轴长度为1，可以广播，广播沿着缺失维度和轴长度为1的轴进行，缺失维度就是axis=0,轴长度为1的轴是axis=1，即\(R\)广播成为 \({B_{m,1}}'\) ，之后做逐元素四则运算。

最后，对于Matlab/Octave 有类似功能的函数bsxfun。

总结一下broadcasting，可以看看下面的图：