2019年第十届蓝桥杯国赛C++C组

蓝桥杯历年国赛真题汇总：Here

统一声明

如果不写默认带有常用头文件

如果不表明主函数默认表示在 void solve(){}

默认使用

using namespace std;
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using ll = long long;

填空题答案速览 (个人解题答案，如果有误欢迎指正)

1. 139311
2. 180414
3. 26287
4. 47373

试题 A: 奇数倍数

答案：139311

void solve() {
    for (int i = 2019 * 2;; i += 2019) {
        int j = i, f = 1;
        while (j) {
            if ( !((j % 10) & 1)) {f = 0 ; break;}
            j /= 10;
        }
        if (f) {cout << i << "\n"; return ;}
    }
}

试题 B: 递增序列

【问题描述】

对于一个字母矩阵，我们称矩阵中的一个三升序列是指在矩阵中找到三个 字母，它们在同一行，同一列，或者在同一 45 度的斜线上，这三个字母从左向 右看、或者从上向下看是递增的。

例如，如下矩阵中

YQPD
BKEZ
AFYV

有BKZ、BEZ、AFY、AFV、AKP、DEF 等 6 个三升序列。注意当三个字母 是从左下到右上排列时，从左向右看和从上向下看是不同的顺序。

对于下面的 30 行 50 列的矩阵，请问总共有多少个三升序列？（如果你把 以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在 试题目录下有一个文件 inc.txt，内容与下面的文本相同）

VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG
SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF
ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA
BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL
YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH
ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU
XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR
ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG
MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA
VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF
GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC
EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK
PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW
CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP
RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS
PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR
JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL
YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP
HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN
DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF
LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW
CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ
IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI
ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB
HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP
FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS
VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ
BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR
RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY
ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXX

答案：180414

#include<bits/stdc++.h>
using namespace std;
char text[30][500];
void copytext() {
    char c[500];
    int line = 0;
    FILE *fp = fopen("inc.txt", "r");
    if (fp == NULL) {
        cout << "failed to open file!" << endl;
    } else {
        while (fgets(c, 500, fp))
            strcpy(text[line++], c);
    }
    fclose(fp);
}
int main() {
    int temp1, temp2;
    int hang = 30; int lie = 50;
    cin >> hang >> lie;
    int i, j, k, r = 0, count = 0;
    copytext();
    //求每行的三升序列
    for (i = 0; i < hang; i++)
        for (j = 0; j < lie; j++)
            for (k = j + 1; k < lie; k++)
                if (text[i][j] < text[i][k] && text[i][k] < 90)
                    for (r = k + 1; r < lie; r++)
                        if (text[i][k] < text[i][r])
                            count++;
    //求每列的三升序列
    for (i = 0; i < lie; i++)
        for (j = 0; j < hang; j++)
            for (k = j + 1; k < hang; k++)
                if (text[j][i] < text[k][i] && text[k][i] < 90)
                    for (r = k + 1; r < hang; r++)
                        if (text[k][i] < text[r][i])
                            count++;
    //求左下到右上对角线的三升序列
    for (i = 2; i < hang; i++)
        for (j = 0; j < lie; j++) {
            k = j; r = i;
            while (r - 1 >= 0 && k + 1 < lie) {
                if (text[i][j] < text[r - 1][k + 1] && text[r - 1][k + 1] < 90) {
                    temp1 = r - 2; temp2 = k + 2;
                    while (temp1 >= 0 && temp2 < lie) {
                        if (text[r - 1][k + 1] < text[temp1][temp2])
                            count++;
                        temp1--; temp2++;
                    }
                }
                k++; r--;
            }
        }
    //求右上到左下对角线的三升序列
    for (i = 0; i < hang; i++)
        for (j = 2; j < lie; j++) {
            k = j; r = i;
            while (k - 1 >= 0 && r + 1 < hang) {
                if (text[i][j] < text[r + 1][k - 1] && text[r + 1][k - 1] < 90) {
                    temp1 = r + 2; temp2 = k - 2;
                    while (temp2 >= 0 && temp1 < hang) {
                        if (text[r + 1][k - 1] < text[temp1][temp2])
                            count++;
                        temp2--; temp1++;
                    }
                }
                k--; r++;
            }
        }
    //求左上到右下对角线的三升序列
    for (i = 0; i < hang; i++)
        for (j = 0; j < lie; j++) {
            k = j; r = i;
            while (r + 1 < hang && k + 1 < lie) {
                if (text[i][j] < text[r + 1][k + 1] && text[r + 1][k + 1] < 90) {
                    temp1 = r + 2; temp2 = k + 2;
                    while (temp1 < hang && temp2 < lie) {
                        if (text[r + 1][k + 1] < text[temp1][temp2])
                            count++;
                        temp1++; temp2++;
                    }
                }
                k++; r++;
            }
        }
    cout << count << endl;
    return 0;
}

试题 C: 平方拆分

答案：26287

深搜，要需要注意一下枚举起点为 \(1\) 而不是 \(0\)

ll sum;
void dfs(int num, int Min, int Max) {
    if (num < 0)return ;
    if (num == 0) {
        sum++;
        return ;
    }
    for (int i = Min; i < Max; ++i)
        dfs(num - i * i, i + 1, Max);
}
void solve() {
    dfs(2019, 1, 45);
    cout << sum;
}

试题 D: 最优旅行

【问题描述】

中国的高铁四通八达，乘坐方便，小明经常乘坐高铁在城市间旅游。 

现在，小明又有了一个长假，他打算继续乘坐高铁旅游。这次，他打算到 下面的城市旅游。

上海、广州、长沙、西安、杭州、济南、成都、南京、昆明、郑州、天津、 太原、武汉、重庆、南昌、长春、沈阳、贵阳、福州。 

小明打算从北京出发，游览以上每个城市正好一次，最终回到北京。在每 个城市（除北京外），小明都至少停留 24 小时。而当小明决定从一个城市去往 另一个城市时，他只会选择有直接高铁连接的城市，不会在中途换乘转车。 

在试题目录下有一个文件 trip.txt 保存了小明可以选择的车次，小明不会 选择其他车次。 小明出发的时间是第 1 天的中午 12:00。

请问，小明游览完以上城市正好一 次，最终回到北京，最快需要多少分钟（请注意单位为分钟）

答案：

// trip.txt
车次  出发站 到达站 出发时间 到达时间
G169   北京   上海   16:40   22:35
G21    北京   上海   19:08   23:40
G18    上海   北京   17:55   22:36
G68    广州   北京   11:13   21:10
G67    北京   广州   12:13   22:19
G1305  上海   广州   15:25   23:38
G86    广州   上海   08:00   14:50
G6122  广州   长沙   21:00   23:36
G6117  长沙   广州   17:55   20:39
G502   长沙   北京   07:36   14:24
G503   北京   长沙   14:41   21:14
G1359  上海   长沙   15:37   20:59
G1348  长沙   上海   09:00   13:41
G362   西安   上海   08:49   14:45
G1936  上海   西安   16:12   22:54
G87    北京   西安   14:00   18:20
G88    西安   北京   13:30   17:55
G98    西安   广州   09:57   17:39
G836   广州   西安   11:24   20:09
G1404  广州   杭州   15:56   23:25
G20    杭州   北京   07:48   12:20
G39    北京   杭州   19:04   23:22
G7355  上海   杭州   21:30   22:28
G7558  杭州   上海   07:06   08:12
G300   济南   上海   06:50   11:40
G333   北京   济南   19:55   21:55
G336   济南   北京   07:45   09:33
G2056  广州   济南   08:05   18:34
G2058  济南   广州   10:14   20:49
G350   成都   北京   07:00   14:46
G89    北京   成都   06:53   14:38
G1888  成都   南京   11:28   22:00
G7180  上海   南京   10:05   11:29
G7003  南京   上海   08:00   09:39
G7613  南京   杭州   16:19   17:40
G7604  杭州   南京   12:09   13:30
G1540  昆明   南京   10:20   21:14
G1539  南京   昆明   09:05   19:40
G2883  成都   昆明   08:51   14:29
G2884  昆明   成都   12:16   17:57
G1538  昆明   郑州   08:46   18:48
G1537  郑州   昆明   10:38   20:49
G2001  郑州   西安   07:52   10:24
G2002  西安   郑州   08:10   10:29
G2231  西安   重庆   17:06   22:56
G2232  重庆   西安   07:05   12:37
G8594  重庆   成都   06:50   08:07
G8599  成都   重庆   22:12   23:29
G1709  天津   重庆   08:05   19:39
G1710  重庆   天津   10:49   22:45
G8901  北京   天津   22:10   22:45
G8928  天津   北京   19:08   19:46
G2609  天津   太原   10:40   14:15
G2610  太原   天津   14:43   18:12
G1954  太原   上海   12:26   21:17
G1952  上海   太原   08:10   17:28
G686   郑州   太原   13:17   17:16
G688   太原   郑州   17:38   21:38
G1864  太原   杭州   12:50   21:10
G1862  杭州   太原   07:14   15:50
G91    北京   太原   08:40   11:07
G92    太原   北京   08:33   11:00
G694   太原   武汉   16:37   22:29
G692   武汉   太原   09:48   16:00
G1722  武汉   上海   08:00   11:53
G1720  上海   武汉   13:51   17:50
G858   西安   武汉   15:18   19:48
G856   武汉   西安   09:17   14:27
G365   天津   武汉   14:56   20:41
G366   武汉   天津   14:30   20:32
G294   长沙   天津   08:47   16:56
G292   天津   长沙   10:58   18:50
G696   长沙   太原   09:23   17:55
G698   太原   长沙   10:46   18:18
G1391  杭州   昆明   11:43   22:53
G1392  昆明   杭州   09:06   20:18
G1514  昆明   南昌   16:00   22:54
G1511  南昌   昆明   08:25   15:38
G1462  南昌   杭州   12:24   15:28
G1451  杭州   南昌   12:30   15:26
G1244  济南   长春   07:42   15:07
G1242  长春   济南   15:33   22:35
G8033  沈阳   长春   06:42   08:40
G1290  长沙   长春   07:21   21:09
G1292  长春   长沙   08:47   22:08
G400   长春   北京   08:32   14:48
G399   北京   长春   15:20   21:45
G1886  南京   成都   08:07   17:54
G579   南京   长沙   09:27   14:10
G580   长沙   南京   15:53   20:40
G1484  贵阳   南京   07:58   18:02
G2335  南京   贵阳   12:07   21:58
G2105  长沙   贵阳   13:17   16:55
G2116  贵阳   长沙   08:11   11:26
G2201  郑州   成都   07:10   13:19
G2212  成都   郑州   16:57   23:04
G1814  上海   郑州   14:15   18:12
G370   郑州   上海   07:33   12:02
G1274  武汉   沈阳   07:23   19:03
G1272  沈阳   武汉   07:32   19:20
G2869  重庆   昆明   07:43   11:55
G2870  昆明   重庆   14:52   19:09
G1335  重庆   上海   08:48   20:56
G1333  上海   重庆   11:39   23:29
G1759  南昌   重庆   07:08   14:45
G1761  重庆   南昌   15:12   22:23
G1493  南京   南昌   13:00   17:21
G1496  南昌   南京   09:04   13:25
G5314  南昌   福州   08:13   11:09
G5312  福州   南昌   18:30   21:25
G1256  长春   上海   11:53   22:54
G1258  上海   长春   09:08   20:05
G1284  沈阳   成都   07:02   21:47
G1282  成都   沈阳   09:06   23:13
G217   北京   沈阳   13:30   17:15
G218   沈阳   北京   08:11   11:58
G2604  沈阳   太原   15:34   23:00
G2602  太原   沈阳   07:44   15:14
G8664  贵阳   成都   19:15   22:35
G8691  成都   贵阳   11:11   14:31
G2958  贵阳   广州   14:03   20:26
G2960  广州   贵阳   07:27   13:43
G1521  武汉   贵阳   08:01   13:25
G1524  贵阳   武汉   14:23   19:33
G1609  福州   广州   08:16   14:15
G1607  广州   福州   14:55   21:05
G1696  昆明   福州   11:11   22:02
G1698  福州   昆明   08:41   19:28
G1636  福州   上海   12:26   16:55
G1631  上海   福州   07:54   12:15
G1642  福州   杭州   14:45   18:32
G1641  杭州   福州   18:55   22:38

答案：47373 (个人答案)

这道题一开始以为要跑最短路之类，但写法会很麻烦，参考了一下 Try one try 大佬的思路

思路：dfs+最优性剪枝，具体思路见代码，注明得非常清楚。

注意：城市为汉字（字符串），所以不便于转化图的顶点。我的方法：将每个城市用1-20的整数代表，从而方便代表图的端点。

补充：题干说明了中途经过的每一个城市（除北京），都需要休息24h以上，那么经过每个城市都需要加上1440分钟，也就是最终时间加上19*1440。为什么？

例子：

前一班15:30到，下一班16.30出发 ，显然今天是不可能走的了（时间间隔才1h），需要等到明天16.30才走。即需要休息一天+24h

前一班15.30到，下一班08.30出发 ，显然到第二天早上8.30也没有休息到24h需要再等1天，等到第三天的8.30才能出发， 所以也需要休息一天+24h

下面直接引用一下大佬的代码用作学习了。

#include <bits/stdc++.h>
using namespace std;
/*
    将城市转化数字，从而转化为图论结构
    北京--1  上海--2  广州--3  长沙--4  西安--5 杭州--6
    济南--7  成都--8  南京--9  昆明--10  郑州--11  天津--12
    太原--13 武汉--14 重庆--15 南昌--16  长春--17  沈阳--18
    贵阳--19 福州--20
*/
struct Node {
    int e;  //终点
    int starttime, endtime; //起始时间，到达时间(转换为分钟表示)
    int cost; // 运行时间
    Node(int des, int startt, int endt, int time): e(des), starttime(startt), endtime(endt), cost(time) {}
    Node() {}
};
vector<vector<Node> >  G(25); //存放所有班次信息
map<string, int> m;
long long mintime = 0x3f3f3f3f3f3f3f;
long long totaltime = 0;
int vis[25];  //标志去过哪些城市了(每个城市只能去一次，除了北京）
void INIT() {
    m.insert(make_pair("北京", 1));
    m.insert(make_pair("上海", 2));
    m.insert(make_pair("广州", 3));
    m.insert(make_pair("长沙", 4));
    m.insert(make_pair("西安", 5));
    m.insert(make_pair("杭州", 6));
    m.insert(make_pair("济南", 7));
    m.insert(make_pair("成都", 8));
    m.insert(make_pair("南京", 9));
    m.insert(make_pair("昆明", 10));
    m.insert(make_pair("郑州", 11));
    m.insert(make_pair("天津", 12));
    m.insert(make_pair("太原", 13));
    m.insert(make_pair("武汉", 14));
    m.insert(make_pair("重庆", 15));
    m.insert(make_pair("南昌", 16));
    m.insert(make_pair("长春", 17));
    m.insert(make_pair("沈阳", 18));
    m.insert(make_pair("贵阳", 19));
    m.insert(make_pair("福州", 20));
    memset(vis, 0, sizeof(vis));
}
void dfs(int s, int endt, int len) { //s为起点城市，endt为到达此城市的时间，len为当前旅游过哪些城市了
    if (s == 1 && len > 0) { //到达北京就要回溯 (除了开始从北京出发)
        bool flag = true;
        for (int i = 1; i <= 20; i++) //检查是否旅游完毕
            if (vis[i] == 0)
                flag = false;
        vis[1] = 0; //北京始终允许反复访问（在北京多次中转）
        if (flag) //走遍所有地点（19个旅游城市+1个终点城市北京）
            mintime = min(mintime, totaltime);
        /*
        注：如果直接if(len==20)判断的话，会忽略掉可以经过北京中转的情况，
            虽然此题结果经过北京中转不会使时间减少，但是我们设计程序应该考虑全面
        */
        return;
    }
    for (int i = 0; i < G[s].size(); i++) {
        Node r = G[s][i];
        if (vis[r.e] == 0) { //目的城市没去过
            vis[r.e] = 1;
            long long temp = totaltime;
            //time1: 此班车的运行时间
            totaltime += r.cost;
            //time2: 班次间隔时间(24h内)
            if (s != 1 && r.starttime > endt) //此班车出发时间和上一班结束时间的关系
                totaltime += r.starttime - endt; //休息时间（当日）
            if (s != 1 && r.starttime < endt)
                totaltime += r.starttime - endt + 1440; //跨日
            //time3: 从北京出发时的等车时间
            if (s == 1) {
                if (r.starttime > 720) //十二点出发
                    totaltime += r.starttime - 720;
                else
                    totaltime -= r.starttime - 720 + 1440; //只有等到明天才能出发了
            }
            //最优性剪枝:不剪枝会花跑很久
            if (totaltime > mintime) {
                totaltime = temp;
                continue;
            }
            dfs(r.e, r.endtime, len + 1);
            vis[r.e] = 0;
            totaltime = temp;
        }
    }
}
int main() {
    INIT();
    //freopen("trip.txt","r",stdin); //注意：从文件中读取文字信息会发生乱码
    //读入某行信息也可以使用getline(cin,str);
    string str;
    for (int i = 1; i <= 5; i++) //读入第一行无用数据
        cin >> str;
    for (int i = 1; i <= 132; i++) { //共有132班车
        cin >> str; //去掉无用的班次名字
        string src, des; //起始站-->终点站
        string s, t;    //出发时间-->到达时间
        cin >> src >> des >> s >> t;
        //换算时间为分钟表示
        int a, b;
        a = (s[0] - '0') * 600 + (s[1] - '0') * 60 + (s[3] - '0') * 10 + (s[4] - '0');
        b = (t[0] - '0') * 600 + (t[1] - '0') * 60 + (t[3] - '0') * 10 + (t[4] - '0');
        int cost; //运行时间
        if (a < b)
            cost = b - a;
        else
            cost = b - a + 1440; //+1天
        //存入图中
        G[m[src]].push_back(Node(m[des], a, b, cost));
    }
    //检验所有班次以及城市信息的录入情况
    //for(int i=0;i<25;i++)
    //  for(int j=0;j<G[i].size();j++)
    //  {
    //      Node r=G[i][j];
    //      cout<<i<<" "<<r.e<<" "<<r.starttime<<" "<<r.endtime<<" "<<r.cost<<endl;
    //  }
    dfs(1, 0, 0); //从北京出发
    mintime += 1440 * 19; //加上19天的停留(如果经过北京中转，不会停留24h)
    /*任意两趟班次之间：前一班的到达时间 到 下一班的发车时间间隔都是小于24h
      例如：前一班15:30到，下一班16.30出发  需要休息一天+24h
            前一班15.30到，下一班08.30出发  也需要休息一天+24h
    */
    cout << mintime;
    return 0;
}
//注意：班次信息为每天固定发车，即每天都会同一时间发同一班车
//ANS : 47373

试题 E: 骰子制造

答案：

试题 F: 最长子序列

我们称一个字符串 S 包含字符串 T 是指 T 是 S 的一个子序列，即可以从 字符串 S 中抽出若干个字符，它们按原来的顺序组合成一个新的字符串与 T 完 全一样。

给定两个字符串 S 和 T，请问 T 中从第一个字符开始最长连续多少个字符 被 S 包含？

【输入格式】

输入两行，每行一个字符串。第一行的字符串为 S，第二行的字符串为 T。 两个字符串均非空而且只包含大写英文字母。

【输出格式】

输出一个整数，表示答案。

【样例输入】

ABCDEABCD
AABZ

【样例输出】

3

对于 20% 的评测用例，\(1 ≤ |T| ≤ |S | ≤ 20\)；

对于 40% 的评测用例，\(1 ≤ |T| ≤ |S | ≤ 100\)；

对于所有评测用例，\(1 ≤ |T| ≤ |S | ≤ 1000\)。

---

【解法一】暴力

void solve() {
    string a, b; cin >> a >> b;
    int n = a.size(), m = b.size();
    int cnt = 0;
    for (int i = 0; i < m; ++i)
        for (int j = 0; j < n; ++j)
            if (b[i] == a[j])cnt++, i++;
    cout << cnt;
}

【解法二】DP

int F(string text1, string text2) {
    //  先计算两条字符串的长度
    int m = text1.size();
    int n = text2.size();
    //  构建dp矩阵  默认初始值0
    //  这里会多扩建一边和一列
    //  因为dp[i][j]的含义是：对于 s1[1..i] 和 s2[1..j]，它们的LCS长度是 dp[i][j]。
    //  所以当i或者j为零时  LCS的长度默认为0
    vector< vector<int> > dp ( m + 1, vector<int> ( n + 1, 0 ) );
    //  状态转移
    //  i、j都从1开始遍历  因为下面的操作中都会-1  相当于从0开始
    for ( int i = 1 ; i < m + 1 ; i++ ) {
        for ( int j = 1 ; j < n + 1 ; j++ ) {
            //  如果text1和text2相同
            //  就在它们的前一位基础上加一
            //  如果不同  只能在之前的两者中去最大
            dp[i][j] = (text1[i - 1] == text2[j - 1]) ? dp[i - 1][j - 1] + 1 : max( dp[i - 1][j], dp[i][j - 1] );
        }
    }
    //  返回最终右下角的值
    return dp[m][n];
}
void solve() {
    string a, b;
    cin >> a >> b;
    cout << F(a, b);
}

试题 G: 数正方形

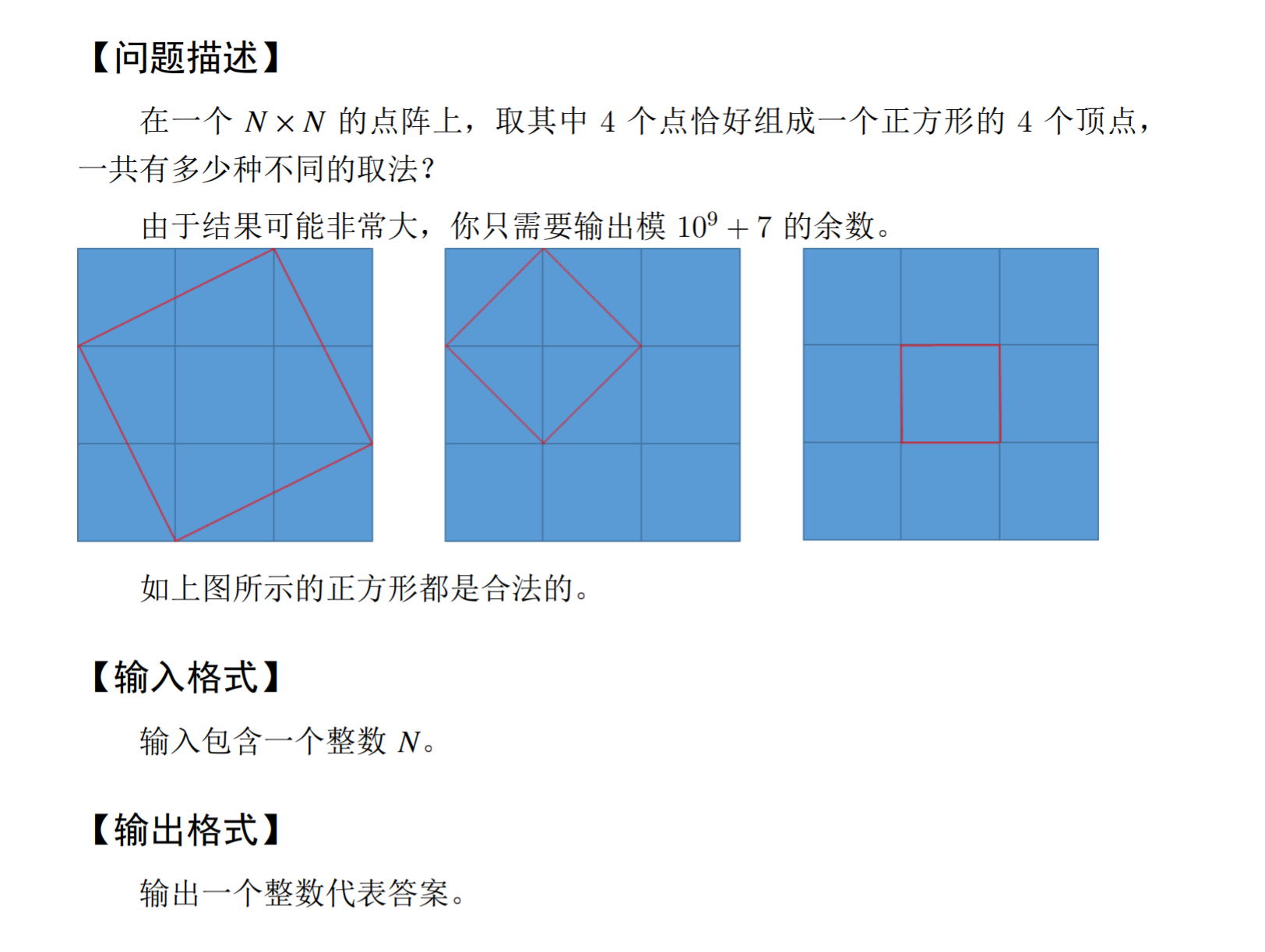
【样例输入】

4

【样例输出】

20

对于所有评测用例，\(2 ≤ N ≤ 1000000\)。

---

思路:假设N个点的边长为N-1，比如4个点的正方形边长为3，那么最小的正方形边长即为1x1

从边长1x1的正方形开始数，直到最大的正方形，即(N-1)x(N-1)，需要注意:这里对于边长不同的正方形的个数计算中，包含该大小正方形所独有的正方形

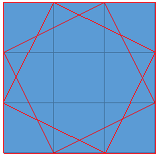
例如，上图对于边长3x3正方形的个数计算中，除了最大的3x3的正方形，还有其特有的两个正方形

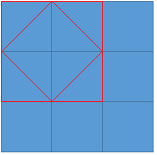
例如，上图对于边长2x2正方形的个数计算中，除了最大的2x2的正方形，还有其特有的1个正方形

对于某个nxn的正方形，其特有的正方形个数为n-1，加上该nxn的正方形，共有n个正方形

1. 边长1x1，个数(N-1)x(N-1)
2. 边长2x2，个数2x(N-2)x(N-2)
3. 边长3x3，个数3x(N-3)x(N-3)
   
   …
4. 边长(N-1)x(N-1)，个数(N-1)x1x1

最后相加

\[\notag (N-1)^2+2*(N-2)^2+3*(N-3)^2,...,+(N-1)*1^2
\]

using ll = long long;
const int mod = 1e9 + 7;
ll qpow(ll a, ll b) {
    ll ans = 1;
    for (; b; b >>= 1, a = a * a % mod)
        if (b & 1)ans = ans * a % mod;
    return ans % mod;
}
void solve() {
    ll n; cin >> n;
    ll sum = 0;
    for (int i = 0; i < n - 1; ++i)
        sum = (sum + qpow(n - (i + 1), 2) * (i + 1) % mod) % mod;
    cout << sum << '\n';
}

试题 H: 估计人数

【样例输入】

5 5 00100 11111 00100 11111 00100

【样例输出】

3

对于所有评测用例，\(1 ≤ N, M ≤ 20\)，标记为 \(1\) 的方格不超过 \(200\) 个。

待补

试题 F: 大胖子走迷宫

题目描述

小明是个大胖子，或者说是个大大胖子，如果说正常人占用 1 × 1 的面积，小明要占用 5 × 5 的面积。

由于小明太胖了，所以他行动起来很不方便。当玩一些游戏时，小明相比小伙伴就吃亏很多。

小明的朋友们制定了一个计划，帮助小明减肥，

计划的主要内容是带小明玩一些游戏，让小明在游戏中运动消耗脂肪，走迷宫是计划中的重要环节。

迷宫可以看成是一个由 n × n 个方阵组成的方阵，正常人每次占用方阵中 1 × 1 的区域，而小明要占用 5 × 5 的区域。

小明的位置定义为小明最正中的一个方格。迷宫四周都有障碍物。

为了方便小明，朋友们把迷宫的 起点 设置在了第 3 行第 3 列，终点 设置在了第 n − 2 行第 n − 2 列。

小明在时刻 0 出发，每单位时间可以向当前位置的上、下、左、右移动单位 1 的距离，也可以停留在原地不动。

小明走迷宫走得很辛苦，如果他在迷宫里面待的时间很长，由于消耗了很多脂肪，他会在时刻 k 变成一个胖子，只占用 3 × 3 的区域。

如果待的时间更长，他会在时刻 2k 变成一个正常人，只占用 1 × 1 的区域。注意，当小明变瘦时迷宫的起点和终点不变。

请问，小明最少多长时间能走到迷宫的终点。注意，小明走到终点时可能变瘦了也可能没有变瘦。

输入格式

输入的第一行包含两个整数 n, k。

接下来 n 行，每行一个由 n 个字符组成的字符串，字符为 + 表示为空地，字符为 * 表示为阻碍物。

输出格式

输出一个整数，表示答案。

样例输入

9 5+++++++++++++++++++++++++++++++++++++++++++++***+*****+++++++++++++++++++++++++++

样例输出

16

数据范围

对于 30% 的评测用例，1 ≤ n ≤ 50。

对于 60% 的评测用例，1 ≤ n ≤ 100。

对于所有评测用例，1 ≤ n ≤ 300，1 ≤ k ≤ 1000。

struct node {
    int x, y, time;
};

const int N = 310;

int n, k;
char g[N][N];
bool vis[N][N];

int dr[3] = {2, 1, 0};                                                              // 表示胖子不同时刻的半径
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};

int bfs() {
    queue<node> q;
    q.push({3, 3, 0});
    vis[3][3] = true;
    while (q.size()) {
        node t = q.front();
        q.pop();
        if (t.x == n - 2 && t.y == n - 2) return t.time;
        if (t.time / k < 2) q.push({t.x, t.y, t.time + 1});                         // 体积为 1 后，就不用原地不动了
        for (int i = 0; i < 4; i ++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            int fat = t.time / k > 2 ? 0 : dr[t.time / k];                          // 此时胖子的半径
            if (a - fat < 1 || a + fat > n || b - fat < 1 || b + fat > n) continue;
            if (vis[a][b]) continue;
            bool flag = false;                                                      // 判断胖子所占范围内是否有障碍物
            for (int j = a - fat; j <= a + fat; j ++)
                for (int k = b - fat; k <= b + fat; k ++)
                    if (g[j][k] == '*') flag = true;
            if (flag) continue;
            q.push({a, b, t.time + 1});
            vis[a][b] = true;
        }
    }
    return -1;
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i ++ ) cin >> g[i] + 1;
    cout << bfs() << endl;
    return 0;
}

试题 J: 轨道炮

【样例输入】

4
0 0 1 R
0 10 1 R
10 10 2 D
2 3 2 L

【样例输出】

3

对于所有评测用例，\(1 ≤ N ≤ 1000\)，\(−1000000 ≤ X_i , Y_i ≤ 1000000\)，\(0 ≤ V_i ≤ 1000000\)。

说明一下思路，有点像外卖优先级？

可以枚举时间，Time至 \(1\) ~ \(1000000\) 统计每个时刻行，列的最大值，最后输出即可