P3509 [POI2010] ZAB-Frog 题解

题目链接：ZAB-Frog

基于一个根据距离第 \(k\) 大的事实：

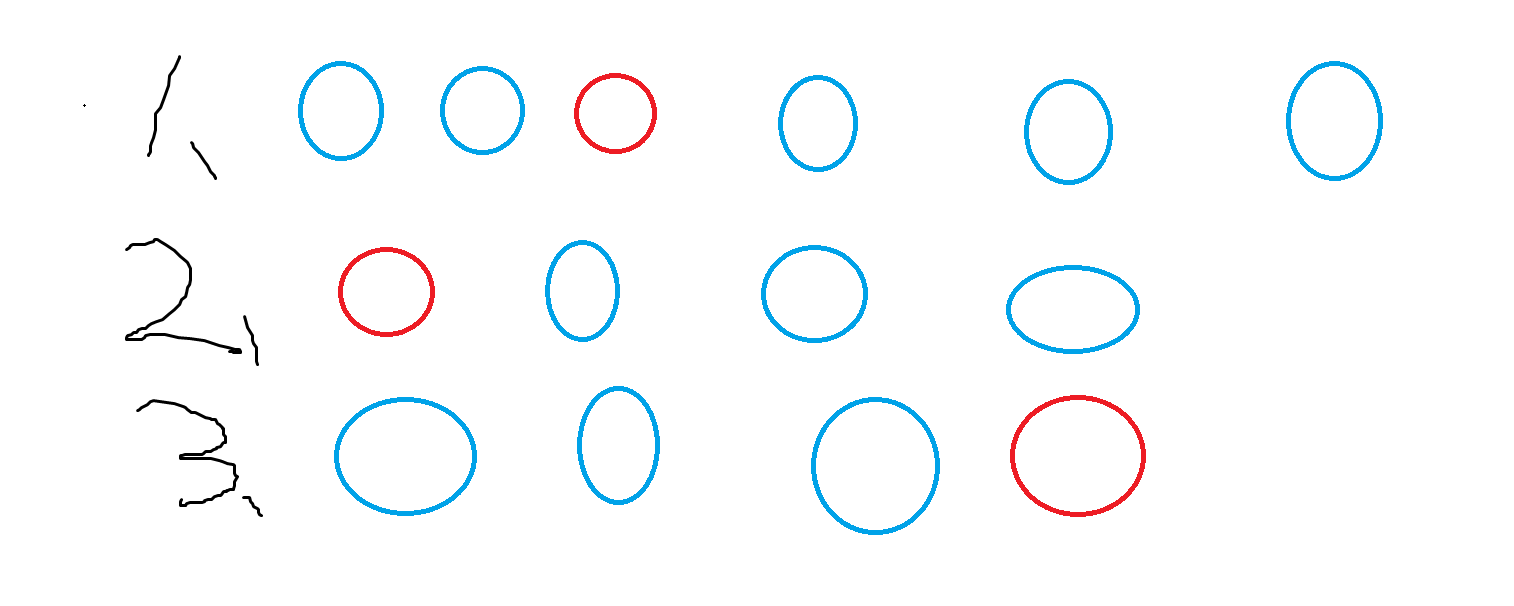
容易知道，对于红色的点而言，与它相近最近的 \(k\) 个点是连续的。而第 \(k\) 远的要么是最左侧要么是最右侧。而我们注意到原数组是升序，那么考虑红色点往右走到新的位置，这些蓝色单点整天有什么影响：

1. 左边的点离它更远了。

2. 右边原本不属于第 \(k\) 远范围内的点离它更近了。

那么当移动以后会有这么个情况，最左边开始的部分蓝色点太远了，不如最右边的新出现的蓝色的点。那么显然可以看做整体蓝色连续段往右移动了。更一般来说，将当前点与离它最近的 \(k\) 个点，放在一个窗口里，显然是连续的，而随着这个点往右移动，窗口也会往右移动，窗口大小为 \(k+1\)。那么这个窗口移动规则也很简单，新的最右边的点比最左边的点更近，就需要移除这个最左边的点，加入新的最右边的点。也就是每个点的第一次移动是很好处理出来的，滑窗处理完以后，判断左右端点谁更远就是谁是第 \(k\) 远。

考虑走 \(m\) 步，\(m\) 特别大，知道每个点走一步的情况，直接倍增预处理就能知道走 \(m\) 步的情况了。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize("Ofast,unroll-loops")
// #pragma GCC optimize(2)

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 1e6 + 10;
constexpr int T = 100;
int go[N][T];
ll a[N];
ll n, k, m;

inline void solve()
{
    cin >> n >> k >> m;
    forn(i, 1, n)cin >> a[i];
    const int MX = log2(m);
    int l = 1, r = k + 1;//包括当前点的k+1大小的滑窗
    forn(i, 1, n)
    {
        while (r + 1 <= n and a[r + 1] - a[i] < a[i] - a[l])l++, r++;//新的点更优
        go[i][0] = a[r] - a[i] > a[i] - a[l] ? r : l;//谁更远谁就是第k大,也即是第一次移动位置
    }
    forn(j, 1, MX)forn(i, 1, n)go[i][j] = go[go[i][j - 1]][j - 1];//倍增预处理
    forn(i, 1, n)
    {
        int pos = i;
        ll siz = m;
        forv(i, MX, 0)if (siz >= 1ll << i)siz -= 1ll << i, pos = go[pos][i];//倍增查找
        cout << pos << " ";
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度为 \ O(n\log{m})
\]