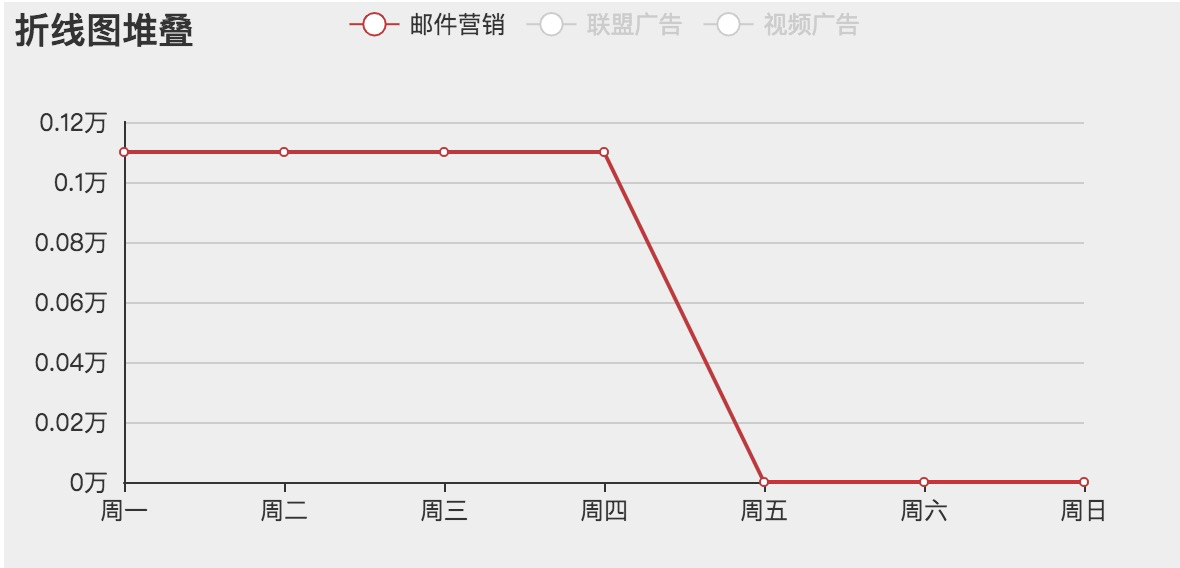
echars 实现多曲线,多Y轴,曲线单选切换,并且跟随切换指定Y轴
html代码
<!DOCTYPE html>
<html lang="en"> <head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<meta http-equiv="X-UA-Compatible" content="ie=edge">
<title>Echars|多曲线|多Y轴|Y坐标可切换</title>
</head> <body>
<script src="https://cdn.jsdelivr.net/npm/vue"></script>
<script src="https://echarts.baidu.com/examples/vendors/echarts/echarts.min.js"></script>
<div id="demo" style="width: 600px;height:300px;background:#eee"></div>
<script>
var option = {
grid:{
left:,
containLabel: true
},
tooltip: {
trigger: 'axis'
},
legend: {
selectedMode: 'single',
data: ['邮件营销', '联盟广告', '视频广告']
},
xAxis: {
type: 'category',
boundaryGap: false,
data: ['周一', '周二', '周三', '周四', '周五', '周六', '周日']
},
yAxis: [{
type: 'value',
position: 'left',
axisLabel: {
formatter: '{value}万'
},
axisTick: {
show: false
}
}, {
type: 'value',
position: 'left',
axisLabel: {
formatter: '{value}'
},
}, {
type: 'value',
position: 'left',
axisLabel: {
formatter: '{value}%'
},
}],
series: [
{
name: '邮件营销',
type: 'line',
yAxisIndex: ,
// data: [12000, 1302, 1001, 1340, 9000, 2300, 2100]
data: [0.11, 0.11, 0.11, 0.11, , , ]
},
{
name: '联盟广告',
type: 'line',
yAxisIndex: ,
data: [22.23, 182.43, 191.12, 234.43, , , ]
},
{
name: '视频广告',
type: 'line',
yAxisIndex: ,
data: [, , , , , , ]
}
]
}; var myChart = echarts.init(document.getElementById('demo'))
myChart.setOption(option) </script>
</body> </html>
echars 实现多曲线,多Y轴,曲线单选切换,并且跟随切换指定Y轴的更多相关文章
- P-R曲线及与ROC曲线区别
一.P-R曲线 P-R曲线刻画查准率和查全率之间的关系,查准率指的是在所有预测为正例的数据中,真正例所占的比例,查全率是指预测为真正例的数据占所有正例数据的比例. 即:查准率P=TP/(TP + FP ...
- 【ROC曲线】关于ROC曲线、PR曲线对于不平衡样本的不敏感性分析说引发的思考
ROC曲线 在网上有很多地方都有说ROC曲线对于正负样本比例不敏感,即正负样本比例的变化不会改变ROC曲线.但是对于PR曲线就不一样了.PR曲线会随着正负样本比例的变化而变化.但是没有一个有十分具体和 ...
- 18年春招某编程题:有三个整数X,Y,Z,要求进行若干次操作使得X,Y,Z相等
题目描述: 给定三个整数X,Y,Z,要求进行若干次操作使得X,Y,Z相等,操作有两种: 1.从X,Y,Z中选择两个数都加1. 2.从X,Y,Z中选择一个数加2. 求最少需要多少次操作. 题目思路: 1 ...
- 函数的光滑化或正则化 卷积 应用 两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积
http://graphics.stanford.edu/courses/cs178/applets/convolution.html Convolution is an operation on t ...
- C# 历史曲线控件 基于时间的曲线控件 可交互的高级曲线控件 HslControls曲线控件使用教程
本篇博客主要对 HslControls 中的曲线控件做一个详细的教程说明,大家可以根据下面的教程开发出高质量的曲线控件 Prepare 先从nuget下载到组件,然后就可以使用组件里的各种组件信息了. ...
- [osg][原]osg的坐标系:使用右手法则Y轴向前、X向、右Z向上。camare的默认姿态:向下看(Z轴负向),头向前(Y轴正向)
参考:http://blog.csdn.net/tmljs1988/article/details/7561887 图中上半边为opengl坐标系,下半边的osg坐标系: osg::Camare的默认 ...
- 如果int x=20, y=5,则语句System.out.println(x+y +""+(x+y)+y); 的输出结果是()
答案是25255 小括号优先级高,所以先算小括号内的x+y=25 然后再算前面的x+y=25 但是中间有个空的字符串,java会把这个空字符串后面的都当成字符串看待,所以结果是25255
- 怎样理解在函数中声明var x = y = 1后调用函数时, x是局部变量, y是全局变量
下面这段代码在执行的时候, 打印的结果是1, Error: undefined; function fn() { var x = y = 1; } fn(); console.log(y); // 1 ...
- 线段树 区间更新(更新区间[x,y]的值,再求任意区间[x,y]的和)
#1078 : 线段树的区间修改 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 对于小Ho表现出的对线段树的理解,小Hi表示挺满意的,但是满意就够了么?于是小Hi将问题 ...
随机推荐
- 第九周周四计划&&周三总结
今天由于自己的原因进度不是很大,今天整理了一下全网关联的思路流程(个人可能就是那种没自信,在思路不知道对不对的情况下不敢下手那种渣渣),和之前的一个学长讨论了一下大概思路流程,如下: (1)使用LDA ...
- JAVA多线程间隔时间段执行方法
import java.util.Date; import java.util.Timer; import java.util.TimerTask; public class ManyProject ...
- DRF--介绍和安装
前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示,前端与后端的耦合度很高.这种应用模式比较适合纯网页应用,但是当后端对接 ...
- 【ECNU3510】燃烧吧,室友!(模拟)
点此看题面 大致题意: 给你一个只含\(C,H,O\)的化学式,问需要几\(mol\)的氧气才能使其完全燃烧成\(CO_2\)和\(H_2O\). 模拟+化学 首先,我们模拟求出化学式中\(C,H,O ...
- QTreeWidgetItem清空子节点
下面列出,xxbs遇到的注意点儿: 1. QTreeWidget::collapseAll(); //xxbs::先折叠所有根项. 如果某个根是展开的,先删除根的子项再折叠,展开的凸显状态角色无法清除 ...
- tomcat参数java_opts调整
启动文件修改 在windows环境下,tomcat下的~/bin/catalina.bat文件,在文件头部加入: set "JAVA_OPTS=%JAVA_OPTS% -server -Xm ...
- Java-100天知识进阶-JVM内存-知识铺(三)
知识铺: 致力于打造轻知识点,持续更新每次的知识点较少,阅读不累.不占太多时间,不停的来唤醒你记忆深处的知识点. Java内存模型(JMM) JVM内存模式是JVM的内存分区 Java内存模式是一种虚 ...
- Python 文件readlines()方法
原文连接:https://www.runoob.com/python/file-readlines.html readlines()方法用于读取所有行(直到结束符EOF)并返回列表,该列表可以由pyt ...
- 分享windows 10 下部署 elasticsearch 和 logstash (二)
接上一篇,es部署很简单,很快就弄好了. 但是还是有很多不玩美. 比如说:主机是本地的IP或机器名,端口是固定的9200. 而且是只有一个节点,我要在一台机器上部署多个节点呢. 经过一段时间的摸索,做 ...
- C# winform 获取鼠标点击位置
说明:该篇随笔的代码内容并非出自本人,是在其他网站搜寻的,出处已经不记得了,本次随笔只为记录,目的帮助自己,帮助他人. 实现的原理也不做多的赘述,直接上代码. 第一个类是需要用到的Windows AP ...
