转载：奇异值分解(SVD) --- 线性变换几何意义（上）

本文转载自他人：

PS：一直以来对SVD分解似懂非懂，此文为译文，原文以细致的分析+大量的可视化图形演示了SVD的几何意义。能在有限的篇幅把这个问题讲解的如此清晰，实属不易。原文举了一个简单的图像处理问题，简单形象，真心希望路过的各路朋友能从不同的角度阐述下自己对SVD实际意义的理解，比如 个性化推荐中应用了SVD，文本以及Web挖掘的时候也经常会用到SVD。

原文：We recommend a singular value decomposition

简介

SVD实际上是数学专业内容，但它现在已经渗入到不同的领域中。SVD的过程不是很好理解，因为它不够直观，但它对矩阵分解的效果却非常好。比如，Netflix（一个提供在线电影租赁的公司）曾经就悬赏100万美金，如果谁能提高它的电影推荐系统评分预测准确率提高10%的话。令人惊讶的是，这个目标充满了挑战，来自世界各地的团队运用了各种不同的技术。最终的获胜队伍"BellKor's Pragmatic Chaos"采用的核心算法就是基于SVD。

SVD提供了一种非常便捷的矩阵分解方式，能够发现数据中十分有意思的潜在模式。在这篇文章中，我们将会提供对SVD几何上的理解和一些简单的应用实例。

线性变换的几何意义(The geometry of linear transformations)

让我们来看一些简单的线性变换例子，以 2 X 2 的线性变换矩阵为例，首先来看一个较为特殊的，对角矩阵：

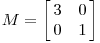
从几何上讲，M 是将二维平面上的点(x,y)经过线性变换到另外一个点的变换矩阵，如下图所示

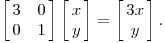
变换的效果如下图所示，变换后的平面仅仅是沿 X 水平方面进行了拉伸3倍，垂直方向是并没有发生变化。

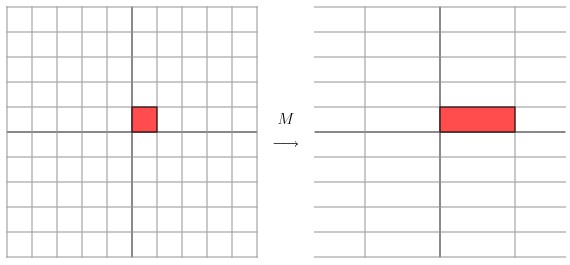
现在看下矩阵

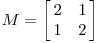
这个矩阵产生的变换效果如下图所示

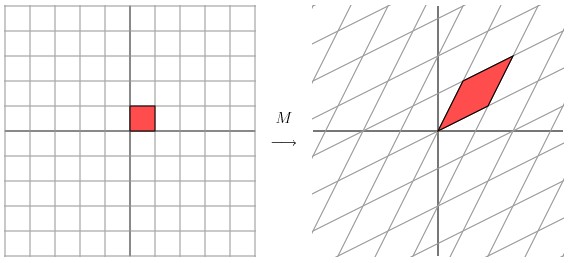
这种变换效果看起来非常的奇怪，在实际环境下很难描述出来变换的规律 ( 这里应该是指无法清晰辨识出旋转的角度，拉伸的倍数之类的信息)。还是基于上面的对称矩阵，假设我们把左边的平面旋转45度角，然后再进行矩阵 M 的线性变换，效果如下图所示：

看起来是不是有点熟悉？ 对的，经过 M 线性变换后，跟前面的对角矩阵的功能是相同的，都是将网格沿着一个方向拉伸了3倍。

这里的 M 是一个特例，因为它是对称的。非特殊的就是我们在实际应用中经常遇见一些 非对称的，非方阵的矩阵。如上图所示，如果我们有一个 2 X 2 的对称矩阵 M 的话，我们先将网格平面旋转一定的角度，M 的变换效果就是在两个维度上进行拉伸变换了。

用更加数学的方式进行表示的话，给定一个对称矩阵 M ，我们可以找到一些相互正交 V_i ，满足 MV_i 就是沿着 V_i 方向的拉伸变换，公式如下：

Mv_i = λ_iv_i

这里的 λ_i 是拉伸尺度(scalar)。从几何上看，M 对向量 V_i 进行了拉伸，映射变换。V_i 称作矩阵 M 的特征向量(eigenvector)， λ_i 称作为矩阵 M 特征值(eigenvalue)。这里有一个非常重要的定理，对称矩阵 M 的特征向量是相互正交的。

如果我们用这些特征向量对网格平面进行线性变换的话，再通过 M 矩阵对网格平面进行线性换的效果跟对 M 矩阵的特征向量进行线性变换的效果是一样的。

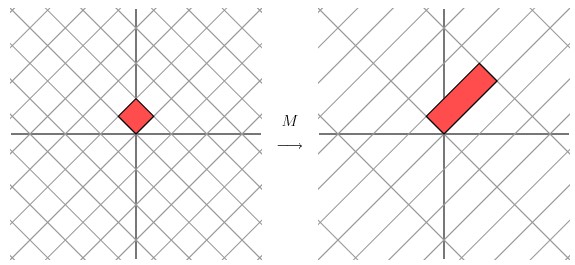
对于更为普通的矩阵而言，我们该怎么做才能让一个原来就是相互垂直的网格平面(orthogonal grid), 线性变换成另外一个网格平面同样垂直呢？PS：这里的垂直如图所示，就是两根交错的线条是垂直的。

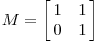
经过上述矩阵变换以后的效果如图

从图中可以看出，并没有达到我们想要的效果。我们把网格平面旋转 30 度角的话，然后再进行同样的线性变换以后的效果，如下图所示

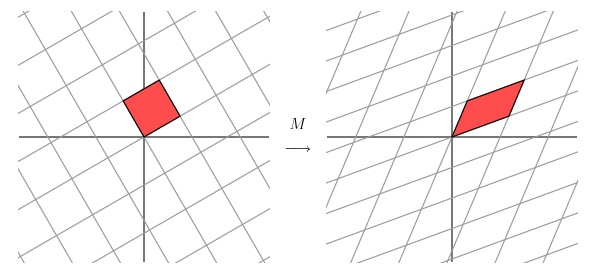
让我们来看下网格平面旋转60度角的时候的效果。

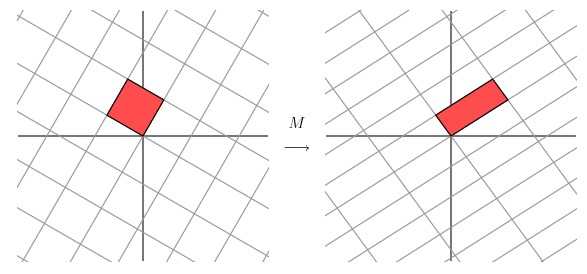
嗯嗯，这个看起来挺不错的样子。如果在精确一点的话，应该把网格平面旋转 58.28 度才能达到理想的效果。