.NET中常见的加解密方式

　　在互联网普及的初期，人们更关注单纯的连接性，以不受任何限制地建立互联网为最终目的。正如事情都具有两面性，互联网的便捷性给人们带来了负面问题，计算机病毒的侵害、信息泄露、网络欺诈等利用互联网的犯罪行为日益增多。而对通讯过程中进行加密很大抑制这种情况发生，下面是主要介绍.NET中常用的几种加密及解密方式。

　　.NET中有三种常见的加密方式：不可逆加密、对称可逆加密、非对称可逆加密。

　　不可逆加密

　　不可逆加密算法的特征是加密过程中不需要使用密钥，输入明文后由系统直接经过加密算法处理成密文，这种加密后的数据是无法被解密的，只有重新输入明文，并再次经过同样不可逆的加密算法处理，得到相同的加密密文并被系统重新识别后，才能真正解密。

　　MD5加密是现有主流不可逆加密方式。MD5（单向散列算法）的全称是Message-Digest Algorithm 5（信息-摘要算法），经MD2、MD3和MD4发展而来。

　　MD5的加密算法是公开的，无论哪种编程语言，同样的字符串加密后的结果都是一样的，以下是用.NET实现的MD5加密类：

public class MD5Encrypt
    {
        #region MD5
        /// <summary>
        /// </summary>
        /// <param name="source">待加密字串</param>
        /// <param name="length">16或32值之一,其它则采用.net默认MD5加密算法</param>
        /// <returns>加密后的字串</returns>
        public static string Encrypt(string source, int length = )//默认参数
        {
            if (string.IsNullOrEmpty(source)) return string.Empty;
            HashAlgorithm provider = CryptoConfig.CreateFromName("MD5") as HashAlgorithm;
            byte[] bytes = Encoding.UTF8.GetBytes(source);
            byte[] hashValue = provider.ComputeHash(bytes);
            StringBuilder sb = new StringBuilder();
            switch (length)
            {
                case :
                    for (int i = ; i < ; i++)
                    {
                        sb.Append(hashValue[i].ToString("x2"));
                    }
                    break;
                case :
                    for (int i = ; i < ; i++)
                    {
                        sb.Append(hashValue[i].ToString("x2"));
                    }
                    break;
                default:
                    for (int i = ; i < hashValue.Length; i++)
                    {
                        sb.Append(hashValue[i].ToString("x2"));
                    }
                    break;
            }
            return sb.ToString();
        }
        #endregion MD5

        #region MD5摘要
        /// <summary>
        /// 获取文件的MD5摘要
        /// </summary>
        /// <param name="fileName"></param>
        /// <returns></returns>
        public static string AbstractFile(string fileName)
        {
            using (FileStream file = new FileStream(fileName, FileMode.Open))
            {
                return AbstractFile(file);
            }
        }

        /// <summary>
        /// 根据stream获取文件摘要
        /// </summary>
        /// <param name="stream"></param>
        /// <returns></returns>
        public static string AbstractFile(Stream stream)
        {
            MD5 md5 = new MD5CryptoServiceProvider();
            byte[] retVal = md5.ComputeHash(stream);

            StringBuilder sb = new StringBuilder();
            for (int i = ; i < retVal.Length; i++)
            {
                sb.Append(retVal[i].ToString("x2"));
            }
            return sb.ToString();
        }
        #endregion
    }

　　MD5不仅可对字段串进行加密，也可以对文件进行加密。

　   用途：

　　1.防止看到明文：可以用于一些不需要原文的验证方式。像一些用户密码直接暴露明文保存在数据库很容易被人获取到，而MD5加密正好符合这个场景，直接用MD5加密后的密文当做密码，当用户登录的时候可输入原文，后台只需验证MD5加密后的密文是否相符即可，也可以在这个基础上对原文进行加盐、双MD5进行加密。

　　2.防篡改：MD5除了可以对字符串进行加密外，还可以对文件进行加密（文件流），加密后产生的MD5可以验证这个文件的唯一性。

　　　　急速秒传：在此基础上，用户第一次上传文件时候保存文件，并将此文件生成一个MD5摘要，当别的用户再次上传此文件时，会将此文件的MD5与数据库进行对照，若发现有相同的MD5摘要，则将文件路径指向相同此文件，并直接告诉用户上传成功。

　　　　文件下载：官方发布文件包的时候给一个md5摘要，安装的时候首先检查下摘要

　　3.防止抵赖：由于MD5加密后的结果是唯一的，由此产生一些第三方权威认证机构（CA）可对文件进行认证，后返回认证的MD5摘要。

　　

对称可逆加密

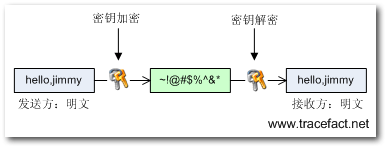
　　对称加密的思路非常简单，就是含有一个称为密钥的东西，在消息发送前使用密钥对消息进行加密，在对方收到消息之后，使用相同的密钥进行解密。根据密钥来产生加密后的消息（密文）的这一加工过程，由加密算法来完成，加密算法通常是公开的。它的流程如下：

1. 发送方使用密钥对消息进行加密。
2. 接收方使用同样的密钥对消息进行解密。

　　可以使用下面一副图来表示：

以下是.NET对DES加密算法的封装：

public class DesEncrypt
    {
        private static byte[] _rgbKey = ASCIIEncoding.ASCII.GetBytes(Constant.DesKey.Substring(, ));
        private static byte[] _rgbIV = ASCIIEncoding.ASCII.GetBytes(Constant.DesKey.Insert(, "w").Substring(, ));

        /// <summary>
        /// DES 加密
        /// </summary>
        /// <param name="text">需要加密的值</param>
        /// <returns>加密后的结果</returns>
        public static string Encrypt(string text)
        {
            DESCryptoServiceProvider dsp = new DESCryptoServiceProvider();
            using (MemoryStream memStream = new MemoryStream())
            {
                CryptoStream crypStream = new CryptoStream(memStream, dsp.CreateEncryptor(_rgbKey, _rgbIV), CryptoStreamMode.Write);
                StreamWriter sWriter = new StreamWriter(crypStream);
                sWriter.Write(text);
                sWriter.Flush();
                crypStream.FlushFinalBlock();
                memStream.Flush();
                return Convert.ToBase64String(memStream.GetBuffer(), , (int)memStream.Length);
            }
        }

        /// <summary>
        /// DES解密
        /// </summary>
        /// <param name="encryptText"></param>
        /// <returns>解密后的结果</returns>
        public static string Decrypt(string encryptText)
        {
            DESCryptoServiceProvider dsp = new DESCryptoServiceProvider();
            byte[] buffer = Convert.FromBase64String(encryptText);

            using (MemoryStream memStream = new MemoryStream())
            {
                CryptoStream crypStream = new CryptoStream(memStream, dsp.CreateDecryptor(_rgbKey, _rgbIV), CryptoStreamMode.Write);
                crypStream.Write(buffer, , buffer.Length);
                crypStream.FlushFinalBlock();
                return ASCIIEncoding.UTF8.GetString(memStream.ToArray());
            }
        }
    }

对称加密算法的优点是速度快，但是也有个最大的缺点，秘钥的存储问题，用对称加密进行网络通讯，那就必须双方都持有同一个秘钥，这就是需要将秘钥共享，一旦秘钥泄露也就毫无加密可言。

　　非对称可逆加密

　　非对称可逆加密算法可随机生一组秘钥（.NET已经封装在RSACryptoServiceProvider中），其中一个叫加密钥，一个叫解密钥，可通过加密钥进行加密得到密文，再通过解密要进行解密。

　　公钥：对外公布的加密钥或者解密钥。

　　私钥：不对外公布的加密钥或者解密钥。

　　使用非对称加密往往会向外界提供一个公钥，自身保存一个私钥。

　　以下是.NET实现的RSA非对称可逆加密：

　　

 public class RsaEncrypt
     {
         /// <summary>
         /// 获取加密/解密对
         /// 给你一个，是无法推算出另外一个的
         ///
         /// Encrypt   Decrypt
         /// </summary>
         /// <returns>Encrypt   Decrypt</returns>
         public static KeyValuePair<string, string> GetKeyPair()
         {
             RSACryptoServiceProvider RSA = new RSACryptoServiceProvider();
             string publicKey = RSA.ToXmlString(false);
             string privateKey = RSA.ToXmlString(true);
             return new KeyValuePair<string, string>(publicKey, privateKey);
         }

         /// <summary>
         /// 加密：内容+加密key
         /// </summary>
         /// <param name="content"></param>
         /// <param name="encryptKey">加密key</param>
         /// <returns></returns>
         public static string Encrypt(string content, string encryptKey)
         {
             RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();
             rsa.FromXmlString(encryptKey);
             UnicodeEncoding ByteConverter = new UnicodeEncoding();
             byte[] DataToEncrypt = ByteConverter.GetBytes(content);
             byte[] resultBytes = rsa.Encrypt(DataToEncrypt, false);
             return Convert.ToBase64String(resultBytes);
         }

         /// <summary>
         /// 解密  内容+解密key
         /// </summary>
         /// <param name="content"></param>
         /// <param name="decryptKey">解密key</param>
         /// <returns></returns>
         public static string Decrypt(string content, string decryptKey)
         {
             byte[] dataToDecrypt = Convert.FromBase64String(content);
             RSACryptoServiceProvider RSA = new RSACryptoServiceProvider();
             RSA.FromXmlString(decryptKey);
             byte[] resultBytes = RSA.Decrypt(dataToDecrypt, false);
             UnicodeEncoding ByteConverter = new UnicodeEncoding();
             return ByteConverter.GetString(resultBytes);
         }

         /// <summary>
         /// 可以合并在一起的，，每次产生一组新的密钥
         /// </summary>
         /// <param name="content"></param>
         /// <param name="encryptKey">加密key</param>
         /// <param name="decryptKey">解密key</param>
         /// <returns>加密后结果</returns>
         private static string Encrypt(string content, out string publicKey, out string privateKey)
         {
             RSACryptoServiceProvider rsaProvider = new RSACryptoServiceProvider();
             publicKey = rsaProvider.ToXmlString(false);
             privateKey = rsaProvider.ToXmlString(true);

             UnicodeEncoding ByteConverter = new UnicodeEncoding();
             byte[] DataToEncrypt = ByteConverter.GetBytes(content);
             byte[] resultBytes = rsaProvider.Encrypt(DataToEncrypt, false);
             return Convert.ToBase64String(resultBytes);
         }
     }

　　非对称可逆加密产生的加解密钥是不法互推的，就是说你拿到解密钥或者加密钥你是无法推算出另一个密钥的，这是跟对称加密最大的不同。