51NOD 1833 环

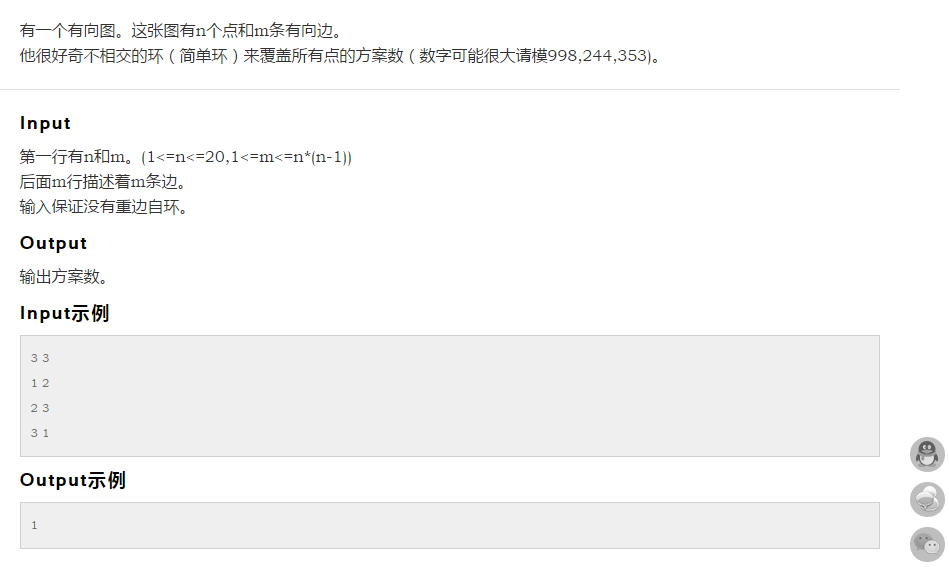
考虑一下简单环覆盖这个图的意义，其实就是找出原序列的所有排列，满足所有<i,a[i]>都是原图中的一条有向边。 因为一个置换就是由很多简单环构成的。

于是我们可以设 f[i][S] 为考虑了前i个点的出边，且有入度的点集为S的方案数。 直接dp不难发现复杂度是 O(n^2 * 2^n)，正好会T掉2333.

但是进一步发现，因为每个点都要匹配另一个点，也就是说 S 集合中1的个数必须和i一样，所以预处理一下 bitcount 就可以把复杂度降到 O(n * 2^n)了。

#include<bits/stdc++.h>
#define ll long long
const int ha=998244353;
const int maxn=1100005;
int f[maxn],n,m,ci[25],BT[maxn];
bool G[25][25];
inline void add(int &x,int y){ x+=y; if(x>+ha) x-=ha;}

inline void dp(){
	f[0]=1,BT[0]=0;
	for(int i=1;i<ci[n];i++) BT[i]=BT[i^(i&-i)]+1;
	for(int i=0;i<n;i++)
	    for(int S=ci[n]-1;S>=0;S--) if(f[S]&&BT[S]==i)
	        for(int j=0;j<n;j++) if(!(ci[j]&S)&&G[i][j]) add(f[S|ci[j]],f[S]);
}

int main(){
	ci[0]=1;
	for(int i=1;i<=20;i++) ci[i]=ci[i-1]<<1;
	int uu,vv;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++) scanf("%d%d",&uu,&vv),G[uu-1][vv-1]=1;
	dp();
	printf("%d\n",f[ci[n]-1]);
	return 0;
}