SP14932 LCA - Lowest Common Ancestor

Description:

一棵树是一个简单无向图，图中任意两个节点仅被一条边连接，所有连通无环无向图都是一棵树。\(-Wikipedia\)

最近公共祖先（\(LCA\)）是……（此处省去对\(LCA\)的描述），你的任务是对一棵给定的树\(T\)以及上面的两个节点\(u,v\)求出他们的\(LCA\)。

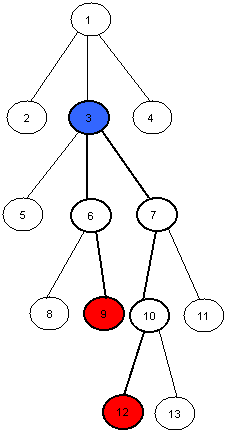
例如图中9和12号节点的LCA为3号节点

Input:

输入的第一行为数据组数\(T\)，对于每组数据，第一行为一个整数\(N(1\leq N\leq1000)\)，节点编号从\(1\)到\(N\)，接下来的\(N\)行里每一行开头有一个数字\(M(0\leq M\leq999)\)，\(M\)为第\(i\)个节点的子节点数量，接下来有\(M\)个数表示第\(i\)个节点的子节点编号。下面一行会有一个整数\(Q(1\leq Q\leq1000)\)，接下来的\(Q\)行每行有两个数\(u,v\)，输出节点\(u,v\)在给定树中的\(LCA\)。

输入数据保证只有一个根节点并且没有环。

Output:

对于每一组数据输出\(Q+1\)行，第一行格式为\("Case i:"\)（没有双引号），\(i\)表示当前数据是第几组，接下来的\(Q\)行每一行一个整数表示一对节点\(u,v\)的\(LCA\)。

Sample Input:

1
7
3 2 3 4
0
3 5 6 7
0
0
0
0
2
5 7
2 7

Sample Output:

Case 1:
3
1

\(Translated by @_yxl_g\)l_

思路：一道求\(LCA\)的板子题，根据题目给出的每个点的孩子建边然后找出根结点，直接\(dfs\)求出深度后跑\(LCA\)就可以了。

代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 1007
using namespace std;
int t,q,rt,tim,f[maxn][22],n,m,head[maxn],d[maxn],num;
bool vis[maxn];
struct node {
  int v,nxt;
}e[maxn<<1];
inline void ct(int u, int v) {
  e[++num].v=v;
  e[num].nxt=head[u];
  head[u]=num;
}
void dfs(int u, int fa) {
  for(int i=head[u];i;i=e[i].nxt) {
    int v=e[i].v;
    if(v!=fa) {
      f[v][0]=u;
      d[v]=d[u]+1;
      dfs(v,u);
    }
  }
}
inline int lca(int a, int b) {
  if(d[a]>d[b]) swap(a,b);
  for(int i=20;i>=0;--i)
  if(d[a]<=d[b]-(1<<i)) b=f[b][i];
  if(a==b) return a;
  for(int i=20;i>=0;--i)
  if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
  return f[a][0];
}
int main() {
  scanf("%d",&t);
  while(t--) {
    ++tim;
    memset(f,0,sizeof(f));
    memset(d,0,sizeof(d));
    memset(head,0,sizeof(head));
    memset(vis,0,sizeof(vis));
    num=0;
    scanf("%d",&n);
    for(int i=1,m;i<=n;++i) {
      scanf("%d",&m);
      for(int j=1,v;j<=m;++j) {
        scanf("%d",&v);
        ct(i,v);ct(v,i);
        vis[v]=1;
      }
    }
    for(int i=1;i<=n;++i) if(!vis[i]) rt=i;
    dfs(rt,0);
    for(int j=1;j<=20;++j)
    for(int i=1;i<=n;++i)
    f[i][j]=f[f[i][j-1]][j-1];
    scanf("%d",&q);
    printf("Case %d:\n",tim);
    for(int i=1,u,v;i<=q;++i) {
      scanf("%d%d",&u,&v);
      printf("%d\n",lca(u,v));
    }
  }
  return 0;
}