非负矩阵分解（NMF）原理及算法实现

一、矩阵分解回想

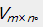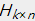矩阵分解是指将一个矩阵分解成两个或者多个矩阵的乘积。对于上述的用户-商品（评分矩阵），记为能够将其分解为两个或者多个矩阵的乘积，如果分解成两个矩阵和 。我们要使得矩阵和 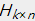的乘积能够还原原始的矩阵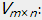

当中，矩阵表示的是m个用户于k个主题之间的关系，而矩阵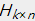表示的是k个主题与n个商品之间的关系

通常在用户对商品进行打分的过程中，打分是非负的，这就要求：

这便是非负矩阵分解（NMF）的来源。

二、非负矩阵分解

2.1、非负矩阵分解的形式化定义

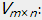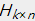上面介绍了非负矩阵分解的基本含义。简单来讲，非负矩阵分解是在矩阵分解的基础上对分解完毕的矩阵加上非负的限制条件。即对于用户-商品矩阵找到两个矩阵和 ，使得：

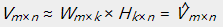
同一时候要求：

2.2、损失函数

为了能够定量的比较矩阵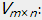和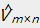的近似程度，提出了两种损失函数的定义方式：
欧几里得距离：

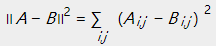
KL散度：

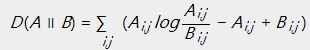
在KL散度的定义中，。当且仅当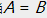时取得等号。

当定义好损失函数后，须要求解的问题就变成了例如以下的形式，相应于不同的损失函数：

求解例如以下的最小化问题：

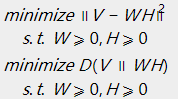
2.3、优化问题的求解

乘法更新规则，详细操作例如以下：

对于欧几里得距离的损失函数：

对于KL散度的损失函数：

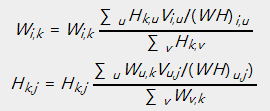
上述的乘法规则主要是为了在计算的过程中保证非负，而基于梯度下降的方法中，加减运算无法保证非负。事实上上述的惩罚更新规则与梯度下降的算法是等价的。以下以平方距离为损失函数说明上述过程的等价性：

平方损失函数能够写成：

使用损失函数对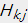求偏导数：

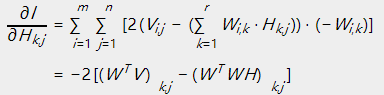
依照梯度下降法的思路：

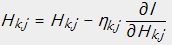
即为：

令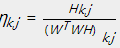，即能够得到上述的乘法更新规则的形式。

2.4、非负矩阵分解的实现

 from numpy import *
 from pylab import *
 from numpy import *

 def load_data(file_path):
     f = open(file_path)
     V = []
     for line in f.readlines():
         lines = line.strip().split("\t")
         data = []
         for x in lines:
             data.append(float(x))
         V.append(data)
     return mat(V)

 def train(V, r, k, e):
     m, n = shape(V)
     #先随机给定一个W、H，保证矩阵的大小
     W = mat(random.random((m, r)))
     H = mat(random.random((r, n)))
 #K为迭代次数
     for x in range(k):
         #error
         V_pre = W * H
         E = V - V_pre
         #print E
         err = 0.0
         for i in range(m):
             for j in range(n):
                 err += E[i,j] * E[i,j]
         print(err)
         data.append(err)

         if err < e:
             break
 #权值更新
         a = W.T * V
         b = W.T * W * H
         #c = V * H.T
         #d = W * H * H.T
         for i_1 in range(r):
             for j_1 in range(n):
                 if b[i_1,j_1] != 0:
                     H[i_1,j_1] = H[i_1,j_1] * a[i_1,j_1] / b[i_1,j_1]

         c = V * H.T
         d = W * H * H.T
         for i_2 in range(m):
             for j_2 in range(r):
                 if d[i_2, j_2] != 0:
                     W[i_2,j_2] = W[i_2,j_2] * c[i_2,j_2] / d[i_2, j_2]

     return W,H,data

 if __name__ == "__main__":
     #file_path = "./data_nmf"
     # file_path = "./data1"
     data = []
     # V = load_data(file_path)
     V=[[5,3,2,1],[4,2,2,1,],[1,1,2,5],[1,2,2,4],[2,1,5,4]]
     W, H ,error= train(V, 2, 100, 1e-5 )
     print (V)
     print (W)
     print (H)
     print (W * H)
     n = len(error)
     x = range(n)
     plot(x, error, color='r', linewidth=3)
     plt.title('Convergence curve')
     plt.xlabel('generation')
     plt.ylabel('loss')
     show()

这里需要注意训练时r值的选择：r可以表示和主题数或者你想要的到的特征数

K值的选择：k表示训练的次数，设置的越大模型的拟合效果越好，但是具体设置多少，要根据性价比看，看误差曲线的变化