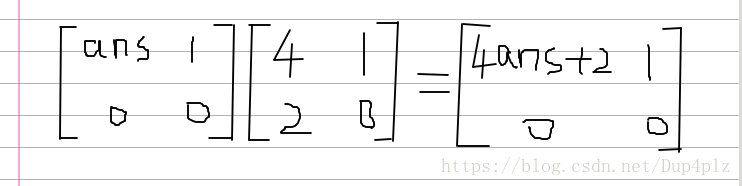HDU - 4990 Reading comprehension 【矩阵快速幂】
题目链接
http://acm.hdu.edu.cn/showproblem.php?pid=4990
题意
初始的ans = 0
给出 n, m
for i in 1 -> n
如果 i 为奇数
ans = (ans * 2 + 1) % m
反之
ans = ans * 2 % m
思路
如果我们只计算 偶数项 那么递推公式就是
ans[n] = 4 * ans[n - 2] + 2
如果 n 是偶数 那么刚好 就按这个公式推 第 n / 2 项
如果 n 是奇数 那么就是 第 【 n / 2 项 】 * 2 + 1
可以推知的矩阵为
然后矩阵快速幂
AC代码
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>
#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back
using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;
const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const int maxn = 1e2 + 5;
//const int MOD = 1e4;
int MOD;
struct Matrix
{
ll a[2][2];
Matrix () {}
Matrix operator * (Matrix const &b)const
{
Matrix res;
CLR(res.a, 0);
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++)
for (int k = 0; k < 2; k++)
res.a[i][j] = (res.a[i][j] + this->a[i][k] * b.a[k][j]) % MOD;
return res;
}
};
Matrix pow_mod(Matrix base, int n)
{
Matrix ans;
CLR(ans.a, 0);
ans.a[0][1] = 1;
while (n > 0)
{
if (n & 1)
ans = ans * base;
base = base * base;
n >>= 1;
}
return ans;
}
int main()
{
Matrix base;
base.a[0][0] = 4;
base.a[0][1] = 0;
base.a[1][0] = 2;
base.a[1][1] = 1;
int n;
while (~scanf("%d%d", &n, &MOD))
{
Matrix ans = pow_mod(base, n / 2);
if (n & 1)
printf("%lld\n", (ans.a[0][0] * 2 + 1) % MOD);
else
printf("%lld\n", ans.a[0][0] % MOD);
}
}
HDU - 4990 Reading comprehension 【矩阵快速幂】的更多相关文章
- HDU 4990 Reading comprehension 矩阵快速幂
题意: 给出一个序列, \(f_n=\left\{\begin{matrix} 2f_{n-1}+1, n \, mod \, 2=1\\ 2f_{n-1}, n \, mod \, 2=0 \end ...
- hdu 4990 Reading comprehension 二分 + 快速幂
Description Read the program below carefully then answer the question. #pragma comment(linker, " ...
- hdu4990 Reading comprehension 矩阵快速幂
Read the program below carefully then answer the question.#pragma comment(linker, "/STACK:10240 ...
- HDU.1575 Tr A ( 矩阵快速幂)
HDU.1575 Tr A ( 矩阵快速幂) 点我挑战题目 题意分析 直接求矩阵A^K的结果,然后计算正对角线,即左上到右下对角线的和,结果模9973后输出即可. 由于此题矩阵直接给出的,题目比较裸. ...
- hdu 3117 Fibonacci Numbers 矩阵快速幂+公式
斐波那契数列后四位可以用快速幂取模(模10000)算出.前四位要用公式推 HDU 3117 Fibonacci Numbers(矩阵快速幂+公式) f(n)=(((1+√5)/2)^n+((1-√5) ...
- HDU 4990 Reading comprehension 简单矩阵快速幂
Problem Description Read the program below carefully then answer the question.#pragma comment(linker ...
- HDU 2842 (递推+矩阵快速幂)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2842 题目大意:棒子上套环.第i个环能拿下的条件是:第i-1个环在棒子上,前i-2个环不在棒子上.每个 ...
- hdu 2604 Queuing(矩阵快速幂乘法)
Problem Description Queues and Priority Queues are data structures which are known to most computer ...
- HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5950 Farmer John likes to play mathematics games with ...
随机推荐
- Linux 双网卡 不同网段 网络互通
环境如下: 现状:一台linux主机上有两个网卡eth0 和eth1 ,机器能访问192网的服务资源,但不能访问10网段的资源. 要求:linux能通过eth1访问10网段的资源 路由: 网卡: 操作 ...
- mac python 切换系统默认版本
1 找到所安装python路径/usr/local/Cellar/python/2.7.13/bin2 vim ~/.bash_profile 3 添加如下代码: PATH="/usr/lo ...
- goreplay使用
最新版的发布公告:https://leonsbox.com/goreplay-v0-16-and-4th-anniversary-5408b1fd72e0 主要提到:中间件.报文解压.从kafka读取 ...
- tomcat下配置https方式
[本地HTTPS]①.<Connector SSLEnabled="true" clientAuth="false" keystoreFile=" ...
- java wait(),notify(),notifyAll()的理解
这个三个函数来自Object类,众所周知它们是用于多线程同步的.然而,有个问题却一直没搞清楚,即notify()函数到底通知谁?<Thinking in JAVA>中有这么一句话,当not ...
- springboot + mybatis配置多数据源示例
转:http://www.jb51.net/article/107223.htm 在实际开发中,我们一个项目可能会用到多个数据库,通常一个数据库对应一个数据源. 代码结构: 简要原理: 1)Datab ...
- Smart Battery Specification Revision 1.1
1.SBS Specifications 2.System Management Bus (SMBus) Specification
- Redis(九):使用RedisTemplate访问Redis数据结构API大全
RedisTemplate介绍 spring封装了RedisTemplate对象来进行对redis的各种操作,它支持所有的 redis 原生的api. RedisTemplate在spring代码中的 ...
- 删除反复行SQL举例
删除反复行SQL实验简单举例 说明:实验按顺序进行.前后存在关联性.阅读时请注意.打开文件夹更便于查看. 构造实验环境: SQL> select count(*) from emp; COU ...
- com.opensymphony.xwork2.ognl.OgnlValueStack - Error setting expression 'customer.applyRate' with value '[Ljava.lang.String;@7d3fae2c'
出错的3个最可能的原因:我是第二种错误 1.action配置错误 <action name="doCreateMeetingInfo" class="meeting ...