蓝桥杯 2014本科C++ B组 地宫取宝 DFS+记忆化搜索

历届试题 地宫取宝  

时间限制：1.0s   内存限制：256.0MB

问题描述

　　X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。

　　地宫的入口在左上角，出口在右下角。

　　小明被带到地宫的入口，国王要求他只能向右或向下行走。

　　走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

　　当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。

　　请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

输入格式

　　输入一行3个整数，用空格分开：n m k
(1<=n,m<=50, 1<=k<=12)

　　接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值

输出格式

　　要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 1000000007 取模的结果。

样例输入

2 2 2
1 2
2 1

样例输出

2

样例输入

2 3 2
1 2 3
2 1 5

样例输出

14

话说这个题目意图还是蛮明显的，深搜完后返回所有满足的解的个数，不过这个善意的题目，要想完全正确还是学需要在处理时注意很多方面。

首先，先来谈第一个问题，写出其状态转移方程，我们要求的解是从原点手握价值最大的宝物v开始经过不同的路径到终点获得K件宝物的路径总数，我们姑且将此状态记为

d(1,1,k(初始为0，还没拿宝贝),-1(此时手上没有宝物，值记为-1))

那么从此状态出发，可以将其转移为如下的决策

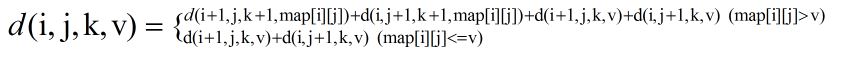
这里在补充说明用状态转移方程可以方便将原问题分解成若干个与原问题相同的子问题，且规模变小。

第二个问题，如果仅仅这样的话，必然存在重复计算的问题，为此必须要采取记忆化搜索的方式，对于已经计算过的结点保存其值，就这条题目而言，必须要用一个四维数组保存，因为它的状态跟位置，个数以及当前最大的宝物价值有关。当重复遍历这个结点时，直接传值。

第三个问题，细节决定成败！！

1.类型用long long稳妥，因为即使MOD了，但是如果两个数加起来还有可能超int。

2.我自己做的时候没注意的一个小错误，导致最后始终不对的疏忽。我错误的把r[MAXN][MAXN][15][15]的初始化为了0，这绝对不正确，因为有可能以某种方式走的状态就是无解，就是0，必须将初始值赋为-1。

3.对于有宝物的初始价值为-1，比较好的处理方式是，最后存放是第四维的下标后移一位

4.这里还要注意,k最多是13，不会超过这个值，所以第三维只要14就够了

其它的就看代码吧：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define MAXN 60
 #define MOD %1000000007
 using namespace std;
 long long r[MAXN][MAXN][][];//保存状态
 long long map[MAXN][MAXN];//初始地图
 long long m,n,num;
 long long dfs(long long i,long long j,long long k,long long v)
 {
     long long s=,t;
     if(r[i][j][k][v+]!=-)
         return r[i][j][k][v+];
     if(i==m&&j==n)//到达终点
     {
         if(k==num)
         {
             r[m][n][k][v+]=;
             return r[m][n][k][v+];
         }
         else if(k==num-&&map[m][n]>v)
         {
             r[m][n][k][v+]=;
             return r[m][n][k][v+];
         }
         else
         {
             r[m][n][k][v+]=;
             return r[m][n][k][v+];
         }
     }
     else
     {
         if(map[i][j]>v)
         {
             t=map[i][j];
             if(i+<=m)
             s=(s+dfs(i+,j,k+,t)MOD+dfs(i+,j,k,v)MOD)MOD;
             if(j+<=n)
             s=(s+dfs(i,j+,k+,t)MOD+dfs(i,j+,k,v)MOD)MOD;
         }
         else
         {
             if(i+<=m)
             s=(s+dfs(i+,j,k,v)MOD)MOD;
             if(j+<=n)
             s=(s+dfs(i,j+,k,v)MOD)MOD;
         }
         r[i][j][k][v+]=s MOD;
         return r[i][j][k][v+];
     }
 }
 int main()
 {
 //    freopen("data.in","r",stdin);
 //    freopen("data.out","w",stdout);
     memset(r,-,sizeof(r));
     long long i,j,p,q;
     cin>>m>>n>>num;
     for(i=;i<=m;i++)
         for(j=;j<=n;j++)
             cin>>map[i][j];
     dfs(,,,-);
     cout<<r[][][][]<<endl;
     return ;
 }