[poj2778]DNA Sequence(AC自动机+矩阵快速幂)

题意：有m种DNA序列是有疾病的，问有多少种长度为n的DNA序列不包含任何一种有疾病的DNA序列。（仅含A,T,C,G四个字符）

解题关键：AC自动机，实际上就是一个状态转移图，注意能少取模就少取模，尤其是在快速幂的时候，消耗时间极其巨大，此题效率差10倍。

先+=在进行取模，两者分开，也可以快1倍。

按照AC自动机建立邻接矩阵，其中不含病毒模式串的位置可以到达，

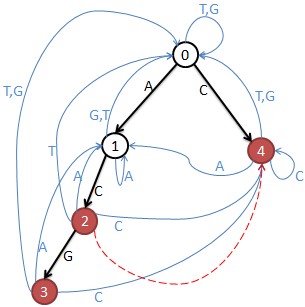
其中上图矩阵为：

2 1 0 0 1

2 1 1 0 0

1 1 0 1 1

2 1 0 0 1

2 1 0 0 1

去掉病毒结点之后，变为

2 1

2 1

转移方程：$dp[u] = \sum\limits_{v -  > u} {dp[v]} $

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<queue>
 using namespace std;
 typedef long long ll;
 const int N=;
 const int MAXN=;
 struct mat{
     ll m[][];
 };
 ll m,n;
 ll mod=;
 struct Trie{
     int Next[MAXN][N],Fail[MAXN],root,tot;
     bool End[MAXN];
     int newnode(){
         for(int i=;i<N;i++) Next[tot][i]=-;
         End[tot++]=false;
         return tot-;
     }
     void init(){
         tot=;
         root=newnode();
     }
     void insert(char buf[]){
         int len=strlen(buf),now=root,k;
         for(int i=;i<len;i++){
             if(buf[i]=='A') k=;
             else if(buf[i]=='G') k=;
             else if(buf[i]=='C') k=;
             else k=;
             if(Next[now][k]==-)  Next[now][k]=newnode();
             now=Next[now][k];
         }
         End[now]=true;
     }
     void build(){
         queue<int>que;
         Fail[root]=root;
         for(int i=;i<N;i++){
             if(Next[root][i]==-) Next[root][i]=root;
             else{
                 Fail[Next[root][i]]=root;
                 que.push(Next[root][i]);
             }
         }
         while(!que.empty()){
             int now=que.front();
             que.pop();
             if(End[Fail[now]]) End[now]=true;
             for(int i=;i<N;i++){
                 if(Next[now][i]==-) Next[now][i]=Next[Fail[now]][i];
                 else{
                     Fail[Next[now][i]]=Next[Fail[now]][i];
                     que.push(Next[now][i]);
                 }
             }
         }
     }
     mat get_mat(int len){
         mat B={};
         for(int i=;i<len;i++){
             for(int j=;j<N;j++){
                 if(End[Next[i][j]]==false) B.m[i][Next[i][j]]++;//不能直接置1
             }
         }
         return B;
     }
 };

 mat mul(mat &A,mat &B,int len){
     mat C={};
     for(int i=;i<len;i++){
         for(int j=;j<len;j++){
             for(int k=;k<len;k++){
                 C.m[i][j]+=A.m[i][k]*B.m[k][j];
             }
             C.m[i][j]%=mod;
         }
     }
     return C;
 }

 mat pow(mat A,ll n,int len){
     mat B={};
     for(int i=;i<len;i++) B.m[i][i]=;
     while(n){
         if(n&) B=mul(B,A,len);
         A=mul(A,A,len);
         n>>=;
     }
     return B;
 }

 Trie ac;
 char buf[];
 int main(){
     while(scanf("%lld%lld",&m,&n)!=EOF){
         ac.init();
         for(int i=;i<m;i++){
             scanf("%s",buf);
             ac.insert(buf);
         }
         ac.build();
         mat B=ac.get_mat(ac.tot);
         B=pow(B,n,ac.tot);
         ll res=;
         for(int i=;i<ac.tot;i++){
             res+=B.m[][i];
         }
         printf("%lld\n",res%mod);
     }
     return ;
 }