loj558 「Antileaf's Round」我们的CPU遭到攻击

考完了可以发题解了。

做法是link-cut tree维护子树信息，并不需要维护黑树白树那些的。

下面是一条重链：

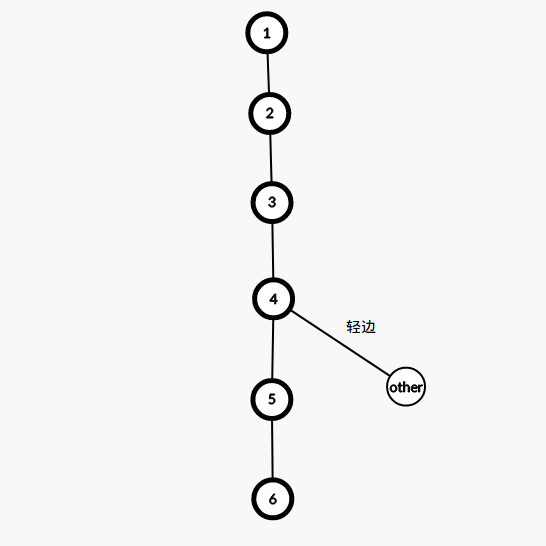
如果4是根的话，那么在splay上是这样的：

在splay中，子树的信息都已经计算完毕，那么需要计算这个子树的答案。

这个子树有4个部分：

4：树根。

1,2,3：树根上面的点。

5,6：树根下面的点。

other：树根的虚子树。

那么简化一下：

显然是需要记录答案的，还要记录什么？

• 3,4会受到1,2的影响，所以答案要加上3,4中黑点数×1,2中权值和
• 1会受到2的影响，所以答案要加上1中黑点数×2中权值和
• 没了。剩下的都在原来就计算好了。

所以还要记子树黑点数和权值和。

然后就做完了。

注意一下，splay有reverse操作，所以还要记一个反的答案（丧心病狂，，，），不过虚子树答案不用反过来。

// It is made by XZZ
#include<cstdio>
#include<algorithm>
#define il inline
#define rg register
#define vd void
#define sta static
typedef long long ll;
il int gi(){
	rg int x=0,f=1;rg char ch=getchar();
	while(ch<'0'||ch>'9')f=ch=='-'?-1:f,ch=getchar();
	while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
const int maxn=4e5+1;
int ch[maxn][2],fa[maxn],w[maxn];
ll lans[maxn],rans[maxn],_ans[maxn],tot[maxn],_tot[maxn],W[maxn];
bool col[maxn];
bool rev[maxn];
typedef const int& ci;
il vd Rev(ci x){if(x)rev[x]^=1,std::swap(ch[x][0],ch[x][1]),std::swap(lans[x],rans[x]);}
il bool isrt(ci x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
il vd down(ci x){
	if(!x)return;
	if(!isrt(x))down(fa[x]);
	if(rev[x])Rev(ch[x][0]),Rev(ch[x][1]),rev[x]=0;
}
il vd upd(ci x){
	if(!x)return;
	W[x]=W[ch[x][0]]+W[ch[x][1]]+w[x];
	tot[x]=_tot[x]+tot[ch[x][0]]+tot[ch[x][1]]+col[x];
	lans[x]=_ans[x]+lans[ch[x][0]]+lans[ch[x][1]]+(_tot[x]+tot[ch[x][1]]+col[x])*(w[x]+W[ch[x][0]]);
	rans[x]=_ans[x]+rans[ch[x][1]]+rans[ch[x][0]]+(_tot[x]+tot[ch[x][0]]+col[x])*(w[x]+W[ch[x][1]]);
}
il vd rotate(ci x){
	rg int y=fa[x],z=fa[fa[x]],o=x==ch[y][1];
	if(!isrt(y))ch[z][y==ch[z][1]]=x;fa[x]=z;
	ch[y][o]=ch[x][!o];fa[ch[x][!o]]=y;
	fa[y]=x;ch[x][!o]=y;
	upd(y);
}
il vd splay(ci x){
	down(x);
	rg int y,z;
	for(y=fa[x],z=fa[y];!isrt(x);rotate(x),y=fa[x],z=fa[y])
		if(!isrt(y))rotate(((x==ch[y][1])==(y==ch[z][1]))?y:x);
	upd(x);
}
il vd access(int x){
	for(rg int y=0;x;x=fa[y=x]){
		splay(x);
		_tot[x]+=tot[ch[x][1]]-tot[y];
		_ans[x]+=lans[ch[x][1]]-lans[y];
		ch[x][1]=y;
		upd(x);
	}
}
il vd makert(ci x){access(x),splay(x);Rev(x);}
il vd link(ci x,ci y){
	makert(x),makert(y);
	_tot[x]+=tot[y];
	_ans[x]+=lans[y];
	fa[y]=x;upd(x);
}
il vd cut(ci x,ci y){
	makert(x),access(y),splay(y);
	int z=ch[y][0];
	ch[z][0]=fa[y]=ch[x][0]=fa[z]=0;
	upd(y);
}
int main(){
	int n=gi(),m=gi(),k=gi(),cnt=n,u,v,_w;
	while(m--){
		u=gi(),v=gi(),_w=gi();
		++cnt;w[cnt]=W[cnt]=_w;link(u,cnt),link(v,cnt);
	}
	char opt[2];
	while(k--){
		scanf("%s",opt);
		if(opt[0]=='L'){
			u=gi(),v=gi(),_w=gi();
			w[++cnt]=_w;link(u,cnt),link(v,cnt);
		}else if(opt[0]=='C'){
			u=gi(),v=gi();
			makert(u),access(v),splay(v);
			int z=ch[v][0];
			if(ch[z][1])z=ch[z][1];
			cut(u,z),cut(v,z);
		}
		else if(opt[0]=='F')u=gi(),makert(u),col[u]^=1,upd(u);
		else if(opt[0]=='Q')u=gi(),makert(u),printf("%lld\n",lans[u]);
	}
	return 0;
}

2.4KB