[Codeforces526F]Pudding Monsters 分治

F. Pudding Monsters

time limit per test

2 seconds

memory limit per test

256 megabytes

In this problem you will meet the simplified model of game Pudding Monsters.

An important process in developing any game is creating levels. A game field in Pudding Monsters is an n × n rectangular grid, n of its cells contain monsters and some other cells contain game objects. The gameplay is about moving the monsters around the field. When two monsters are touching each other, they glue together into a single big one (as they are from pudding, remember?).

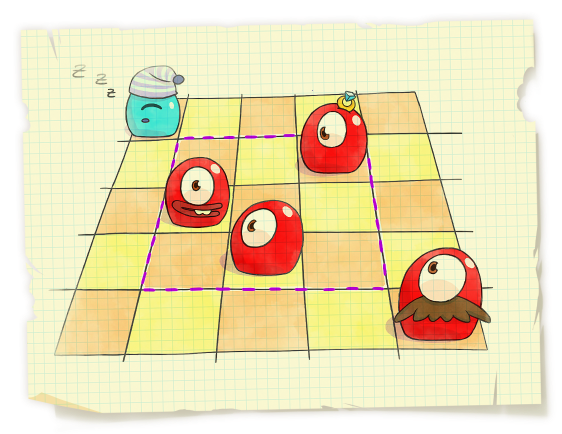
Statistics showed that the most interesting maps appear if initially each row and each column contains exactly one monster and the rest of map specifics is set up by the correct positioning of the other game objects.

A technique that's widely used to make the development process more efficient is reusing the available resources. For example, if there is a large n × n map, you can choose in it a smaller k × k square part, containing exactly k monsters and suggest it as a simplified version of the original map.

You wonder how many ways there are to choose in the initial map a k × k (1 ≤ k ≤ n) square fragment, containing exactly k pudding monsters. Calculate this number.

Input

The first line contains a single integer n (1 ≤ n ≤ 3 × 105) — the size of the initial field.

Next n lines contain the coordinates of the cells initially containing monsters. The i-th of the next lines contains two numbers ri, ci(1 ≤ ri, ci ≤ n) — the row number and the column number of the cell that initially contains the i-th monster.

It is guaranteed that all ri are distinct numbers and all ci are distinct numbers.

Output

Print the number of distinct square fragments of the original field that can form a new map.

Examples

input

5
1 1
4 3
3 2
2 4
5

output

10

题解：

考试的时候这道题真是吓到我了。。一开始以为是一道单纯的数数题，后来发现并不简单。。。

我们把这个棋盘模型抽象一下，这个棋盘由于

Statistics showed that the most interesting maps appear if initially each row and each column contains exactly one monster and the rest of map specifics is set up by the correct positioning of the other game objects.

也就是说，一行一列只有1个怪物，所以我们可以把它抽象为（化简为）一个1～n的排列

如果定义max（l，r）为区间[l,r]的最大值，min（l，r）为区间[l,r]的最小值，

我们需要的目标正方形，就对应这个排列中的某一个区间[l,r]，并且满足max（l，r）-min（l，r）==r-l

接下来是关键的一步：我们考虑分治统计这些合法区间（似乎有一些类似cdq？）。

也就是说，如果设f（l，r）为区间[l,r]的合法区间数量，mi=（l+r)>>1

那么f（l，r）=f（l，mi）+f（mi+1，r）+『跨中点的合法解数量』

接下来我们考虑如何统计跨中点的合法解数量。

对于跨中点的合法解，其可能情况有4种：

1°max（l，r），min（l，r）均在左侧

2°max（l，r），min（l，r）均在右侧

3°max（l，r）在左侧，min（l，r）在右侧

4°max（l，r）在右侧，min（l，r）在左侧

简单来说，就是极值“在同侧”和“在异侧”两种情况

如果极值在同侧，我们可以枚举一个端点，并且计算出区间长度，从而得到另外一个端点，

最后判断是否合法，也即判断另外一侧是否有更大/小的极值

如果极值在异侧，我们依旧枚举其中一个端点，

（我们这里仅讨论最小值在左侧的情况，最小值在右侧的情况是与此对称的）

然后我们考虑上面的式子max（mi+1，r）-min（l，mi）==r-l

移项可得max（mi+1，r）-r==min（l，mi）-l

这样我们就可以枚举左端点，再用桶维护每个min（l，mi）-l对应的合法解个数（通过扫描右区间可得）

但要注意，min（l，mi）-l可能是负值，因此我们要给他加上一个较大值（比如N）

最后统计答案即可。代码见下：

 #include <cstdio>
 #include <cstring>
 using namespace std;
 typedef long long LL;
 const int N=;
 int n,A[N],cnt[N*+],maxl[N],minl[N],maxr[N],minr[N];
 inline int max(int a,int b){return a>b?a:b;}
 inline int min(int a,int b){return a<b?a:b;}
 LL divide(int l,int r)
 {
     if(l==r)return ;
     register int mi=(l+r)>>,i,j,k;
     LL ret=divide(l,mi)+divide(mi+,r);
     maxl[mi]=minl[mi]=A[mi],maxr[mi+]=minr[mi+]=A[mi+];
     for(i=mi-;i>=l;--i)maxl[i]=max(maxl[i+],A[i]),minl[i]=min(minl[i+],A[i]);
     for(i=mi+;i<=r;++i)maxr[i]=max(maxr[i-],A[i]),minr[i]=min(minr[i-],A[i]);
     for(i=l;i<=mi;++i)
     {
         j=i+maxl[i]-minl[i];
         if(j<=r&&j>mi&&maxr[j]<maxl[i]&&minr[j]>minl[i])ret++;
     }
     for(i=r;i>mi;--i)
     {
         j=i-(maxr[i]-minr[i]);
         if(j>=l&&j<=mi&&maxl[j]<maxr[i]&&minl[j]>minr[i])ret++;
     }
     for(i=mi,j=mi+,k=mi;i>=l;--i)
     {
         while(j<=r&&maxr[j]<maxl[i])--cnt[maxr[j]-j+N],++j;
         while(k<r&&minr[k+]>minl[i])++k,++cnt[maxr[k]-k+N];
         ret+=max(cnt[minl[i]-i+N],);
     }
     for(i=mi+;i<=r;++i)cnt[maxr[i]-i+N]=;
     for(i=mi,j=mi+,k=mi;i>=l;--i)
     {
         while(j<=r&&minr[j]>minl[i])--cnt[minr[j]+j],++j;
         while(k<r&&maxr[k+]<maxl[i])++k,++cnt[minr[k]+k];
         ret+=max(cnt[maxl[i]+i],);
     }
     for(i=mi+;i<=r;++i)cnt[minr[i]+i]=;
     return ret;
 }
 int main()
 {
     scanf("%d",&n);int a,b;register int i,j;
     for(i=;i<=n;++i)scanf("%d%d",&a,&b),A[a]=b;
     printf("%I64d\n",divide(,n));
 }

这道题的代码实现不是很难，但是这种模型的转换，以及分治的想法是很excellent的，真是长见识了。

我不经常用分治的方法解题……以后刷题的时候要多想想这方面的解法了。