论文解读（DAEGC）《Improved Deep Embedded Clustering with Local Structure Preservation》

Paper Information

Title：《Attributed Graph Clustering: A Deep Attentional Embedding Approach》
Authors：Chun Wang、Shirui Pan、Ruiqi Hu、Guodong Long、Jing Jiang、C. Zhang
Source：2019, IJCAI
Other：96 Citations, 42 References
Paper：Download
Code：Download
Task：Graph Clustering、Graph Embedding、Node Clustering

---

Abstract

　　该方法侧重于属性图的构建，并使用 attention network 描述邻居节点对 target node 的重要性。

---

1 Introduction

　　目前研究现状：基于图表示学习的方法都是两阶段的方法 。

　　总结目前研究：重构拓扑结构以及重建节点表示的方法。

　　研究缺陷：拓扑结构和节点表示融合机制并不完美。

　　本文模型：$\text{DAEGC}$ [ a goal-directed graph attentional autoencoder based attributed graph clustering framework ]

　　重建节点表示：采用 $\text{graph attentional autoencoder }$：

• • $\text{Encoder}$ 可以同时学习节点内容以及图结构 ；
  • $\text{Decoder}$ 重建图拓扑结构 ；

　　训练模型：自训练模型 [ 高置信度分布指导模型训练 ]

　　本文模型与传统的 $\text{two-step}$ 方法的比较如 Figure 1 所示：

　　　　

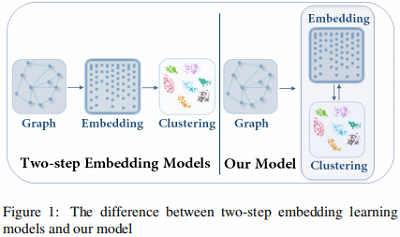
• 本文模型是将 $\text{node embedding}$ 和聚类放在一个统一的框架中学习。
• $\text{Two-step}$ 方法则是先学习 $\text{node embedding}$，然后进行聚类。

　　本文贡献：

• • 第一个提出图注意自编码器；
  • 提出了基于 $\text{goal-directed}$ 的图聚类框架；

---

2 Related Work

2.1 Graph Clustering

　　阐述早起方法的不顶用，以及感谢深度方法对图聚类的发展。

2.2 Deep Clustering Algorithms

　　铭记 DEC 深度聚类。

---

3 Problem Definition and Overall Framework

　　$\text{Graph basic definition}$ ：略。

　　给定图 $G$，图聚类的目的是将  $G$  中的节点划分为  $k$  个不相交  $\text{groups}$： ${G_1、G_2、···、G_k}$，使在同一  $\text{group}$ 的节点满足两个条件：

• • 彼此图结构相似 ；[ 社区结构类似 ]
  • 节点属性相似 ；

　　本文模型框架包括两个部分，如 Fig 2 所示 ：

• • Graph Attentional Autoencoder ：AE 以属性值和图结构作为输入，并通过最小化重构损失来学习潜在的 representation ；
  • Self-training Clustering ：根据学习到的 representation 进行聚类，并根据聚类结果对潜在 representation 进行操作；

　　

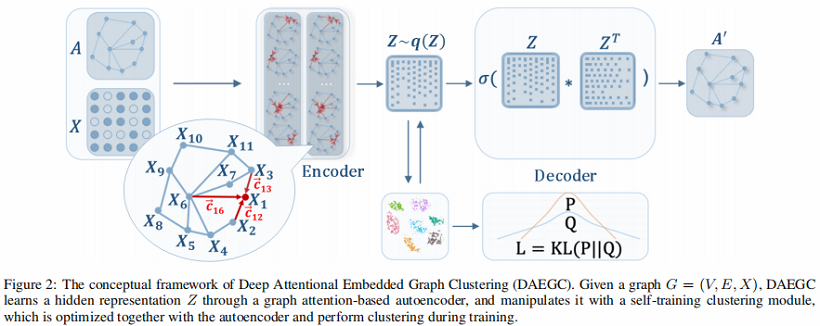
　　该框架将学习 graph embedding 和执行聚类放在一个统一的框架中，因此可以使每个组件彼此受益。

---

4 Proposed Method

　　本节先阐述 graph attentional autoencoder  [ 有效的学习图结构和 content information ] 生成 latent representation，然后阐述 self-training module 指导聚类。

4.1 Graph Attentional Autoencoder

　　Graph Attentional Autoencoder：通过关注每个节点的邻居来学习每个节点的 latent representation ，从而将 attribute values 与图结构信息 融入 latent representation。

　　首先：衡量 $\text{node}$ $i$ 的邻居 $N_i$  对于 $\text{node}$ $i$ 的影响，这里考虑的是不同邻居对 $\text{node}$ $i $ 的影响不一样，主要体现在对邻居赋予不同的权重。

　　　　$z_{i}^{l+1}=\sigma\left(\sum\limits _{j \in N_{i}} \alpha_{i j} W z_{j}^{l}\right)\quad\quad\quad(1)$

　　其中：

• • $z_{i}^{l+1}$  denotes the output representation of node  $i$ ；
  • $N_{i}$  denotes the neighbors of  $i$ ；
  • $\alpha_{i j}$  is the attention coefficient that indicates the importance of neighbor node  $j$  to node  $i$ ；
  • $\sigma$  is a nonlinerity function ；

　　对于 attention 系数   $\alpha_{i j}$ [ 重要度 ] 主要参考两个方面：

• 1. 属性值（attribute values） ；
  2. 拓扑距离（ topological distance ）；

　　Aspact 1：属性值

　　attention 系数 $\alpha_{i j}$ 可以表示为 由 $x_i$ 和 $x_j$ 拼接形成的单层前馈神经网络：

　　　　$c_{i j}=\vec{a}^{T}\left[W x_{i} \| W x_{j}\right]\quad \quad \quad(2)$

　　其中：

• • $\vec{a} \in R^{2 m^{\prime}}$ 是权重向量；　　

　　Aspact 2：拓扑距离

　　在 AE 的 $\text{Encoder}$ 中考虑高阶邻居信息（这里指 $ \text{t-order} $ 邻居），得到  $\text{proximity matrix} $ ：

　　　　$M=\left(B+B^{2}+\cdots+B^{t}\right) / t\quad \quad\quad(3)$

　　其中：

• • $B$ 是转移矩阵（transition matrix），当  $e_{i j} \in E$  有边相连，那么  $B_{i j}=1 / d_{i}$  ，否则  $B_{i j}=0$ 。
  • $M_{i j}$  表示 $\text{node}$  $i$ 和 $\text{node}$  $j$ 的 $t$  阶内的拓扑相关性。这意味着 如果 $\text{node}$  $i$ 和 $\text{node}$  $j$ 存在邻居关系（$t$ 阶之内），那么  $M_{i j}>0 $。

　　通常对每个 $\text{group}$ 中的 $\text{node}$ 做标准化：采用 $\text{softmax function}$

　　　　${\large \alpha_{i j}=\operatorname{softmax}_{j}\left(c_{i j}\right)=\frac{\exp \left(c_{i j}\right)}{\sum_{r \in N_{i}} \exp \left(c_{i r}\right)}} \quad \quad \quad(4)$

　　将 $\text{Eq.2}$ 中 $c_{ij}$ 带入，并添加上 $\text{topological weights }$  $M$ 和激活函数  $\delta$ ，那么  $\text{attention}$ 系数可以表示为：

　　　　${\large \alpha_{i j}=\frac{\exp \left(\delta M_{i j}\left(\vec{a}^{T}\left[W x_{i} \| W x_{j}\right]\right)\right)}{\sum_{r \in N_{i}} \exp \left(\delta M_{i r}\left(\vec{a}^{T}\left[W x_{i} \| W x_{r}\right]\right)\right)}} \quad\quad\quad(5)$

　　其中

• • 激活函数 $\delta$ 采用 $LeakyReLU$ ；
  • $x_{i}=z_{i}^{0}$ 作为问题的输入 ；

　　这里我们堆叠 $2$ 个 $\text{graph attention layers}$ ：

　　　　$z_{i}^{(1)}=\sigma\left(\sum \limits _{j \in N_{i}} \alpha_{i j} W^{(0)} x_{j}\right)\quad \quad \quad (6)$

　　　　$z_{i}^{(2)}=\sigma\left(\sum\limits _{j \in N_{i}} \alpha_{i j} W^{(1)} z_{j}^{(1)}\right)\quad \quad\quad(7)$

　　到这就 Encoder 就编码了 结构信息和属性信息（node attributes），并且我们最终的 $z_{i}=z_{i}^{(2)}$ 。

Inner product decoder

　　本文采用了简单的  $\text{Inner product decoder}$ [ 输入已经包括了属性值和拓扑结构 ] 去预测节点之间的连接：

　　　　$\hat{A}_{i j}=\operatorname{sigmoid}\left(z_{i}{ }^{\top} z_{j}\right)\quad \quad \quad (8)$

　　其中：

• • $\hat{A}$ 是重建后的图结构矩阵；　　

Reconstruction loss

　　通过最小化度量 $A$ 和 $\hat{A}$ 重构错误：

　　　　$L_{r}=\sum\limits _{i=1}^{n} \operatorname{loss}\left(A_{i, j}, \hat{A}_{i j}\right)\quad\quad \quad (9)$

4.2 Self-optimizing Embedding

　　除了优化重构误差外，我们还将 hidden embedding 输入一个自优化聚类模块，该模块最小化以下目标：

　　　　$L_{c}=K L(P \| Q)=\sum\limits_{i} \sum\limits _{u} p_{i u} \log \frac{p_{i u}}{q_{i u}}\quad\quad\quad(10)$

其中：

• $q_{iu}$度量 node embedding $z_{i}$ 和 cluster center embedding $\mu_{u}$ 之间的相似性，本文通过 Student's t-distribution 度量。同时它可以看作是每个节点的一个软聚类分配分布。；
• $p_{iu}$ 代表着目标分布，由于在Q中，具有高概率的软分配（靠近集群中心的节点）被认为是可信的，所以考虑将 $Q$ 提高到二次方，以增加高可信度；

　　　　${\large q_{i u}=\frac{\left(1+\left\|z_{i}-\mu_{u}\right\|^{2}\right)^{-1}}{\sum\limits _{k}\left(1+\left\|z_{i}-\mu_{k}\right\|^{2}\right)^{-1}}} \quad\quad\quad（11）$

　　　　${\large p_{i u}=\frac{q_{i u}^{2} / \sum_{i} q_{i u}}{\sum_{k}\left(q_{i k}^{2} / \sum_{i} q_{i k}\right)}}\quad \quad\quad(12) $

　　聚类损失迫使当前分布  $Q$  接近目标分布 $P$，从而将这些  “confident assignments”  设置为软标签来监督  $Q$  的嵌入学习。

　　算法概述

• • 首先使用没有用 selfoptimize clustering part 的自编码器获得初始 embedding ；
  • 其次为计算  Eq.11 ，先使用 $k-means$ 获得初始聚类中心 $\mu$
  • 然后根据 $L_c$  使用 SGD 进行优化更新 $\mu$ 和 $z$ 。

　　需要注意的是 ：$P$ 每 $5$ 个 iteration 更新一次，$Q$ 每个 iteration 更新一次。

　　算法步骤：

　　　　

4.3 Joint Embedding and Clustering Optimization

　　我们联合优化了自动编码器的嵌入和聚类学习，并定义了我们的总目标函数为：

　　　　$L=L_{r}+\gamma L_{c}\quad \quad\quad (13)$

　　其中：

• • $L_{r}$ 代表着 reconstruction loss  ；
  • $L_{c} $ 代表着 clustering loss ；
  • $ \gamma \geq 0 $ 控制着 $L_{r}$ 和  $L_{c} $ 的平衡 ；

　　最终 $v_{i}$ 的 soft label 通过 $Q$ 获得：

　　　　$s_{i}=\arg \underset{u}{\text{max}} \; q_{i u}\quad \quad\quad(14)$

　　我们的算法有以下优点

• • Interplay Exploitation ：structure and content information ;
  • Clustering Specialized Embedding：self-training clustering component ;
  • Joint Learning：Jointly optimizes the two parts of the loss functions ;

---

5 Experiments

5.1 Results

　　

　　

　　

---

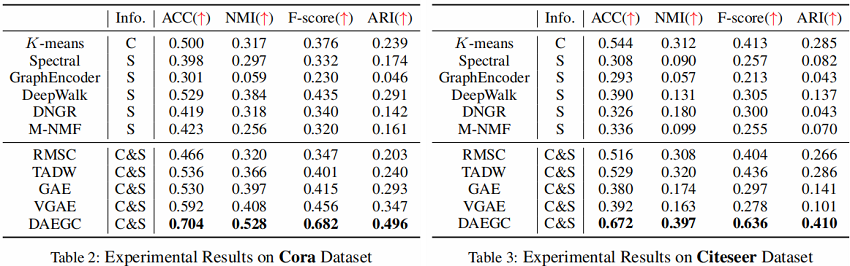
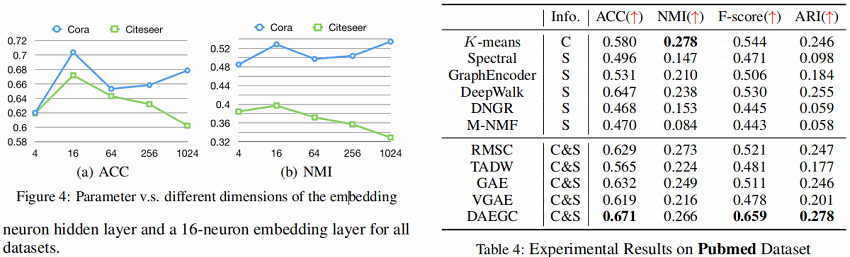
6 Conclusion

　　在本文中，我们提出了一种无监督的深度注意嵌入算法DAEGC，以在一个统一的框架中联合执行图聚类和学习图嵌入。学习到的图嵌入集成了结构信息和内容信息，专门用于聚类任务。虽然图的聚类任务自然是无监督的，但我们提出了一个自训练的聚类组件，它从“自信的”分配中生成软标签来监督嵌入的更新。对聚类损失和自编码器重构损失进行联合优化，同时得到图嵌入和图聚类结果。将实验结果与各种先进算法的比较，验证了DAEGC的图聚类性能。