CF1578I Interactive Rays：ICPC WF Moscow Invitational Contest I 题解

题意简述：在平面上有一个坐标 \((x_c,y_c)\) 和半径 \(r\) 都是整数的圆 \((1\leq r_c\leq \sqrt{x_c^2+y_c^2}-1)\)，你可以询问不超过 \(60\) 次一个从原点出发的射线 \((0,0)\to (x,y)\) 与圆的距离（若相交，则返回 \(0\)）。确定圆的坐标和半径。

\(|x_c|,|y_c|,r\le 10^5\)，你需要保证 \(|x|,|y|\leq 10^6\)。

一道有趣的计算几何，思维含量并不是很高（*3300 有点离谱），就是写起来麻烦了些。比赛的时候花了四个小时写这题，结果发现前面两个半小时写的东西完全没有用（狂笑）。

---

Step 1：旋转坐标轴规避分类讨论

首先我们得确定这个圆的大致位置，也就是在哪个象限。因为如果对于四个象限分别分类讨论很麻烦，不如旋转坐标轴使得这个圆落在某些固定的象限，每次旋转 \(90^{\circ}\)。不妨将圆心旋转到 \(x\) 轴上方，且确保这个圆不经过第三象限，这是可以同时做到的：

我们可以通过询问 \((0,\pm i)\) 与 \((\pm i,0)\) 来确定圆和坐标轴是否有交。

• 若没有交点，将坐标轴旋转使得圆落在第一象限。
• 若有一个交点，将坐标轴旋转使得圆落在第一、二象限。
• 若有两个交点，将坐标轴旋转使得圆落在第一、二、四象限。

不要忘了旋转后询问要转回来。比如我们将坐标轴顺时针旋转 \(90^{\circ}\) 后，询问时需要将坐标逆时针旋转 \(90^{\circ}\)。

---

Step 2：二分找到与圆相切的射线

由于圆心在 \(x\) 轴上方，询问交互库 \((0,x)\ (x<0)\) 的返回值 \(d_0\) 显然是 \(\sqrt{x_c^2+y_c^2}-r\)：因为过圆心且垂直于射线的直线与射线没有交点，故最短距离为原点与圆心距离减去半径。

注意到根据三个方程我们可以直接解出 \((x,y,r)\)，\(d_0=\sqrt{x_c^2+y_c^2}-r\) 已经是其中一个了。只需要再找到两个和圆距离 \(\neq d_0\) 且 \(\neq 0\) 的射线即可，称其为合法射线。

但是我们不能随便询问！因为可以构造一个与 \(y=kx\) 非常相近且半径非常大的圆，例如与 \(y=-x\) 几乎相切的 \((50000,50000,70709)\)，使得合法的射线范围非常小。因为一旦稍有偏移，我们询问到的是 \(d_0\)，要么就是 \(0\)（上述例子中，只有 \(y=-x\) 和过原点的圆的两条切线之间所夹住的区域合法）。而我们不知道出题人会构造什么毒瘤数据，这也意味着我们不能询问固定的射线，这样是没有前途的。

但注意到距离切线非常近（指与切线夹角非常小且与圆相离的射线范围）的那一块区域是合法的，这启发我们二分出几乎与圆相切（但与圆相离）的两条射线 \(a:(0,0)\to (x_a,y_a)\) 与 \(b:(0,0)\to (x_b,y_b)\)。具体怎么二分呢，想象一个 \((2\times10^6)\times (2\times 10^6)\) 的盒子包住了整个坐标轴。我们在从左逼近时，若返回值 \(>\rm eps\) 则认为与圆相离，向顺时针方向二分，否则认为与圆相交或相切，向逆时针方向二分。从右逼近则相反。

代码中寻找射线 \(a\) 只在第二象限内（原因在接下来会提到），因为圆心在 \(x\) 轴上方导致就算二分不到与切线很相近的位置，我们也可以找到不同于 \(d_0\) 和 \(0\) 的其它合法射线（想一想，为什么？Hint：\(10^6>10^5\)）。

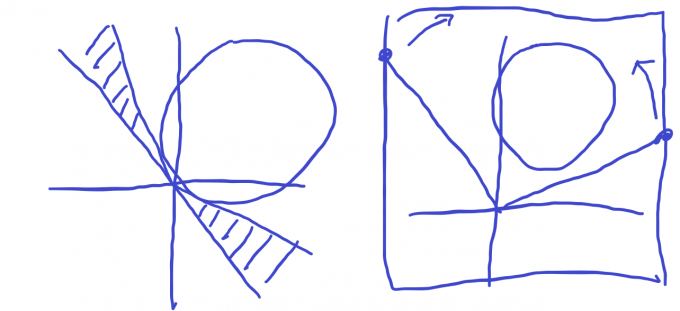
Step 3：枚举 \(r\) 并根据 \(d_0,d_a\) 求出 \((x,y)\)

根据圆与 \(a\) 的距离 \(d_a\) 以及 \(d_0\) 仍不足以确定这个圆：两个方程，三个变量。如果再加上 \(d_b\) 那么算起来太麻烦，精度爆炸怎么办？没有关系，注意到 \(r\) 是整数并且 \(\leq 10^5\)，我们直接枚举 \(r\) 并根据 \(d_0,d_a\) 算出 \(x,y\)，再检查当前的圆 \((x,y,r)\) 与 \(b\) 的距离是否等于 \(d_b\)。若相等则说明 \((x,y,r)\) 即为答案。这样精度就很优秀了。

怎么算 \(x,y\)：注意到射线 \(a\) 在第二象限内，设其与 \(x\) 轴负半轴的夹角为 \(\alpha\)，先将坐标轴逆时针旋转 \(\alpha\) 使得 \(a\) 落在 \(x\) 轴负半轴上，我们设原来的 \(x,y\) 经过这样的变换后新的坐标为 \(x_T,y_T\)。我们很容易求出 \(x_T,y_T\)：\(y_T\) 就是 \(r+d_a\)，而 \(d_0\) 在这样的变换下是不会变的（旋转变换不改变两点之间的距离），因此 \(x_T^2+y_T^2=(r+d_0)^2\)。解得 \(|x_T|\) 后还需要确定符号：究竟是在新坐标系的第一象限还是第二象限。这个可以通过求得 \(a\) 后询问交互库 \((-x_a,-y_a)\) 得到 \(d_a'\)，若 \(d_a<d_a'\) 说明 \(T\) 在第二象限，令 \(x_T\gets -|x_T|\)，否则 \(T\) 在第一象限，\(x_T\gets |x_T|\)。

注意到我们将坐标轴逆时针旋转了 \(\alpha\) 角度，因此还要顺时针转回来。将其乘以

\[\begin{bmatrix}\cos (-\alpha)&-\sin(-\alpha)\\\sin (-\alpha)&\cos(-\alpha)\end{bmatrix}
\]

即

\[\begin{bmatrix}\cos \alpha&\sin\alpha\\-\sin \alpha&\cos\alpha\end{bmatrix}
\]

即可。根据 \(\alpha\in\left[0,\dfrac \pi 2\right]\) 进行了化简。至于怎么算圆到射线的距离，点积搞搞就好了吧，实在不行可以像我一样上网现学。

至此，本题被我们完美解决。时间复杂度 \(\mathcal{O}(r)\)，询问次数为 \(2\log V\)，其中 \(V\) 是询问最大范围。代码中使用 \(V=2\times 10^5\)，一个测试点大约询问 \(50\) 次。

const ld eps=1e-5;
const ll N=2e5;

ld max(ld x,ld y){return x>y?x:y;}
bool Eq(ld x,ld y){return fabs(x-y)<eps;}
bool Isz(ld x){return fabs(x)<eps;}

ld up,down,left,right;
ld dis(ld x1,ld y1,ld x2,ld y2){
	return sqrt((x1-x2)*(x1-x2)+((y1-y2)*(y1-y2)));
}
ld dis(ld x1,ld y1,ld x2,ld y2,ld r){
	ld dot=x1*x2+y1*y2,d=dis(0,0,x2,y2);
	if(dot<eps)return max((ld)0,d-r);
	ld need=dot/dis(0,0,x1,y1);
	return max((ld)0,sqrt(d*d-need*need)-r);
}

int swp,type;
void ref(int &x,int &y){int t=y; y=x,x=-t;}
ld query(int x,int y){
	for(int j=1;j<=swp;j++)ref(x,y);
	std::cout<<"? "<<x<<" "<<y<<std::endl;
	ld res; std::cin>>res;
	return res;
}
void answ(int x,int y,int r){
	for(int j=1;j<=swp;j++)ref(x,y);
	std::cout<<"! "<<x<<" "<<y<<" "<<r<<std::endl,exit(0);
}
void answer(ld x,ld y,ld r){
	int xx=x<0?x-eps:x+eps;
	int yy=y<0?y-eps:y+eps;
	return answ(xx,yy,r+eps);
}

int main(){
	up=query(0,10),down=query(0,-10);
	left=query(-10,0),right=query(10,0);
	type=Isz(up)+Isz(down)+Isz(left)+Isz(right);
	if(type==0){
		ld mx=max(max(up,down),max(left,right));
		if(down==mx&&right==mx)swp=1;
		if(right==mx&&up==mx)swp=2;
		if(up==mx&&left==mx)swp=3;
	}
	if(type==1){
		if(Isz(left))swp=1;
		if(Isz(down))swp=2;
		if(Isz(right))swp=3;
	}
	if(type==2){
		if(Isz(left)&&Isz(up))swp=1;
		if(Isz(down)&&Isz(left))swp=2;
		if(Isz(right)&&Isz(down))swp=3;
	}
	up=query(0,10),down=query(0,-10);
	left=query(-10,0),right=query(10,0);
	ll l=1,r=N*2-1,xx,yy; ld res;
	while(l<r){
		ll m=l+r>>1;
		xx=-std::min(N,m),yy=N-max(0ll,m-N);
		(res=query(xx,yy))>1e-6?r=m:l=m+1;
	}
	xx=-std::min(N,l),yy=N-max(0ll,l-N);
	ld upl=query(xx,yy),downr=query(-xx,-yy);
	ld mdis=std::min(upl,downr);

	ll xx2,yy2; l=1,r=N*3-1;
	while(l<r){
		ll m=(l+r>>1)+1;
		xx2=std::min(N,m),yy2=-N+max(0ll,m-N);
		(res=query(xx2,yy2)>1e-6)?l=m:r=m-1;
	}
	xx2=std::min(N,l),yy2=-N+max(0ll,l-N);
	res=query(xx2,yy2);
	for(int r=1;r<=1e5;r++){
		ld y=mdis+r,x=sqrt((down+r)*(down+r)-y*y);
		ld sn=(ld)fabs(yy)/(ld)(sqrt(xx*xx+yy*yy));
		ld cs=(ld)fabs(xx)/(ld)(sqrt(xx*xx+yy*yy));
		if(Eq(mdis,upl))x=-x;
		ld x0=x*cs+y*sn,y0=-x*sn+y*cs; x=x0,y=y0;
		if(Eq(res,dis(xx2,yy2,x,y,r)))answer(x,y,r);
	}
	return 0;
}
// qwq Kelly qwq