Noip模拟29（瞎眼忌） 2021.8.3

T1 最长不下降子序列

在此记录自己的瞎眼。。。

考场上像一个傻$der$，自己为了防范上升序列和不下降序列的不同
特意的造了一组$hack$数据来卡自己：（第一行是序列长度，第二行是序列）

6
1 5 2 3 3 7

结果。。。眼瞎把$LIS$ 看成了$4$，$TMD$是5鸭！！。。。。

严重怀疑$IQ$。。。。。

好了好了，就是又翻车了。。。连个暴力也没打对。。。。

正解可以考场上打表想到，不过场上大力攻克$T3$线段树发现循环节也没细想，抡了个暴力去码T3了

发现$D$只有$150$，那么最劣情况循环节为$150$。

由于循环可能不从第一个开始，也可能不是在最后一个刚好结束，

可以找到$pre$和$nxt$，再接上中间的$150$个循环节。

为什么是$150$个？ 因为我不想考虑有几个循环节的贡献不为$1$了。。

不过经过考虑应该接入 循环节长度-1 个循环节

考虑循环节对$LIS$的贡献

对于前$len$组循环节，他的贡献可能是$1 or 2$

例如，循环节为$1,2,3,4$

循环了四次:

$1,2,3,4,1,2,3,4,1,2,3,4$ ，$LIS$显然为$1,2,2,3,3,4$，

如果在他的后面再接一组循环节，这个循环节的贡献只能是$1$

即， $1,2,2,3,3,4,4$。所以只考虑将$len-1$组循环节接入要求的序列

到此，我们就可以暴力的生成长度为$pre+nxt+len*(len-1)$的序列求出$LIS$

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=10000005,inf=0x3fffffff;
 5 int n,A,B,C,D,t,tr[NN],a[NN],dis[NN],has,ans;
 6 int vis[NN];
 7 inline int lowbit(int x){return x&(-x);}
 8 inline void update(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) tr[i]=max(tr[i],v);}
 9 inline int query(int x){int ans=0; for(int i=x;i;i-=lowbit(i)) ans=max(ans,tr[i]); return ans;}
10 inline void work(){
11     dis[1]=a[1]=t;for(int i=2;i<=n;i++)
12         dis[i]=a[i]=(A*a[i-1]%D*a[i-1]%D+B*a[i-1]%D+C)%D;
13     sort(dis+1,dis+n+1); has=unique(dis+1,dis+n+1)-dis-1;
14     for(int i=1;i<=n;i++) a[i]=lower_bound(dis+1,dis+has+1,a[i])-dis;
15     for(int i=1;i<=n;i++) update(a[i],query(a[i])+1);
16     printf("%lld\n",query(has));
17 }
18 namespace WSN{
19     inline short main(){
20         scanf("%lld%lld%lld%lld%lld%lld",&n,&t,&A,&B,&C,&D);
21         if(n<=1000000) {work();return 0;}
22         int pos=1,pre,nxt,len;a[1]=t;
23         while(1){
24             ++pos; a[pos]=(a[pos-1]*a[pos-1]%D*A%D+a[pos-1]*B%D+C)%D;
25             if(!vis[a[pos]]) vis[a[pos]]=pos;
26             else{
27                 len=pos-vis[a[pos]];
28                 pre=vis[a[pos]]-1;
29                 nxt=(n-pre)%len;
30                 ans=(n-pre-nxt-len*150)/len;
31                 n=pre+len*150+nxt;
32                 break;
33             }
34         }
35         dis[1]=a[1]=t;
36         for(int i=2;i<=n;i++)
37             dis[i]=a[i]=(a[i-1]*a[i-1]%D*A%D+a[i-1]*B%D+C)%D;
38         sort(dis+1,dis+n+1); has=unique(dis+1,dis+n+1)-dis-1;
39         for(int i=1;i<=n;i++) a[i]=lower_bound(dis+1,dis+has+1,a[i])-dis;
40         for(int i=1;i<=n;i++) update(a[i],query(a[i])+1);
41         printf("%lld\n",query(has)+ans);
42         return 0;
43     }
44 }
45 signed main(){return WSN::main();}

保证代码的正确性以及细节的较多性

我们使用了较高级的避免细节错误的算法——

组合拳

即在$1e6$以下的数据都直接暴力生成序列，超过$1e6$的序列都会有超过$150$组循环节，不必考虑少于$len-1$组循环节的情况

T2 完全背包问题

依旧组合拳

首先将$v$数组排序，如果$v_0>=L$

直接进入第二算法。

设$f_{k,i,j}$表示前$k$个物品中，大体积物品数量不超过$i$件，是否存在总体积为$j$的方案列出状态转移方程：

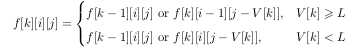
然后对于m$O(1)$出解就可以了，注$bitset$优化

对于其他的情况，观察数据范围，根本无法开数组

考虑将W缩小

发现只求$W%v_0$就可以，因为W剩下的那些体积都可以用无限个$v_0$补足

我们设$f_{k,i,j}$表示前$k$个物品中，大体积不超过$i$件，所有方案的总体积最小值，并要求其$mod,v_0==j$

只需判断W与$f_{n,C,Wmodv_0}$的大小就行

注意到$dp$状态转移是呈环状，考虑使用单源最短路求解，关于图的建立，这里直接粘贴题解部分，说的很详细。

剩下的注意一下跑出来的最短路$dp$是正好选择了$i$个，我们需要让$dp$数组符合定义

应将其覆盖，符合定义

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 int n,m,v[55],L,C,MOD;
 5 inline void work(){
 6     bitset<300005> dp[55][35];
 7     dp[0][0][0]=1;
 8     for(int i=1;i<=n;i++)
 9         for(int j=0;j<=C;j++)
10             for(int k=0;k<=300005;k++)
11                 if(k>=v[i]) dp[i][j][k]=dp[i-1][j][k]|dp[i][j-1][k-v[i]];
12                 else dp[i][j][k]=dp[i-1][j][k];
13     while(m--){
14         int w; scanf("%lld",&w);
15         if(w>300005||!dp[n][C][w]) puts("No");
16         else puts("Yes");
17     }
18 }
19 int dis[10005],S=10004,f[55][35][10005];
20 bool vis[10005];
21 struct SNOW{int to,val,next;};SNOW e[800005]; int head[800005],rp;
22 struct node{
23     int q,data;
24     friend bool operator<(node a,node b){return a.data>b.data;}
25 };
26 inline void add(int x,int y,int z){e[++rp]=(SNOW){y,z,head[x]}; head[x]=rp;}
27 inline void dji(){
28     memset(dis,0x3f,sizeof(dis));
29     memset(vis,0,sizeof(vis));
30     priority_queue<node> Q;
31     int x,y; dis[S]=0;
32     Q.push((node){S,0});
33     while(!Q.empty()){
34         x=Q.top().q; y=Q.top().data; Q.pop();
35         if(!vis[x]){
36             vis[x]=true;
37             for(int i=head[x];i;i=e[i].next) if(dis[e[i].to]>y+e[i].val){
38                 dis[e[i].to]=y+e[i].val;
39                 Q.push((node){e[i].to,dis[e[i].to]});
40             }
41         }
42     }
43 }
44 namespace WSN{
45     inline short main(){
46         scanf("%lld%lld",&n,&m);
47         for(int i=1;i<=n;i++) scanf("%lld",&v[i]);
48         scanf("%lld%lld",&L,&C);
49         sort(v+1,v+n+1); MOD=v[1];
50         if(v[1]>=L){work(); return 0;}
51         memset(f[0],0x3f,sizeof(f[0]));
52         f[0][0][0]=0;
53         for(int k=1;k<=n;k++) for(int i=0;i<=C;i++){
54             if(v[k]<L){
55                 rp=0; memset(head,0,sizeof(head));
56                 for(int j=0;j<MOD;j++){
57                     add(S,j,f[k-1][i][j]);
58                     add(j,(j+v[k])%MOD,v[k]);
59                 }
60                 dji();
61                 for(int j=0;j<MOD;j++) f[k][i][j]=dis[j];
62             }
63             else{
64                 for(int j=0;j<MOD;j++)
65                     if(i)f[k][i][j]=min(f[k-1][i][j],f[k][i-1][(j-v[k]%MOD+MOD)%MOD]+v[k]);
66                     else f[k][i][j]=f[k-1][i][j];
67             }
68         }
69         for(int i=1;i<=C;i++){
70             for(int j=0;j<MOD;j++){
71                 f[n][i][j]=min(f[n][i][j],f[n][i-1][j]);
72             }
73         }
74         while(m--){
75             int w; scanf("%lld",&w);
76             w>=f[n][C][w%MOD]? puts("Yes"):puts("No");
77         }
78         return 0;
79     }
80 }
81 signed main(){return WSN::main();}

T3 最近公共祖先

题目较为简单，类似牛半仙，直接放代码了

 1 #include<bits/stdc++.h>
 2 #define lid (id<<1)
 3 #define rid (id<<1|1)
 4 using namespace std;
 5 const int NN=2e5+5,inf=1e9;
 6 int n,m,w[NN];
 7 char s[10];
 8 struct SNOW{int to,next;};SNOW e[NN<<1]; int head[NN],rp;
 9 int dfn[NN],rk[NN],son[NN],top[NN],siz[NN],dep[NN],fa[NN],cnt;
10 bool vis[NN];
11 inline void add(int x,int y){
12     e[++rp]=(SNOW){y,head[x]}; head[x]=rp;
13     e[++rp]=(SNOW){x,head[y]}; head[y]=rp;
14 }
15 inline void dfs1(int f,int x){
16     fa[x]=f; dep[x]=dep[f]+1; siz[x]=1;
17     for(int i=head[x];i;i=e[i].next){
18         int y=e[i].to;
19         if(y==f) continue;
20         dfs1(x,y); siz[x]+=siz[y];
21         if(siz[son[x]]<siz[y]) son[x]=y;
22     }
23 }
24 inline void dfs2(int x,int t){
25     dfn[x]=++cnt; rk[cnt]=x; top[x]=t;
26     if(son[x]) dfs2(son[x],t);
27     for(int i=head[x];i;i=e[i].next){
28         int y=e[i].to;
29         if(y!=son[x]&&y!=fa[x]) dfs2(y,y);
30     }
31 }
32 struct SNOWtree{
33     int ll[NN<<2],rr[NN<<2];
34     int maxn[NN<<2],laz[NN<<2];
35     inline void pushup(int id){
36         if(ll[id]==rr[id]) return;
37         maxn[id]=max(maxn[lid],maxn[rid]);
38     }
39     inline void pushdown(int id){
40         if(!laz[id]||ll[id]==rr[id]) return;
41         laz[lid]=max(laz[lid],laz[id]);
42         laz[rid]=max(laz[rid],laz[id]);
43         maxn[lid]=max(maxn[lid],laz[id]);
44         maxn[rid]=max(maxn[rid],laz[id]);
45         laz[id]=0;
46     }
47     void build(int id,int l,int r){
48         ll[id]=l; rr[id]=r;
49         if(l==r) return;
50         int mid=l+r>>1;
51         build(lid,l,mid); build(rid,mid+1,r);
52     }
53     void update(int id,int l,int r,int v){
54         if(l<=ll[id]&&rr[id]<=r){
55             maxn[id]=max(maxn[id],v);
56             laz[id]=max(laz[id],v);
57             return;
58         }pushdown(id);
59         int mid=ll[id]+rr[id]>>1;
60         if(l<=mid) update(lid,l,r,v);
61         if(r>mid) update(rid,l,r,v);
62         pushup(id);
63     }
64     int find(int id,int pos){
65         if(ll[id]==rr[id]) return maxn[id];
66         pushdown(id); int mid=ll[id]+rr[id]>>1;
67         if(pos<=mid) return find(lid,pos);
68         else return find(rid,pos);
69     }
70 }tr;
71 namespace WSN{
72     inline short main(){
73         scanf("%d%d",&n,&m);
74         for(int i=1;i<=n;i++) scanf("%d",&w[i]);
75         for(int i=1,x,y;i<n;i++) scanf("%d%d",&x,&y),add(x,y);
76         dfs1(0,1); dfs2(1,1); tr.build(1,1,n);
77         while(m--){
78             int v; scanf("%s%d",s,&v);
79             if(s[0]=='Q'){
80                 if(!tr.find(1,dfn[v])) puts("-1");
81                 else printf("%d\n",tr.find(1,dfn[v]));
82                 continue;
83             }
84             if(s[0]=='M'){
85                 tr.update(1,dfn[v],dfn[v]+siz[v]-1,w[v]);
86                 while(fa[v]&&!vis[v]){
87                     vis[v]=1;
88                     tr.update(1,dfn[fa[v]],dfn[v]-1,w[fa[v]]);
89                     tr.update(1,dfn[v]+siz[v],dfn[fa[v]]+siz[fa[v]]-1,w[fa[v]]);
90                     v=fa[v];
91                 }
92                 continue;
93             }
94         }
95         return 0;
96     }
97 }
98 signed main(){return WSN::main();}