LeetCode：BFS/DFS

BFS/DFS

在树专题和回溯算法中其实已经涉及到了BFS和DFS算法，这里单独提出再进一步学习一下

BFS

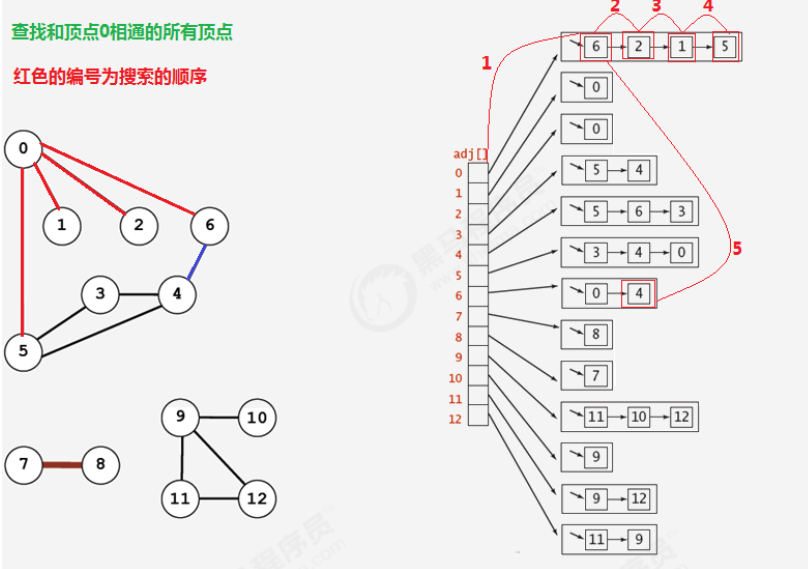
广度优先遍历 Breadth-First-Search

这部分的内容也主要是学习了labuladong公众号内的相关讲解

算法流程

1. 首先将开始节点放入队列中。
2. 从队列中取出第一个节点，并检验它是否为目标。
   • 如果找到目标，则结束搜索并回传结果。
   • 否则将它所有尚未检验过的直接子节点加入队列中。
3. 若队列为空，表示整张图都检查过了——亦即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。
4. 重复步骤 2。

算法模版

1. 一般模版：

   void bfs(Node start, Node target){
       // 使用双端队列，而不是数组
       Queue<TreeNode> queue = new ArrayDeque<>();
       // 注意：ArrayDeque不允许null值，LinkedList允许null值
       // Queue<TreeNode> queue = new LinkedList<>();
       // 记录层数
       int steps = 0;
       // 记录访问过的节点
       Set<Node> visited = new HashSet<>();
       queue.offer(start);
       while(!queue.isEmpty()){
           // 当前层的节点数
           int size = queue.size();
           // 遍历当前层的所有节点数
           for (int i=0; i<size; i++){
               Node node = queue.poll();
               result.add(node);
               // 判断节点是否满足，而决定是否返回等操作
               if(node.val == target.val){
                   return steps; // || return result;
               }
               // 将node周围的还未访问过的节点都加入队列中
               for(Node tmp: node.adj()){
                   if(!visited.contains(tmp)){
                       queue.offer(tmp);
                       visited.add(tmp);
               	}
               }
           }
           steps += 1; // 遍历完一层，层数+1
       }
       return;
   }
   

   相关题目：

   • 752. 打开转盘锁

   • 773. 滑动谜题

2. 针对树这种数据结构，因没有子节点回指向父节点的指针，因此可以不需要上述的 visited

   void bfs(TreeNode root){
          // 使用双端队列，而不是数组
          Queue<TreeNode> queue = new ArrayDeque<>();
          // 注意：ArrayDeque不允许null值，LinkedList允许null值
          // Queue<TreeNode> queue = new LinkedList<>();
          // 记录层数
          int steps = 0;
          queue.offer(root);
          while(!queue.isEmpty()){
              // 当前层的节点数
              int size = queue.size();
              // 遍历当前层的所有节点数
              for (int i=0; i<size; i++){
                  TreeNode node = queue.poll();
                  result.add(node);
                  // 判断节点是否满足，而决定是否返回等操作
                  if(node.left != null){
                      queue.offer(node.left);
                  }
                  if(node.right != null){
                      queue.offer(node.right);
                  }
              }
              steps += 1; // 遍历完一层，层数+1
          }
          return;
      }
   

   典型题目：

   • 513. 找树左下角的值，树专题已经做过了

   • 111. 二叉树的最小深度

带权最短距离

在堆专题中涉及到了带权的最短距离，即此时的节点到邻居之间的距离不是定值了，而是带有权重。

使用优先队列的 BFS 实现典型的就是 dijkstra 算法。dijkstra 算法主要解决的是图中任意两点的最短距离。

算法的基本思想是贪心，每次都遍历所有邻居，并从中找到距离最小的，本质上是一种广度优先遍历。

更具体的内容跳转：堆专题-总结-四大应用-带权最短距离

DFS

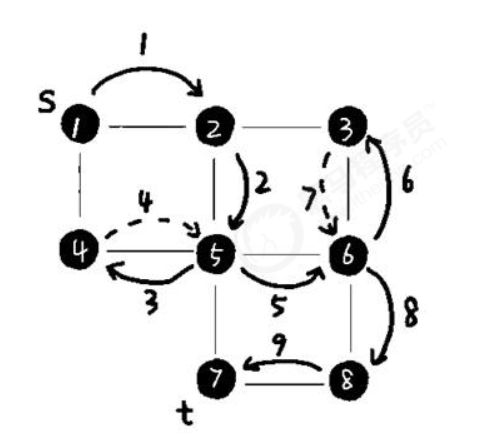
深度优先遍历 Depth-First-Search，DFS，是一种用于遍历或搜索树或图的算法。

算法流程：

1. 首先将根节点放入stack 中。
2. 从 stack 中取出第一个节点，并检验它是否为目标。如果找到所有的节点，则结束搜寻并回传结果。否则将它某一个尚未检验过的直接子节点加入stack中。
3. 重复步骤 2。
4. 如果不存在未检测过的直接子节点。将上一级节点加入stack中，重复步骤 2。
5. 重复步骤 4。
6. 若stack为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

这里的 stack 可以理解为自己实现的栈，也可以理解为调用栈。如果是调用栈的时候就是递归，如果是自己实现的栈的话就是迭代。

算法模版

一个典型的通用的 DFS 模板可能是这样的：

boolean[] visited;
void dfs(int i) {
    if (满足特定条件）{
        // 返回结果 or 退出搜索空间
    }
    visited[i] = true // 将当前状态标为已搜索
    for (根据i能到达的下个状态j) {
        if (!visited[j]) { // 如果状态j没有被搜索过
            dfs(j)
        }
    }
}

这部分内容在可以参考树专题与回溯算法内容

题目

752. 打开转盘锁

public int openLock(String[] deadends, String target) {
    // 记录需要跳过的死亡密码
    Set<String> deads = new HashSet<>();
    for(String s: deadends){
        deads.add(s);
    }
    // 记录已经穷举过的密码，防止走回头路
    Set<String> visited = new HashSet<>();
    // 队列
    Queue<String> queue = new LinkedList<>();
    // 从起点开始进行BFS
    int step = 0;
    queue.offer("0000");
    visited.add("0000");
    while(!queue.isEmpty()){
        // 当前层的节点数
        int size = queue.size();
        // 遍历当前层的所有节点数
        for(int i=0; i<size; i++){
            String cur = queue.poll();
            // 判断节点是否相应条件
            if(deads.contains(cur)) continue;
            if(cur.equals(target)) return step;
            // 周围的还未访问过的可能都加入队列中
            for(int j=0; j<4; j++){
                // 向上拨一个数字
                String up = plusOne(cur, j);
                if (!visited.contains(up)) {
                    queue.offer(up);
                    visited.add(up);
                }
                // 向下拨一个数字
                String down = minusOne(cur, j);
                if (!visited.contains(down)) {
                    queue.offer(down);
                    visited.add(down);
                }
            }
        }
        step += 1; // 遍历完一层，层数+1
    }
    // 如果穷举完都没找到目标密码，那就是找不到了
    return -1;
}
// 将 s[j] 向上拨动一次
private String plusOne(String s, int j) {
    char[] ch = s.toCharArray();
    if (ch[j] == '9')
        ch[j] = '0';
    else
        ch[j] += 1;
    return new String(ch);
}
// 将 s[i] 向下拨动一次
private String minusOne(String s, int j) {
    char[] ch = s.toCharArray();
    if (ch[j] == '0')
        ch[j] = '9';
    else
        ch[j] -= 1;
    return new String(ch);
}

参考：BFS 算法框架套路详解

773. 滑动谜题

public int slidingPuzzle(int[][] board) {
    /******* 准备工作 *******/
    int m = 2, n = 3;
    char[] start = new char[6];
    char[] target = {'1', '2', '3', '4', '5', '0'};
    // 将2*3转化为字符串
    int index_s = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            start[index_s++] = (char)(board[i][j] + '0');
        }
    }
    // 记录一维字符串的相邻索引
    List<List<Integer>> neighbor = new ArrayList<>();
    neighbor.add(Arrays.asList(1, 3));
    neighbor.add(Arrays.asList(0, 2, 4));
    neighbor.add(Arrays.asList(1, 5));
    neighbor.add(Arrays.asList(0, 4));
    neighbor.add(Arrays.asList(1, 3, 5));
    neighbor.add(Arrays.asList(2, 4));
    /******* BFS 算法框架开始 *******/
    Queue<char[]> queue = new LinkedList<>();
    Set<String> visited = new HashSet<>();
    queue.offer(start);
    visited.add(new String(start));
    int steps = 0;
    while(!queue.isEmpty()){
        int size = queue.size();
        for(int i=0; i<size; i++){
            char[] cur = queue.poll();
            // 判断是否达到目标局面
            if(isEqual(cur, target)){
                return steps;
            }
            // 找到数字 0 的索引
            int index = 0;
            for(; cur[index] != '0'; index++);
            // 将数字 0 和相邻的数字交换位置
            for(Integer adj: neighbor.get(index)){
                char[] tmp = new char[6];
                System.arraycopy(cur, 0, tmp, 0, 6);
                swap(tmp, index, adj);
                if(!visited.contains(new String(tmp))){
                    queue.offer(tmp);
                    visited.add(new String(tmp));
                }
            }
        }
        steps++;
    }
    return -1;
}
private void swap(char[] chars, int i, int j){
    char tmp = chars[i];
    chars[i] = chars[j];
    chars[j] = tmp;
}
private boolean isEqual(char[] a, char[] b){
    if(a.length != b.length){
        return false;
    }
    for(int i=0; i<a.length; i++){
        if(a[i] != b[i]){
            return false;
        }
    }
    return true;
}

参考：益智游戏克星：BFS暴力搜索算法

111. 二叉树的最小深度

public int minDepth(TreeNode root) {
    if(root == null){
        return 0;
    }
    return bfs(root);
}
private int bfs(TreeNode root){
    Queue<TreeNode> queue = new LinkedList<>();
    // 记录层数
    int steps = 1;
    queue.offer(root);
    while(!queue.isEmpty()){
        // 当前层的节点数
        int size = queue.size();
        // 遍历当前层的所有节点数
        for (int i=0; i<size; i++){
            TreeNode node = queue.poll();
            // 判断节点是否满足，而决定是否返回等操作
            if(node.left == null && node.right == null){
                return steps;
            }
            if(node.left != null){
                queue.offer(node.left);
            }
            if(node.right != null){
                queue.offer(node.right);
            }
        }
        steps += 1;
    }
    return steps;
}