DFS————从普及到IOI（暴力骗分小能手）

DFS

啦啦啦，再来水一波

先说思想吧！

背景：

深度优先搜索算法（英语：Depth-First-Search，简称DFS）是一种用于遍历或搜索树或图的算法。

————来自度娘

一、思想

DFS算法思想:一直往深处走,直到找到解或者走不下去为止

二、用途

由于时间复杂度过大一般不是正解，大部分情况是想不出题目正解，无奈之下写的暴力搜索或对拍时候用的，当然也有dfs的题，但是几乎不考。

三、实现过程

沿着树的深度遍历树的节点（不是树也没有关系啦，本蒟蒻图论菜的一批，依然学习了dfs），尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(n!)。

四、基本模版

int check() {
    if(满足条件)
        return 1;
    return 0;
}

void dfs(int step) {
    判断边界
    ｛
        相应操作
    ｝
    尝试每一种可能
    ｛
        满足check条件
        标记
        继续下一步dfs(step+1)
        恢复初始状态（回溯的时候要用到）
    ｝ 

会了模版，那就完结撒花了！

等等，显然我们并没有学会如何使用，那一起来看几个题目，熟悉一下。

四、题目（加深理解）

1、全排列问题

题目：给你n个字符串，把它们以此放入n个箱子中，输出全部排放方法。

思路：首先我们要检查箱子的状态（是否为空），将未放入的字符（未被标记的）放入，并进行标记

放入后要恢复到初始状态（回溯），到扫到了n+1个箱子时（边界处理），本次排列结束

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

int n，w;
char s[100],re[100];
bool vis[100];

void dfs(int step) {//step为第几步，即第几个箱子
    int i;//i为第i个字符
    if(step==n+1) {//判断边界
        for(i=1;i<=n;i++) printf("%c",re[i]);
        printf("\n");
        return ;
    }
    for(i=1;i<=n;i++) {//尝试每一种可能
        if(vis[i]==0) {//满足check条件 （即：判断字符是否被标记）
            vis[i]=1;//标记
            re[step]=s[i];
            dfs(step+1);//继续下一步dfs(step+1)
            vis[i]=0;//恢复初始状态（回溯）
        }
    }
    return ;
}

int main()
{
    scanf("%d",&w);
    for(int i=1;i<=n;i++){
        memset(s,0,sizeof(s));
        memset(vis,0,sizeof(vis));
        scanf("%s",s+1);
        n=strlen(s+1);
        dfs(1);
    }
    return 0;
}

2、Prime Ring Problem

题目：环由n个圆组成，如图所示。 将自然数1,2，...，n分别放入每个圆中，两个相邻圆中的数字之和应为素数。

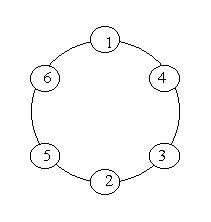
输入：n(0<n<20)

输出：输出格式如下所示。 每行代表环中的一系列圆圈数，从1开始顺时针和逆时针开始。 数字的顺序必须满足上述要求。 按字典顺序打印解决方案。

（输入时是要保证可以一直输入，看看代码就可以了）

样例：

思路：此题思路与全排列思路差不多，只是判断条件比较多，我们需要判断相邻两数之和是否为素数（注意最后一个字符会与1相加进行判断）

代码出来吧（皮卡丘）！

//Prime Ring Problem
#include<bits/stdc++.h>

using namespace std;

int book[100],result[100],n;

int prime(int n) {//判断是否为素数
    if(n<=1) return 0;
    int i;
    for(i=2;i*i<=n;i++) {
        if(n%i==0) break;
    }
    if(i*i>n) return 1;
    return 0;
}

int check(int i,int step) {// 判断当前数字(i)是否能放入此位置 (step)
    if(book[i]==0&&prime(i+result[step-1])) {//此位置未被标记，且与前一个数的和为素数
        if(step==n-1) {//判断是否是最后一步
            if(!prime(i+result[0])) return 0;//判断最后一步与1的和是否为素数
        }
        return 1;
    }
    return 0;
}

void dfs(int step) {
    if(step==n) {//边界处理
        for(int a=0;a<n;a++)
        printf("%d ",result[a]);
        printf("\n");
        return ;
    }
    int i=2;
    for(i=2;i<=n;i++) {
        if(check(i,step)) {//满足check条件
            book[i]=1;//标记
            result[step]=i;
            dfs(step+1);//继续下一步dfs(step+1)
            book[i]=0;//恢复初始状态（回溯）
        }
    }
    return ;
}

int main()
{
    int num=0;
    while(scanf("%d",&n)){//一直输入
        num++;
        memset(result,0,sizeof(result));
        memset(book,0,sizeof(book));
        result[0]=1;
        printf("Case %d:\n",num);
        dfs(1);
        printf("\n");
    }
    return 0;
}

2019-07-12

3、油田问题（A - Oil Deposits ）

题目：输入多个n行m列的矩阵，用00表示输入结束。找出有多少块石油区域，用“@”代表石油，假如两个“@”在横，竖或对角线上相邻（上，下，左，右，左上，左下，右上，右下），就说它们位于同一区域，对于每个输入，输出一个数表示有几个石油区域。

输入：n(1<=n<=100) m(1<=m<=100)

输出：对于每一个矩形区域，输出油藏的数量。

样例输入：

1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

样例输出：

0
1
2
2

思路：这个题其实比上一题简单，放在这里可能是因为它比较脱离模版（显然别人是这么排的），思路其实很简单了，若是求有多少块油（即：有多少@），扫一遍就好了，但题目要求，相邻的是同一个区域，求多少个区域，那就扫到每个油田我们都把与它相邻的八个点都扫一遍（若扫到的相邻的点也是油田，那就同样把他的相邻点也扫了，只记一次），注意的是扫到油田时，要将它标记并不将它恢复（回溯），否则我们将陷入死循环。 ( What? Why? ) 我们思考一下，当扫到一个油田（A）我们扫与它相邻的点，若其中还有油田（B），油田（A）也同样是与油田（B）相邻的，我们还要重新扫到油田（A），从而陷入死循环，所以我们不能回溯。

上代码！

//A - Oil Deposits
#include<bits/stdc++.h>

using namespace std;

char a[105][105];
char dir[8][2]={{1,0},{-1,0},{1,1},{-1,-1},{0,1},{0,-1},{1,-1},{-1,1}};
int n,m,result;

int check(int x,int y) {//检查是否有石油（@）
    if(x>=0&&x<=n&&y>=0&&y<=m&&a[x][y]=='@')
        return 1;
    return 0;
}

int dfs(int x,int y) {
    int i,xx,yy;
    if(check(x,y)) {
        a[x][y]='.';// 将找到的油田标记，不用恢复，会重复陷入死循环
        for(i=0;i<8;i++) {//检查相邻的八个方向，若有油，将它标记，继续便利它的相邻方向 ，防止重复记录
            xx=x+dir[i][0];
            yy=y+dir[i][1];
            dfs(xx,yy);
        }
        return 1;
    }
    return 0;
}

int main()
{
    while(scanf("%d%d",&n,&m)) {
        if(n==0||m==0) break;
        result=0;
        memset(a,0,sizeof(a));
        for(int i=1;i<=n;i++)
            scanf("%s",&a[i]);
        for(int i=1;i<=n;i++) {//对每个点都进行搜索
            for(int j=0;j<m;j++) {
                if(dfs(i,j)) result++;//若发现油田结果+1
            }
        }
        printf("%d\n",result);
    }
    return 0;
}

4、棋盘问题

题目：在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案C。

输入：输入含有多组测试数据。 每组数据的第一行是两个正整数，n k，用一个空格隔开，表示了将在一个n*n的矩阵内描述棋盘，以及摆放棋子的数目。 n <= 8 , k <= n 当为-1 -1时表示输入结束。 随后的n行描述了棋盘的形状：每行有n个字符，其中 ‘#’ 表示棋盘区域， ‘.’表示空白区域。

输出：对于每一组数据，给出一行输出，输出摆放的方案数目C （数据保证C<2^31）。

样例输入：

2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1
样例输出：

2
1

是不是很简单呐，没错，你已经掌握了dfs（深搜）的思路了，所以要先自己想一下，试着写一下代码，再看思路，题目很简单的。

思路：是不是都已经想出来了呢？（显然都已经A了）。只需要枚举每个棋子的位置，我们每次将一行放入棋子，放下一枚棋子时就在下一行放，用dir[]对放入的列进行标记，方便判断此列是否有放过棋子，就ok了。

代码！代码！麻利哄！

#include<bits/stdc++.h>

using namespace std;

int n,k,ans;
char a[105][105];
int dir[105];

void dfs(int h,int k) {
    if(k==0) {//边界处理，若棋子放完，方案数+1
        ans++;
        return ;
    }
    for(int i=h;i<n;i++) {//每次都从下一行开始搜避免了重复
        for(int j=0;j<n;j++) {
            if(a[i][j]=='.'||dir[j]==1)  continue;//dir[j]表示此列是否已经被占有
            dir[j]=1;//标记
            dfs(i+1,k-1);//搜下一行，棋子数量减少1
            dir[j]=0;//恢复初始状态（回溯）
        }
    }
}

int main()
{
    while(scanf("%d%d",&n,&k)) {
        if(n==-1&&k==-1) break;
        ans=0;
        memset(a,0,sizeof(a));
        memset(dir,0,sizeof(dir));
        for(int i=0;i<n;i++) {
            scanf("%s",a[i]);
        }
        dfs(0,k);//在第0行放第k个棋子
        printf("%d\n",ans);
    }
    return 0;
}

（哇！我会深搜了！）是的，基本模版你已经掌握了，但是搜索是很考验代码能力的，所以需要勤加练习，多做题，增强码力！