面试题68 - II. 二叉树的最近公共祖先

<搜索树结点>

<获取路径>

题目描述

---

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

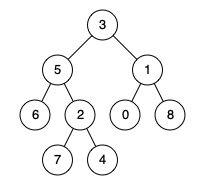
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

注意：本题与主站 236 题相同：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/

我的思路

---

1. 定义 dfs(self , node , tar , path) 为在树中找到目标结点（tar），并储存从根结点到目标结点的路径（path）

2. 找到结点 p 的路径 path_p ，结点 q 的路径 path_q

3. 从尾到头比较路径 path_p 、 path_q，返回相等的那个结点

* 一定会有相同的结点，最坏的情况相同的结点是根结点

class Solution(object):
    def __init__(self):
        self.ret = 0
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        path_p,path_q = [],[]
        self.dfs(root,p,path_p)
        self.dfs(root,q,path_q)
        ls = min(len(path_p),len(path_q))-1
 
        while ls>=0:
            if path_p[ls] == path_q[ls]:
                return path_p[ls]
            ls-=1
 
    def dfs(self,root,tar,path):
        if not root:
            return False
 
        path.append(root.val)
 
        if root.val == tar.val:
            return True
        ans1 = self.dfs(root.left,tar,path)
        ans2 = self.dfs(root.right,tar,path)
        # 搜到叶子节点，没找到，则原路返回，把路上的结点pop出去
        if not ans1 and not ans2:
            path.pop()
        return ans1 or ans2

总结

---

1. 在一棵树中搜索目标结点

2. 深搜获取根节点到目标结点的路径