Probabilistic Principal Component Analysis

引
主要内容
- EM算法求解
附录
- 极大似然估计
代码

Tipping M E, Bishop C M. Probabilistic Principal Component Analysis[J]. Journal of The Royal Statistical Society Series B-statistical Methodology, 1999, 61(3): 611-622.

引

PPCA 通过高斯过程给出了普通PCA一个概率解释，这是很有意义的。论文还利用PPCA进行缺失数据等方面的处理（不过这方面主要归功于高斯过程吧）。

\[t = Wx + \mu + \epsilon
\]

其中$t \in \mathbb{R}^d$为观测变量，也就是样本，而$x \in \mathbb{R}^q$是隐变量，$W \in \mathbb{R}^{d \times q}$将$x,t$二者联系起来。另外，$\epsilon$是噪声。

令$S = \frac{1}{N} \sum \limits_{n=1}^N (t_n -\mu )(t_n - \mu)^T$是样本协方差矩阵，其中$\mu$是样本均值。论文的主要工作，就是将$S$的列空间和$W$联系起来。

主要内容

假设$\epsilon \sim N(0, \sigma^2 I)$,$\: x \sim N(0, I)$，二者独立。那么，容易知道$t$在$x$已知的情况下的条件概率为：

\[t|x \sim N(Wx + \mu, \sigma^2I)
\]

然后论文指出，通过其可求得$t$的边际分布：

\[t \sim N(\mu, C)
\]

其中$C = WW^T + \sigma^2 I$。这个证明，在贝叶斯优化中有提过，不过我发现，因为$t=Wx+\mu + \epsilon$，是服从正态分布随机变量的线性组合，所以$t$也服从正态分布，所以通过$E(t)$和$E((t-E(t))(t-E(t))^T)$也可以得到$t$的分布。

其似然函数$L$为：

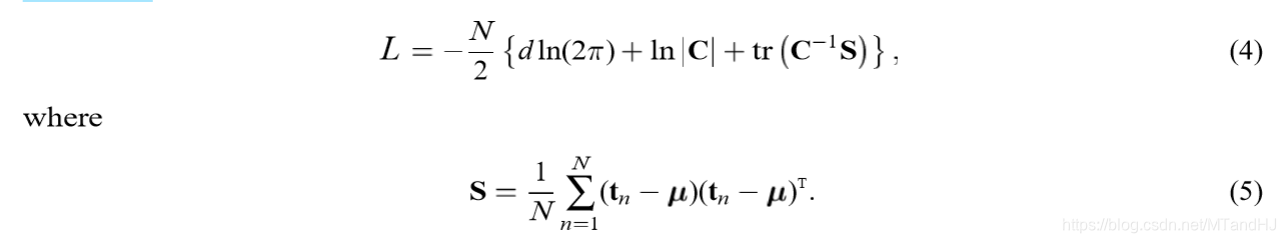
将$W，\sigma$视为参数，我们可以得到其极大似然估计：

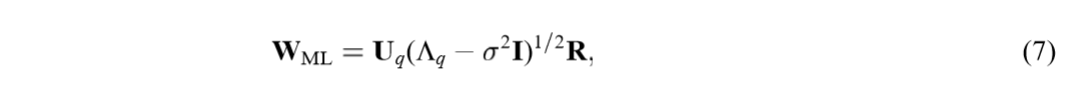
其中$U_{q}$的列是$S$的主特征向量，而$\Lambda_q$的对角线元素为特征向量对应的特征值$\lambda_1, \ldots, \lambda_q$（为所有特征值的前$q$个，否则$W$将成为鞍点），$R \in \mathbb{R}^{q \times q}$是一个旋转矩阵。注意到，$W_{ML}$的列向量并不一定正交。

这部分的推导见附录。

同样的，我们可以推导出，$x$在$t$已知的情况下的条件分布：

\[x|t \sim N(M^{-1}W^T(t-\mu),\sigma^2 M^{-1}
\]

其中$M = W^TW+\sigma^2I$

这个推导需要利用贝叶斯公式：

\[p(x|t) = \frac{p(t|x)p(t)}{p(t)}
\]

为什么要提及这个东西，因为可以引出一个很有趣的性质，注意到$x|t$的均值为：

\[M^{-1}W^T(t-u)
\]

令$W = W_{ML}$,且假设$\sigma^2 \rightarrow 0$，那么均值就成为：

\[(W_{ML}^TW_{ML})^{-1}W_{ML}^T(t-u)
\]

实际上就是$(t-u)$在主成分载荷向量上的正交投影，当然这里不要计较$W_{ML}^TW_{ML}$是否可逆。这就又将PPCA与普通的PCA联系在了一起。

EM算法求解

论文给出了$W$的显式解（虽然有点地方不是很明白），也给出了如何利用EM算法来求解。

构造似然估计：

对$x_n$求条件期望（条件概率为$p(x_n|t_n,W,\sigma^2)$）：

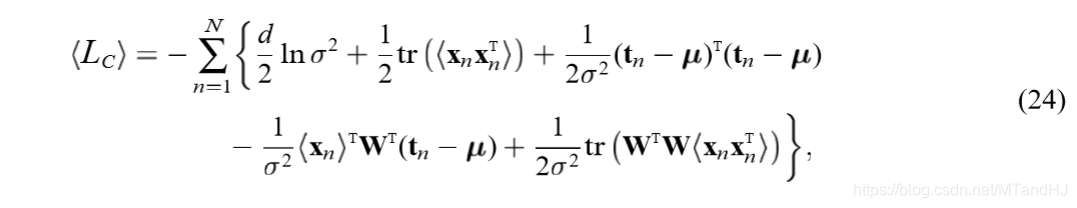
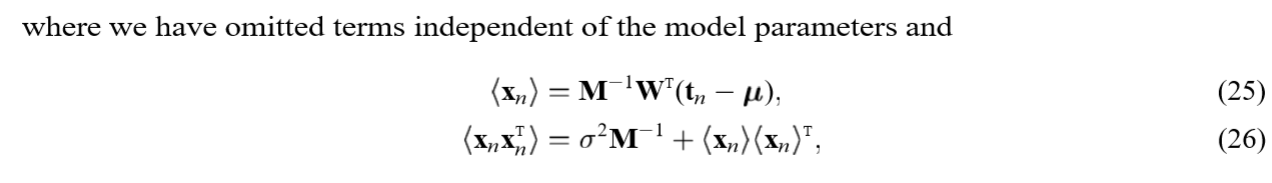
$M$步是对上述$W,\sigma$求极大值，注意$<\cdot>$里面的$M, \sigma$是已知的（实际上，用$M', \sigma'$来表述更加合适）：

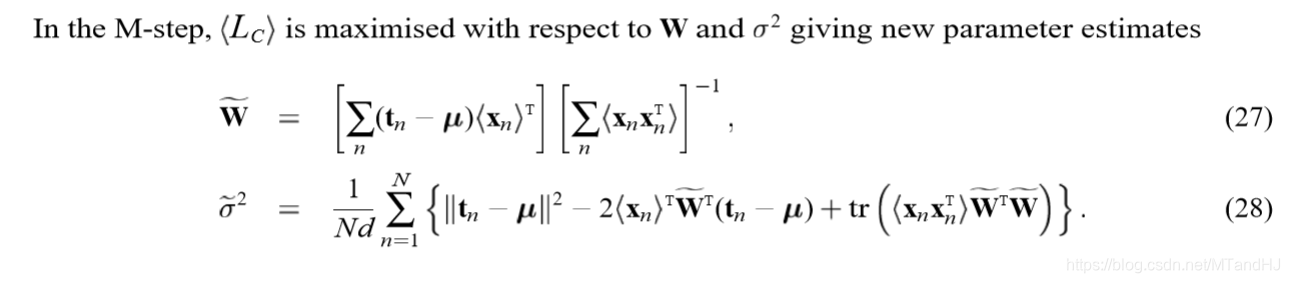
有更加简练的表述形式：

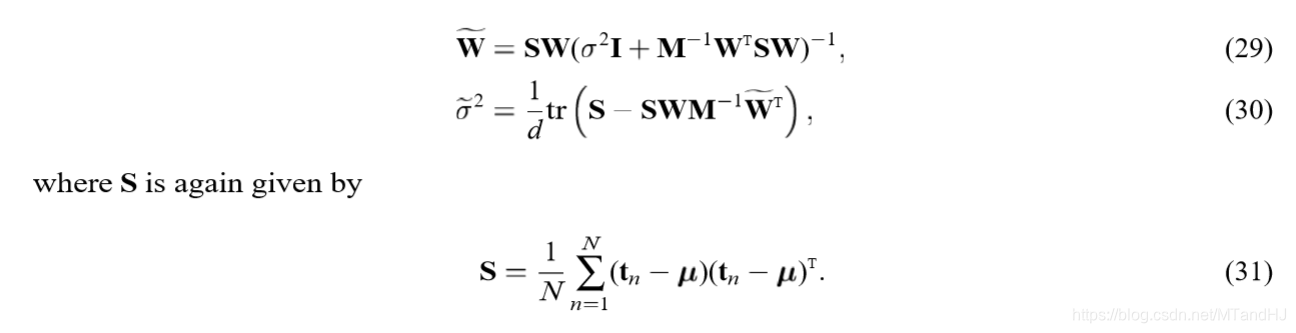
符号虽然多，但是推导并不麻烦，自己推导的时候并没有花多大工夫。

附录

极大似然估计

已知对数似然函数为：

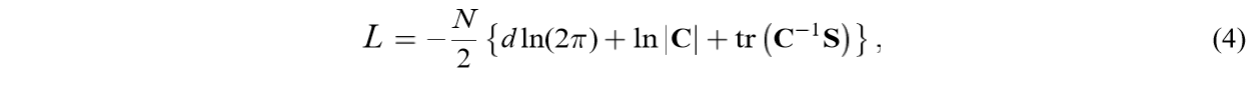
先考察对$W$的微分：

\[\begin{array}{ll}
\mathrm{d}L = -\frac{N}{2}\{\frac{\mathrm{d}|C|}{|C|} + \mathrm{dtr}(C^{-1}S)\}
\end{array}
\]

\[\begin{array}{ll}
\frac{\mathrm{d}|C|}{|C|}
&= \mathrm{tr}(C^{-1}\mathrm{d}C) \\
&= \mathrm{tr}[C^{-1}(\mathrm{d}WW^T+W\mathrm{d}W^T)] \\
&= 2\mathrm{tr}[W^TC^{-1}\mathrm{d}W] \\
\end{array}
\]

\[\begin{array}{ll}
\mathrm{dtr}(C^{-1}S)
&= \mathrm{tr}(\mathrm{d}C^{-1}S) \\
&= -\mathrm{tr}(C^{-1}[\mathrm{d}C]C^{-1}S) \\
&= -\mathrm{tr}(C^{-1}SC^{-1}\mathrm{d}C) \\
&= -2\mathrm{tr}(W^TC^{-1}SC^{-1}\mathrm{d}W) \\
\end{array}
\]

所以，要想取得极值，需满足：

\[C^{-1}W = C^{-1}SC^{-1}W \\
\Rightarrow \quad SC^{-1}W=W
\]

论文说这个方程有三种解：

$W=0$，0解，此时对数似然函数取得最小值（虽然我没看出来）。
$C=S$:

\[WW^T + \sigma^2 I = S \\
\Rightarrow WW^T = S-\sigma^2
\]

其解为：

\[W = U_{S} (\Lambda_S-\sigma^2I)^{1/2}R
\]

其中$S = U_S \Lambda U_S^T$。

第三种，也是最有趣的解，$SC^{-1}W=W$但是$W \ne 0, C \ne S$。假设$W=ULV^T$,其中$U \in \mathbb{R}^{d \times q}$, $L \in \mathbb{R}^{q \times q}$为对角矩阵，$V \in \mathbb{R}^{q \times q}$。通过一系列的变换(我没有把握能完成这部分证明，感觉好像是对的)，可以得到：

\[SUL = U(\sigma^2L+L^2)L
\]

于是$Su_j = (\sigma^2I + l_j^2)u_j$，其中$u_j$为$U$的第j列，$l_j$为$L$的第j个对角线元素。因此，$u_j$就成了$S$的对应特征值$\lambda_j = \sigma^2 + l_j^2$的特征向量（注意到这个特征值是必须大于等于$\sigma^2$）。于是，有：

\[W = U_q(K_q-\sigma^2I)^{1/2}R
\]

其中：

\[k_j = \left \{
\begin{array}{ll}
\lambda_j & 对应特征值u_j \\
\sigma^2
\end{array} \right .
\]

实际上就是$k_j=\lambda_j$

注意，上面的分析只能说明其为驻定解，事实上$U_q$只说明了其为$S$的特征向量，而没有限定是哪些特征向量。

将解$W = U_q(K_q-\sigma^2I)^{1/2}R$代入对数似然函数可得（$C = WW^T+\sigma^2 I$）：

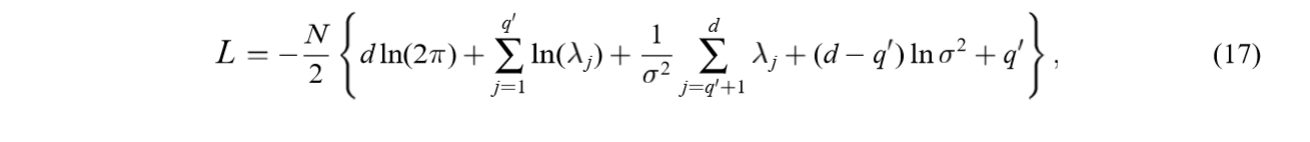
其中$q'$是非零$l_1,\ldots,l_{q'}$的个数。

上面的是蛮好证明的，注意$\{\cdot\}$中第2项和第4项和为$\ln |C|$，第3，5项构成$\mathrm{tr}(C^{-1}S)$。

对$\sigma$求极值，可得：

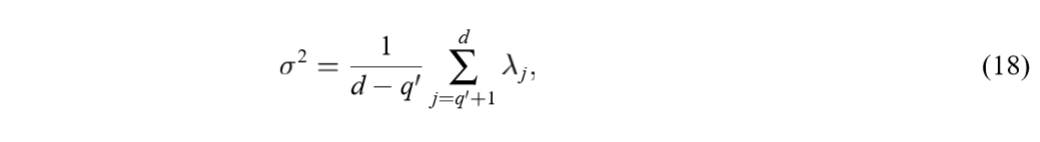
且是极大值，因为显然$\sigma \rightarrow 0$会导致$L \rightarrow - \infty$。代入原式可得：

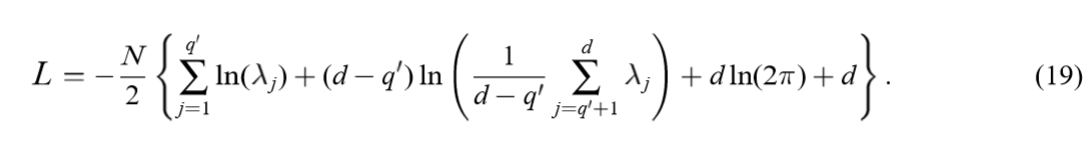
最大化上式等价于最小化下式：

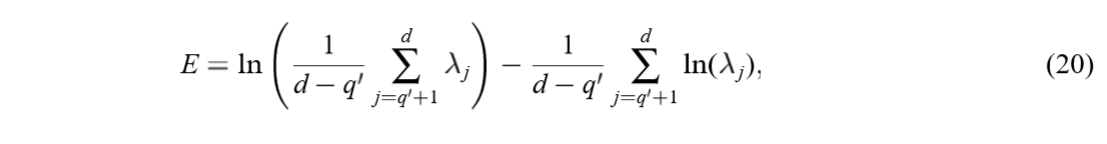
注意到，上式只与被舍弃的$l_j=0$的$\lambda_j$有关，又$\lambda_i \ge \sigma^2, i=1,\ldots, q$，再结合(18)，可以知道最小的特征值一定是被舍弃的。但是论文说，应当是最小的$d-q'$个特征值作为被舍弃的（因为这些特征值必须在一块？）。

仔细想来，似然函数可以写成：

\[L = -\frac{N}{2} \{d \ln (2\pi) + \sum \limits_{j=1}^q \ln (\lambda_j) + \frac{1}{\sigma^2}\sum \limits_{j=q+1}^d \lambda_j + (d-q)\ln (\sigma^2) + q\}
\]

好吧，还是不知道该如何证明。

代码

"""

瞎写的，测试结果很诡异啊

"""

import numpy as np

class PPCA:

    def __init__(self, data, q):

        self.__data = np.array(data, dtype=float)

        self.__n, self.__p = data.shape

        self.__mean = np.mean(self.data, 0)

        self.q = q

        assert q < self.__p, "Invalid q"

    @property

    def data(self):

        return self.__data

    @property

    def n(self):

        return self.__n

    @property

    def p(self):

        return self.__p

    def explicit(self):

        data = self.data - self.__mean

        S = data.T @ data / self.n

        value, vector = np.linalg.eig(S)

        U = vector[:, :self.q]

        sigma = np.mean(value[self.q:])

        newvalue = value[:self.q] - sigma

        return U * newvalue

    def EM(self):

        data = self.data - self.__mean

        S = data.T @ data / self.n

        W_old = np.random.randn(self.p, self.q)

        sigma = np.random.randn()

        count = 0

        while True:

            count += 1

            M = W_old.T @ W_old + sigma

            M_inv = np.linalg.inv(M)

            W_new = S @ W_old @ np.linalg.inv(sigma + M_inv @ W_old.T @ S @ W_old)

            sigma_new = np.trace(S - S @ W_old @ M_inv @ W_new.T) / self.p

            if np.sum(np.abs(W_new - W_old)) / np.sum(np.abs(W_old)) < 1e-13 and \

                np.abs(sigma_new - sigma) < 1e-13:

                return W_new

            else:

                W_old = W_new

                sigma = sigma_new