Geometric GAN

目录

• 概
• 主要内容
  • McGAN
  • 结合SVM
    • 训练
    • 训练
  • 理论分析
    • 证明

Jae Hyun Lim, Jong Chul Ye, Geometric GAN.

概

很有趣, GAN的训练过程可以分成

1. 寻找一个超平面区分real和fake;
2. 训练判别器, 使得real和fake分得更开;
3. 训练生成器, 使得real趋向错分一侧.

主要内容

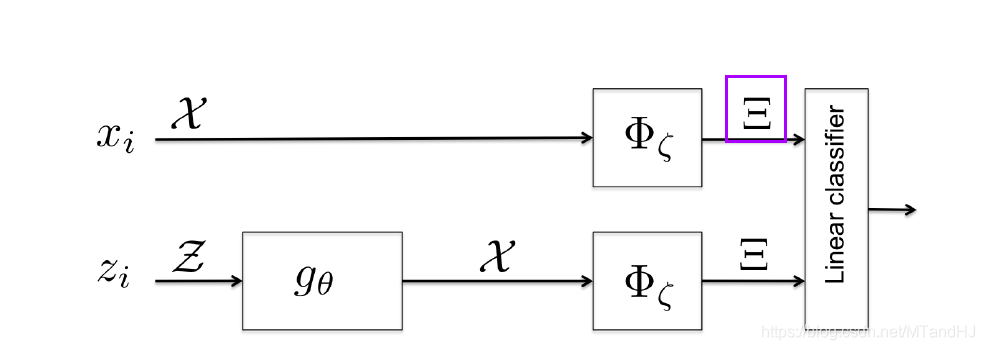
McGAN

本文启发自McGAN, 在此基础上, 有了下文.

结合SVM

设想, GAN的判别器\(D(x) = S(\langle w, \Phi_{\zeta}(x) \rangle)\), 其中\(S\)是一个激活函数, 常见如sigmoid, 先假设其为identity(即\(D(x)=\langle w, \Phi_{\zeta}(x) \rangle\)).

McGAN 是借助\(\langle w, \Phi_{\zeta}(x)\rangle\)来构建IPM, 并通过此来训练GAN. 但是，注意到， 若将\(\Phi_{\zeta}(x)\)视作从\(x\)中提取出来的特征, 则\(\langle w, \Phi_{\zeta}(x)\rangle\)便是利用线性分类器进行分类，那么很自然地可以将SVM引入其中(训练判别器的过程.

\[\begin{array}{rcl}
\min_{w, b} & \frac{1}{2} \|w\|^2 + C \sum_i (\xi_i + \xi_i') & \\
\mathrm{subject \: to} & \langle w, \Phi_{\zeta}(x_i) \rangle + b \ge 1-\xi_i & i=1,\ldots, n\\
& \langle w, \Phi_{\zeta}(g_{\theta}(z_i)) \rangle + b \le \xi_i'-1 & i=1,\ldots,n \\
& \xi_i, \xi_i' \ge 0, \: i=1,\ldots,n.
\end{array}
\]

类似于

\[\tag{13}
\min_{w,b} \: R_{\theta}(w,b;\zeta),
\]

其中

\[\tag{14}
\begin{array}{ll}
R_{\theta}(w,b;\zeta) =
& \frac{1}{2C n} \|w\|^2 + \frac{1}{n} \sum_{i=1}^n \max (0, 1-\langle w, \Phi_{\zeta} (x_i) \rangle -b) \\
& + \frac{1}{n} \sum_{i=1}^n \max (0, 1+ \langle w, \Phi_{\zeta}(g_{\theta}(z_i))\rangle+b).
\end{array}
\]

进一步地， 用以训练\(\zeta\):

\[\tag{15}
\min_{w,b,\zeta} \: R_{\theta}(w,b;\zeta).
\]

SVM关于\(w\)有如下最优解

\[w^{SVM} := \sum_{i=1}^n \alpha_i \Phi_{\zeta}(x_i) - \sum_{i=1}^n \beta_i \Phi_{\zeta} (g_{\theta}(z_i)),
\]

其中\(\alpha_i, \beta_i\)只有对支持向量非零.

定义

\[\mathcal{M} = \{\phi \in \Xi | |\langle w^{SVM}, \phi \rangle + b | \le 1\}
\]

为margin上及其内部区域的点.

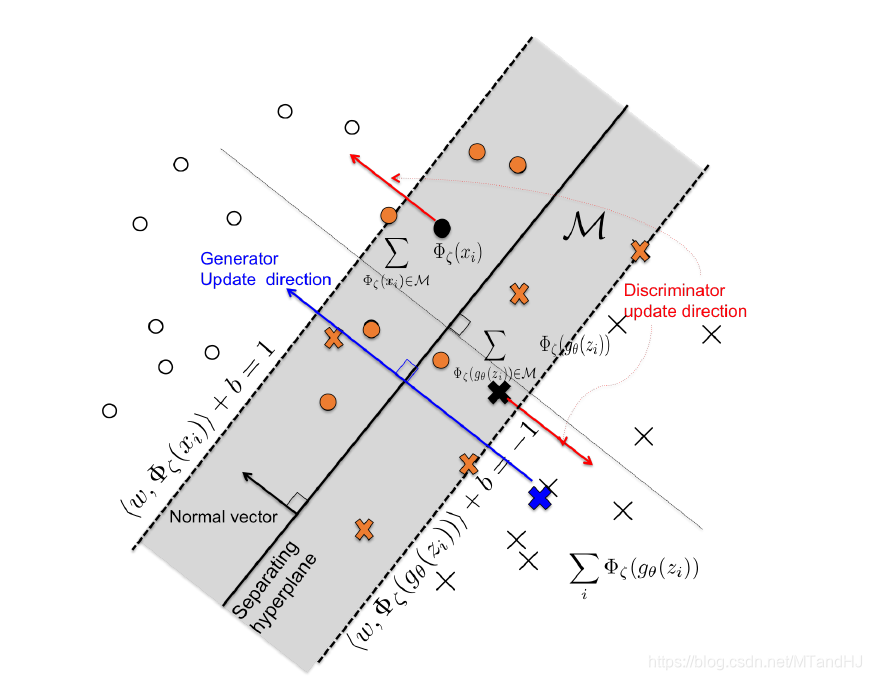
于是

\[\tag{18}
\begin{array}{ll}
R_{\theta}(w,b;\zeta) = \frac{1}{n} \sum_{i=1}^n \langle w^{SVM}, s_i \Phi_{\zeta} (g_{\theta}(z_i))-t_i \Phi_{\zeta}(x_i) \rangle + \mathrm{constant},
\end{array}
\]

其中

\[\tag{19}
t_i =
\left \{ \begin{array}{ll}
1, & \Phi_{\zeta}(x_i) \in \mathcal{M} \\
0, & \mathrm{otherwise}
\end{array} \right. , \quad
s_i =
\left \{ \begin{array}{ll}
1, & \Phi_{\zeta}(g_{\theta}(z_i)) \in \mathcal{M}\\
0, & \mathrm{otherwise}.
\end{array} \right.
\]

训练\(\zeta\)

于是\(\zeta\)由此来训练

\[\zeta \leftarrow \zeta +\eta \frac{1}{n} \sum_{i=1}^n \langle w^{SVM}, t_i \nabla_{\zeta} \Phi_{\zeta}(x_i) - s_i \nabla_{\zeta}\Phi_{\zeta} (g_{\theta}(z_i)) \rangle .
\]

训练\(g_{\theta}\)

就是固定\(w,b,\zeta\)训练\(\theta\).

所以

\[\min_{\theta} \: L_{w, b, \zeta}(\theta),
\]

其中

\[L_{w,b,\zeta}(\theta)= -\frac{1}{n} \sum_{i=1}^n D(g_{\theta}(z_i)),
\]

的

\[\theta \leftarrow \theta+\eta \frac{1}{n} \sum_{i=1}^n \langle w^{SVM}, s_i \nabla_{\theta}\Phi_{\zeta} (g_{\theta}(z_i)) \rangle .
\]

理论分析

\(n \rightarrow \infty\)的时候

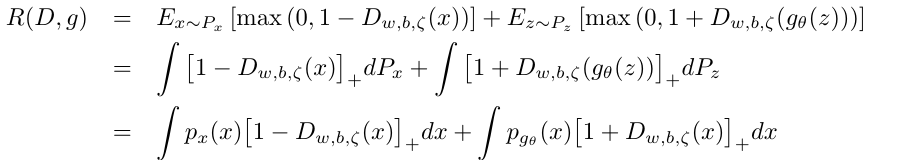
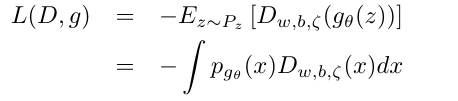
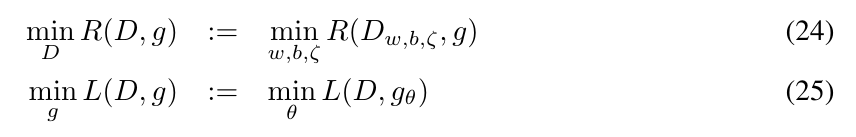
定理1： 假设\((D^*,g^*)\)是(24), (25)交替最小化解, 则\(p_{g^*}(x)=p_x(x)\)几乎处处成立, 此时\(R(D^*,G^*）=2\).

注: 假体最小化是指在固定\(g^*\)下, \(R(D^*,g^*)\)最小，在固定\(D^*\)下\(L(D^*,g^*)\)最小.

证明

注：文中附录分析了各种GAN的超平面分割解释, 挺有意思的.