关于dp那些事

拿到一道题，先写出状态转移方程，再优化时间复杂度

状态优化：

对于状态可累加

\(e.g.dp[i+j]=dp[i]+dp[j]+i+j\)

的，用倍增优化

决策优化：

\(e.g.dp[i][j]=\max(dp[i-1][j-233]+(j-233)^2,dp[i-1][j-232]+(j-232)^2,...,dp[i-1][j]+j^2)\)

单调队列优化

\(e.g.dp[i]=\max(dp[1]+i,dp[2]+2i,...,dp[i-1]+(i-1)i)\)

斜率优化

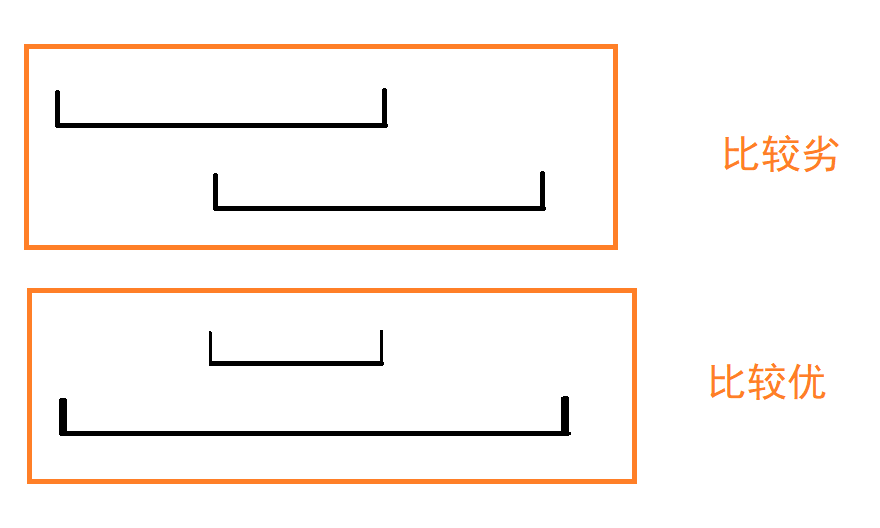
交叉小于包含

\(e.g.dp[i][j]=\max(dp[i][i]+dp[i+1][j],dp[i][i+1]+dp[i+2][j],...,dp[i][j-1]+dp[j-1][j],dp[i][j]+dp[j][j])\)

用四边形不等式优化